1 семестр - Башкирский институт физической культуры

Уральский государственный университет физической культуры
Башкирский институт физической культуры
Кафедра естественно-научных дисциплин
Вопросы к контрольной работе по математике 1 курс (1 семестр)
Специальность 100103 «Социально-культурный сервис и туризм» заочное отделение (2010-2011
уч.год).
Пояснение: в контрольной работе должны быть полностью раскрыты 2
теоретических вопроса (см. таблицу) и выполнены 4 задания. Номер варианта соответствует
вашему порядковому номеру в журнале. На первой странице или на форзаце работы вписать
обязательно номер варианта и полные формулировки всех вопросов. В конце работы
обязательно правильно указать использованную литературу.
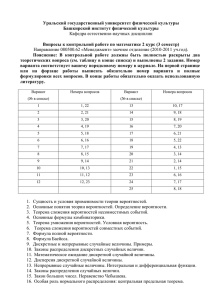
Вариант
(№ в списке)
1
2
3
4
5
6
7
8
9
10
11
12
13
Номера вопросов
1, 14
2, 15
3, 16
4, 17
5, 18
6, 19
7, 20
8, 21
9, 22
10, 23
11, 24
12, 21
13, 20
Вариант
(№ в списке)
14
15
16
17
18
19
20
21
22
23
24
25
26
Номера вопросов
14, 12
15, 11
16, 10
17, 9
18, 8
19, 7
20, 6
21. 5
22, 4
23, 3
24, 2
27, 1
18, 4
Вопросы:
1. Метод координат на плоскости.
2. Прямая. Уравнение прямой с угловым коэффициентом. Уравнение прямой в отрезках. Общее
уравнение прямой.
3. Кривые второго порядка.
4. Определители второго и третьего порядка и системы линейных уравнений с двумя и тремя
неизвестными.
5. Линейные пространства. Подпространства. Линейные преобразования. Евклидово
пространство.
6. Предел числовой последовательности. Предел функции.
7. Непрерывность функции. Основные свойства и теоремы непрерывных функций.
8. Производная функции. Ее геометрический смысл.
9. Дифференциал функции. Основные теоремы о дифференцируемых функциях.
10. Выпуклость функции. Максимальное и минимальное значение функции.
11. Неопределенный интервал.
12. Несобственные интегралы.
13. Основные методы интегрирования.
14. Понятие определенного интеграла. Приближенное вычисление определенного интеграла.
15. Производные и дифференциалы функций нескольких переменных.
16. Ряды. Числовые и функциональные ряды. Ряд Тейлора.
17. Дифференциальные уравнения первого порядка, их частные случаи первого порядка, их
частные случаи.
18. Линейные дифференциальные уравнения второго порядка.
19. Событие и вероятность. Основные теоремы теории вероятности.
20. Дискретные и непрерывные случайные величины. Математическое ожидание и дисперсия.
21. Нормальный закон распределения непрерывной случайной величины. Интеграл Лапласа.
22. Генеральная совокупность и выборка. Оценки параметров генеральной совокупности по ее
выборке.
23. Проверка статистических гипотез.
24. Линейная корреляция.
Задание 1
А) Вычислить неопределенный интеграл
1.
 { sin( kx)+ cos (mx)+ x n + n x}dx
2.
 { ln (xk+3)+ tg (mx)+ x k + k n}dx
Б) Вычислить определенный интеграл в диапазоне изменения аргумента х от 0 до 1
3.
 { x(kx)+ mxn - kx}dx
4.
 { ekx+ cos (mx)+ 2k + mn}dx
№
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
Вместо букв k, m, n подставить в примеры соответствующие числа
k
m
n
№
k
m
1
2
0,5
-1
2
25.
0,5
4
1
0,5
4
26.
-2
1
-3
-2
1
27.
1
2
1
1
2
28.
-3
0,5
-1
3
0,5
29.
0,5
4
2
0,5
4
30.
1
5
1
1
5
31.
1
1
0,5
1
1
32.
1
0,5
1
1
0,5
33.
4
1
-2
4
1
34.
6
0,5
1
6
0,5
35.
4
0,5
1
4
0,5
36.
0,5
0,5
0,5
0,5
0,5
37.
1
3
-1
1
3
38.
1
1
2
1
1
39.
2
2
2
2
2
40.
3
2
0,5
3
2
41.
3
3
-3
3
3
42.
4
0,5
2
4
0,5
43.
0,5
0.5
-0.5
0,5
0.5
44.
-1
2
-1
-1
2
45.
1
-1
-0,5
1
-1
46.
-2
1
-2
-2
1
47.
0,5
2
-0,5
0,5
2
48.
А) Вычислить производные:
1. y= ln(2xm +2xn)
2. y= cos(mx) * sin(nx)
3. Z = sin (cos(x+2m)) + 5xn
4. Z = sin(2xk) + ln(xn)
Задание 2
Б) Найти частные производные:
1. Z = cos(kx) * (3y)
5. Z = ( xk +3ym +7n)
2. Z = kyn+ xk
6. Z = 2y+ cos (yx)
3. Z = sin(2xn) + ln(xnym)
7. Z = y xn +ym
4. Z = cos(3x) + sin(2y)
8. Z = 2yk+ yxm
Вместо букв k, m, n подставить в примеры соответствующие числа
n
0,5
1
-3
1
-1
2
1
0,5
1
-2
1
1
0,5
-1
2
2
0,5
-3
2
-0.5
-1
-0,5
-2
-0,5
№
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
k
2
3
1
0,2
1,5
3
1
0
1
3
2
2
1
2
0,5
1
m
1
0.5
1,5
-1
1
0
2
-1
1
2
3
-1
0,5
1
2
2
n
2
3
2
3
1
2
1
5
1
1
4
1
2
3
1
2
№
21
22
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
k
2
2
1
2
3
2
5
1
3
1
4
3
2
1
2
2
m
0
2
-2
2
0
2
-1
1
0
1
-1
1
-2
-1
0,5
-1
n
2
2
2
2
2
2
1
1
1
4
1
1
1
4
2
1
17.
18.
19.
20.
2
1
1
3
1,5
2
1
3
3
2
2
1
37.
38.
39.
40.
Задание 3
1
2
3
1
-0,5
1,5
2
1,5
2
4
2
4
Вычислить определители матриц А и B.
Найти матрицы
1. D=А Ат
2. C=A3+ B
3. C1=AB2
4. C2=A2B
5. C3=AB-BA
1 k 0
где
№
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
A
m 1 b
a n 2
,
B
a 2 3
0 b 1
1 m n
Вместо букв a, b, k, m, n подставить в примеры соответствующие числа
a
b
k
n
m
№
a
b
k
n
1
-4
1
0
1
21
5
1
3
4
4
-2
3
1
0
22.
0
1
-4
2
0
1
2
-3
2
23.
6
0
-3
3
3
0
3
3
1
24.
1
-1
1
0
2
-1
1
2
-1
25.
1
5
3
1
-5
1
0
4
0
26.
2
0
9
0
0
1
3
1
2
27.
1
1
1
1
2
-0,5
3
3
1
28.
1
0
-2
-2
1
0
-1
0,5
1
29.
1
-2
-1
3
1
2
3
1
0,5
30.
0
1
-2
4
0,5
1
1
1
2
31.
1
1
-4
2
1
0,5
3
3
1
32.
0
1
-2
-2
0,5
3
1
2
1
33.
1
-1
1
2
5
1
3
4
0,5
34.
1
4
-2
0
0,5
1
-3
1
2
35.
2
-1
-1
0
m
0
-2
-1
1
0
0
1
1
1
1
-2
-1
1
1
1
16.
17.
18.
19.
20.
2
1
0
1
2
0
4
3
0,5
1
3
3
-1
2
-2
2
3
6
4
2
1
1
1
1
-1
36.
37.
38.
39.
40.
1
2
1
1
2
1
1
-1
-2
1
1
0
1
0
1
2
1
-1
1
-2
1
1
1
-2
2
Задание 4
Задача 1.
Три стрелка стреляют в цель независимо друг от друга. Первый стрелок попадает в
цель с вероятностью 0,6, второй – с вероятностью 0,7, а третий - с вероятностью 0,75.
Найти вероятность хотя бы одного попадания в цель, если каждый стрелок сделает по
одному выстрелу.
Задача 2.
Структура занятых в региональном отделении крупной туристической фирмы имеет вид:
Структура
Женщины
Мужчины
Администрация
25
15
Операционисты
35
25
Если один из служащих выбран случайным образом, то какова вероятность, что он: а)
мужчина-администратор; б) мужчина; в) операционист?
Задача 3.
Имеются
пять
урн
следующего
состава:
2
урны(состава
A1 )
по
2
белых
и
3
черных
шара,
2
урны(состава
А2 )
по
1
белому
и
4
черных
шара,
1
урна
(состава
A3
)—4белых
и
1черный
шар.
Из одной наудачу выбранной урны взят шар. Он оказался белым (событие В). Чему равна после
опыта вероятность (апостериорная вероятность) того, что шар вынут из урны третьего состава?
Задача 4.
В большой рекламной фирме 21% работников получают высокую заработную плату.
Известно также, что 40% работников фирмы - женщины, а 6,4% работников - женщины,
получающие высокую заработную плату. Можно ли утверждать, что на фирме существует
дискриминация женщин в оплате труда.
Задача 5.
Студент пришел на экзамен, изучив только 20 из 25 вопросов. Экзаменатор задал студенту 3
вопроса. Вычислить вероятность того, что студент ответит: а) на все 3 вопроса; б) хотя бы на один
вопрос.
Задача 6.
Вероятность того, что потребитель увидит рекламу определенного лекарственного средства
телевидению равна 0,04. Вероятность того, что потребитель увидит то же средство на рекламном
стенде равна 0,06. Предполагается, что оба события независимы. Чему равна вероятность того, что
потребитель увидит: а) обе рекламы; б) хотя бы одну рекламу.
Задача 7.
Туристическая фирма претендует на 2 заказа от 2 крупных корпораций. Эксперты фирмы
считают, что вероятность получения работы в корпорации А равна 0,45. Эксперты также полагают,
что если фирма получит заказ у корпорации А, то вероятность того, что и корпорация В обратится
к ним равна 0,49. Какова вероятность того, что спортивная фирма получит оба заказа?
Задача 8.
Ожидается прибытие трех судов с фруктами. Статистика показывает, что 1% судов привозят
товар,
не
пригодный
к
употреблению.
Найти
вероятность
того,
что
а)
хотя
бы
два
судна
привезут
качественный
товар;
б) ни одно судно не привезет качественный товар.
Задача 9.
Вероятность того, что клиент банка не вернет заем в период экономического роста равна
0,04, а в период экономического кризиса -0,13. Предположим, что вероятность того, что начнется
период экономического роста равна 0,65. Чему равна вероятность того, что случайно выбранный
клиент банка не вернет полученный кредит?
Задача 10.
Вероятность того, что новое лекарство будет пользоваться спросом на рынке, если конкурент
не выпустит в продажу аналогичный продукт, равна 0,67. Вероятность того, что лекарство будет
пользоваться спросом при наличии на рынке конкурирующего товара, равна 0,42. Вероятность
того, что конкурирующая фирма выпустит аналогичное лекарство равно 0,35. Чему равна
вероятность того, что лекарство будет иметь спрос?
Задача 11
Преподаватель вызвал через старосту на обязательную консультацию трех студентов из
шести отстающих. Староста забыл фамилии студентов и послал наудачу трех отстающих
студентов. Какова вероятность того, что староста послал именно тех студентов, которых назвал
преподаватель?
Задача 12
С конвейера сходит а среднем 85% изделий первого сорта. Сколько изделий необходимо
взять, чтобы с вероятностью 0,997 отклонение доли изделий первого сорта среди отобранных
от 0,85 не превосходило 0,01 (по абсолютной величине)?
Задача 13
Предположим, что вероятность получить выпускнику определенную работу равна 0,4 (Р(А)),
вероятность получить другую работу – 0,5 (Р(В)), вероятность получить предложения на оба места
работы 0,3 (Р(АВ)). Найти вероятность получения для него по крайней мере одного из мест
работы.
Задача14
Из поступивших в магазин телефонов третья часть белого цвета, однако определить цвет
можно только после вскрытия упаковки. Найти вероятность того, что из шести распакованных;
телефонов. а) два аппарата белого цвета; б) хотя бы одни аппарат белого цвета в упаковке
Задача 15
Даны вероятности значений случайной величины X: 2, 4, 8, 10 и их вероятности P: 0,4; 0,2;
0,1; 0,3. Построить ряд распределения, полигон распределения, найти математическое ожидание и
дисперсию случайной величины.
Задача 16
Случайная величина X задана функцией распределения (интегральной функцией)
0
ïðè x  1,


F (x)   (x - 1)/2
ïðè 1  x  3,
 0
ïðè x  3.

Вычислить вероятности попадания случайной величины X в интервалы (1,5; 2,5) и (2,5; 3,5).
Задача 17
Случайная величина X подчинена закону распределения с плотностью
0
ïðè x  0,


f ( x)   a sinx
ïðè 0  x   ,

0
ïðè x   .

Требуется: 1) найти коэффициент a; 2) найти вероятность попадания случайной величины X на
участок (a/2,a); 3) построить график распределения плотности вероятности.
Задача 18
Случайная величина X характеризуется рядом распределения:
xi
0
1
2
3
4
pi
0,2
0,4
0,3
0,08
0,02
Определить математическое ожидание и дисперсию.
Задача 19
Дана функция
0
ïðè x  0,


F ( x)    (4x - x 3 )
ïðè 0  x  2,

0
ïðè x  2.

При каком значении  функция f (x) может быть принята за плотность вероятности
случайной величины X? Определить это значение , найти математическое ожидание и среднее
квадратичное отклонение соответствующей случайной величины X.
Задача 20.
Вычислить дисперсию и среднее квадратическое отклонение для случайной величины с
равномерным распределением.
Задача 21
Случайная величина X распределена по нормальному закону с математическим ожиданием
m=40 и дисперсией D=200. Вычислить вероятность попадания случайной величины в интервал (30,
80).
Задача 22
Случайная величина X распределена по нормальному закону с математическим ожиданием m
= 40 и дисперсией D=200. Вычислить вероятность попадания случайной величины в интервал
(30,80).
Задача 23.
Найти среднее значение случайной величины, заданной распределением
X
13,8
13,9
14
14,1
14,2
nx
4
3
7
6
5
Задача 24.
Найти среднее значение, дисперсию и среднее квадратичное отклонение случайной
величины, заданной распределением
X
9,8
9,9
10
10,1
10,2
nx
1
5
8
4
2
Задача 25.
Дано статистическое распределение:
X
11
12
13
Wx
0,4
0,1
0,3
Найти статистическую функцию распределения и построить ее график.
Вариант
Вариант
Номера задач
(№ в списке)
(№ в списке)
1
1, 22
21
2
2, 23
22
3
3, 24
23
4
4, 25
24
5
5, 21
25
6
6, 19
26
7
7, 18
27
8
8, 29
28
9
9, 23
29
10
10, 22
30
11
11, 23
31
12
12,24
32
14
0,2
Номера задач
12, 24
13, 25
14, 20
15, 19
16, 18
17, 25
18, 21
19, 22
20, 23
21, 24
1, 25
2, 18
13
14
15
16
17
18
19
20
10,22
9,24
8,22
7,20
11,25
12,22
13,24
15,20
33
34
35
36
37
38
39
40
3, 19
2,23
4,20
5,21
17,24
13,20
6,24
3,22
Рекомендуемая литература:
Основная.
1. Баврин, И. И. Высшая математика [Текст]: учебник / И.И. Баврин. - 3-е изд., стер. - М. :
Академия, 2003. - 612 с
2. Баврин, И. И. Высшая математика [Текст]: учебник / И.И.Баврин. - 4-е изд., испр. и доп. М.: Академия, 2004. - 612 с
3. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. - Б.г. Данко П.Е. Ч. 1
[Текст] / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 5-е изд., испр. - М.: Высш. шк., 1999.
- 416 с.
Дополнительная.
1. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. - Б.г. Данко П.Е. Ч. 1
[Текст] / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд. - М. : Мир и образование,
2003. - 304 с.Райхмист Р.Б. Графики функций – М.: Высшая школа, 2001 – 160 с.
2. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. - Б.г. Данко П.Е. Ч. 1
[Текст] / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд. - М. : Мир и образование,
2003. - 304 с.
3. Лутфуллин Ю.Р., Баянова Л.Н. Экономическая теория: вопросы и ответы: учебнометодическое пособие – Уфа: БашИФК, 2008 – 50 с.
Подготовил к.физ-мат.н., ст. препод. Каф ЕНД
Н.Н.Юсупова
Вопросы контрольных работ для студентов 1 курса по специальности 100103 «Социальнокультурный сервис и туризм» обсуждены и приняты на заседании кафедры ЕНД протокол № 3 от
«1» октября 2010 г.
Зав. кафедрой ЕНД
к.б.н., доцент
И.Д. Тупиев