1 - unihub
реклама

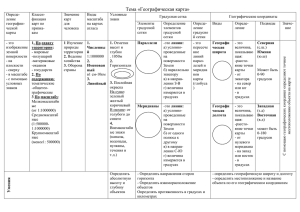
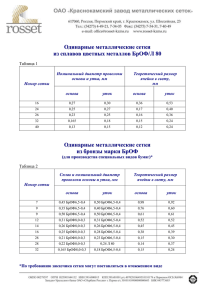
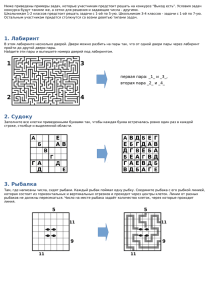
Возможности OpenFOAM для построения расчетных сеток Сергей Стрижак 21.11.2013-22.11.2013 Основные этапы решения задач МСС Различные конечно-объемные элементы в OpenFOAM Метод конечных объемов, I • Метод конечных объемов (FVM) используется для аппроксимации законов сохранения • Вычислительная область разбивается на конечное число непересекающихся контрольных объемов произвольной многогранной формы • Структура данных: – Вершины – Ребра (соединяют вершины) – Грани (замкнутый многоугольник из ребер) – Ячейки (объемы ограниченные гранями) Метод конечных объемов, II • В методе конечных объемов используется три уровня аппроксимации: – Аппроксимация интегралов по поверхности, объему и времени – Интерполяция в точках, отличных от расчетных (центры ячеек) – Численное дифференцирование (аппроксимация градиентов) • Простейшие аппроксимации второго порядка точности (применимые для контрольного объема произвольной формы): – Метод средней точки для интегралов (Midpoint rule), – Линейная интерполяция, – Центральные разности (линейные функции формы). Простые аппроксимации, I • Примеры простых аппроксимаций второго порядка точности, применимых для произвольных многогранных контрольных объемов: Простые аппроксимации, II • Для аппроксимации диффузионного потока необходимо знать производную в направлении перпендикулярном грани ячейки в центре грани... • Некоторые простые апроксимации второго порядка точности, применимые для произвольных многогранных ячеек: Основные утилиты в OpenFOAM для работы с сетками, I • • • • • • • blockMesh – блочный генератор сетки checkMesh -allTopology -allGeometry – проверка качества сетки extrude2DMesh – создание 3D сетки конечной толщины на базе 2D сетки extrudeMesh – выдавливание сетки из существующего патча refineMesh -утилита для измельчения ячеек в нескольких направлений snappyHexMesh – утилита для построения адаптированной сетки с использованием фоновой сетки на базе STL геометрии polyDualMesh – утилита для построения многогранных (polyhedral) сеток Основные утилиты в OpenFOAM для работы с сетками, II • mergeMeshes - объединение двух сеток • mirrorMesh – построение зеркальной сетки относительно выбранной плоскости • moveDynamicMesh – движение сетки и топологическое изменение сетки • moveMesh - решатель для подвижных сеток • moveEngineMesh – решатель для подвижных сеток в камере ДВС • rotateMesh - вращение сетки и полей от направления n1 к направлению n2 • splitMeshRegions - расщепление сетки на несколько областей Основные утилиты в OpenFOAM для работы с сетками, III • attachMesh - подсоединение топологически отсоединенной сетки, использую заранее заданные сеточные настройки • autoPatch - разбиение внешних граней на патчи основанные на заданном угле пользователем • createPatch – утилита для создания патчей вне выбранных граничных граней. Faces come either from existing patches or from a faceSet • setSet - манипуляция a cell/face/point/ set или зоной интерактивно • transformPoints – трансформация узлов сетки в polyMesh директорию согласно translate, rotate and scale опциям • zipUpMesh - Reads in a mesh with hanging vertices and zips up the cells to guarantee that all polyhedral cells of valid shape are closed Сетки из тетраэдров Легко создаются автоматически, но не являются оптимальными: – Только 4 соседа (слишком мало для точной аппроксимации градиентов); - Расположение соседей может быть неблагоприятным... Для решателя необходимы особые критерии, чтобы достичь приемлемой точности на искаженных сетках (distorted meshes)... Неблагоприятное соотношение между числом ячеек и качеством решения... Милован Перич CD-adapco, 2007 Сетки с усеченными ячейками (Trimmed Grids) • Эти сетки преимущественно гексагональные (обычно Декартовы), с некоторым количеством многогранных ячеек в области обрезки... • Эти сетки обычно имеют оптимальные параметры (основную сетку можно растянуть...) Сетки из многогранных ячеек Сетки из многогранных ячеек можно создавать автоматически также просто, как и сетки из тетраэдров – однако эти сетки имеют ряд преимуществ: – Всегда достаточно соседей для вычисления градиентов (обычно 10 – 12) – Пространственное расположение соседей более благоприятно... Почему многогранные ячейки? • Расширение возможностей метода дискретизации и решения уравнений для работы с произвольными многогранными ячейками преследует несколько целей: Устранение ограничений по форме ячеек (делая любую форму ячейки приемлемой); Унификация работы программы в некоторых особых случаях ; Упрощение кода и структуры данных, увеличение модульности программы; Увеличение надежности программы; Упрощение поддержки и расширения программного продукта... Модель аппарата-зонда ‘Сканлайнер’ Модель построена в пакете Solidworks Сетка построена в ICEM CFD. Tetra/prisms Геометрия передана в пакет ICEM CFD Порядок работы: - Создаем геометрию в SolidWorks - Сохраняем файл в формате .stl - Загружаем файл .stl в ICEM CFD 11.0 - Выбираем расчетную область - Выбираем типы контрольных объемов - Строим сетку, проводим контроль - Сохраняем сетку в формате Fluentv6 - Передаем файл в OpenFoam c помощью утилиты “fluent3DMeshToFoam scan.msh” Данные для расчета Расчетная область (-2.0 -0.68 -0.68) - (2.0 0.68 0.68) Расчетная сетка построена на базе тетраэдров Размеры тетраэдров: 1) 100 (inlet) 100 (outlet) 3 (SOL) 2) 80 (inlet) 80 (outlet) 4 (SOL) Общее количество ячеек – 330502 и 451700 Модель URANS с k-w SST моделью турбулентности Tu=1 % , U = 25 м/c (25 0 0 ). Изменение угла атаки (0 4 8 10 градусов) Kin= 0.0937 OMEGAin= 8.22 EPSILONin=0.0693 Dt=0.00025 сек. Time = 0.2 сек. Решатель в OpenFOAM – pisoFoam Утилита checkMesh Create time Create polyMesh for time = 0 Time = 0 Mesh stats points: 62054 faces: 672802 internal faces: 649206 cells: 330502 boundary patches: 3 point zones: 0 face zones: 1 cell zones: 1 Overall number of cells of each type: hexahedra: 0 prisms: 0 wedges: 0 pyramids: 0 tet wedges: 0 tetrahedra: 330502 polyhedra: 0 Checking topology... Boundary definition OK. Point usage OK. Upper triangular ordering OK. Face vertices OK. Number of regions: 1 (OK). Утилита checkMesh Checking patch topology for multiply connected surfaces ... Patch Faces Points Surface topology inlet 412 232 ok (non-closed singly connected) outlet 5736 2894 ok (non-closed singly connected) SOL 17448 8726 ok (closed singly connected) Checking geometry... Overall domain bounding box (-2 -0.679981 -0.679997) (2 0.68 0.68) Mesh (non-empty, non-wedge) directions (1 1 1) Mesh (non-empty) directions (1 1 1) Boundary openness (-2.18538e-19 4.49199e-19 -2.47128e-19) OK. Max cell openness = 1.65939e-16 OK. Max aspect ratio = 11.0456 OK. Minumum face area = 1.26182e-07. Maximum face area = 0.00694694. Face area magnitudes OK. Min volume = 5.42529e-11. Max volume = 0.000201659. Total volume = 5.79848. Cell volumes OK. Mesh non-orthogonality Max: 61.0149 average: 13.3286 Non-orthogonality check OK. Face pyramids OK. Max skewness = 0.913121 OK. Mesh OK. End Пример ‘scanliner’. Многогранные ячейки $ polyDualMesh <angle> <angle> – угол в градусах между гранями ячеек Угол в 40-80 градусов Расчет объема ячейки ? Алгоритм построения ? OpenFOAM-2.2.x / src / conversion / polyDualMesh / polyDualMesh.C Usage: polyDualMesh [OPTIONS] <featureAngle [0-180]> options: -case <dir> specify alternate case directory, default is the cwd -concaveMultiCells split cells on concave boundary edges into multiple cells -constant include the 'constant/' dir in the times list -doNotPreserveFaceZones disable the default behaviour of preserving faceZones by having multiple faces in between cells -latestTime select the latest time -noFunctionObjects do not execute functionObjects -noZero exclude the '0/' dir from the times list, has precedence over the -zeroTime option -overwrite overwrite existing mesh/results files -splitAllFaces have multiple faces in between cells -time <ranges> comma-separated time ranges - eg, ':10,20,40-70,1000:' -srcDoc display source code in browser -doc display application documentation in browser -help print the usage Using: OpenFOAM-2.1.0 (see www.OpenFOAM.org) Build: 2.1.0-bd7367f93311 Применение многогранных ячеек в ядерной энергетике • Моделирование нестационарного растворения бора в корпусе ядерного реактора... • Модель 4-х контурного реактора PWR с перфорированным баком... Automatically generated mesh, resolving geometrical details with STAR-CCM Литература • Jasak H. Error analysis and estimation in the Finite Volume method with application to fluid flows: PhD thesis. Imperial College of Science, Technology and Medicine. L., 1996. 394 p. • Samir Muzaferija, David Gosman. Finite-Volume CFD Procedure and Adaptive Error Control Strategy for Grids of Arbitrary Topology. JOURNAL OF COMPUTATIONAL PHYSICS 138, 766–787 (1997) • Ferziger J.H., Peric M., Computational Methods for Fluid Dynamics. Springer-Verlag, Berlin et al.: Springer, 2002. – 423p. • Peric M. Flow simulation using control volumes of arbitrary polyhedral shape, ERCOFTAC Bulletin, No. 62, September 2004. • Волков К.Н., Емельянов В.Н. Моделирование крупных вихрей в расчетах турбулентных течений. М.: Физматлит, 2008. 368 с.