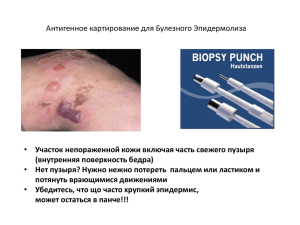
Физика мыльного пузыря

Физика мыльного пузыря
Подготовили:
Жуликов Леонид
Соколов Никита
Черненков Алексей
Под руководством
Ломаченкова И.А.
Постановка задачи
1.
2.
3.
4.
Понять от чего зависит время существования пузыря.
Создать благоприятные для него условия.
Разработка теоретической модели явления.
Разработка экспериментальной методики измерений
Теоретическая модель
τ = t/N
t0=0 , R=R0
v(t) = |ΔR(t)|/τ = δR(t)/τ = cR(t) ,
Где величина c=δ/τ в силу сделанных допущений не зависит от времени.
Зафиксируем значения радиуса пузыря в моменты времени τ, 2τ, 3τ, ... Nτ:
τ: R1=R0-ΔR0 = R0-v0τ= R0(1-cτ)
2τ: R2=R1-ΔR1 = R1 - v1τ = R1(1-cτ) = R0(1-cτ)2
3τ: R3=R2-ΔR2 = R2 - v2τ = R2(1-cτ) = R0(1-cτ)3
...
Nτ: R=R0(1-cτ) N = R0(1-ct/N) N = R0[(1-δ)1/δ]ct
Вывод закономерности
Очевидно, что при 𝑵 → ∞значение величины δ становится
𝒄𝒕
очень малым (𝜹 → 𝟎): 𝜹 = с𝝉 = .Несложная компьютерная
𝑵
программа позволяет найти предел последовательности вида
𝟏 − 𝜹 𝟏/𝜹 при 𝜹 → 𝟎:
𝐥𝐢𝐦 𝟏 − 𝜹
𝜹→𝟎
𝟏/𝜹
=
𝟏
(1)
𝒆
Таким образом, зависимость радиуса пузыря от времени
имеет экспоненциальный характер:
R(t) = R0*e-ct(2)
Экспериментальная установка
Результаты
Тем не менее, полученные опытные данные интересно сравнить с
результатами расчетов по формуле (2). В первом варианте расчетов
величина с, входящая в показатель экспоненты, вычислялась исходя из
значения диаметра пузыря в начальный момент времени t=0 и его значения
спустя время t1 = 30 c: С = 0,0011 с-1
Во втором варианте расчетов С вычислялась, как среднее арифметическое
величин ci , рассчитанных по трем парам значений диаметра пузыря:(d1,d2),
(d3,d4), (d5,d6): C = 0,00067c-1
В третьем варианте аналогичные расчеты величины С проводились в
результате усреднения величин ci , полученных по всем пяти парам значений
диаметра: С = 0,00074с-1
Таблица
График
Таблица
Заключение
1. Существенного ускорения процесса диффузии молекул
воздуха через стенку мыльного пузыря удалось достичь за
счет создания разности концентраций внутри и вне пузыря
2. Изменение радиуса пузыря в процессе диффузионного
«увядания» удовлетворительно описывается
экспоненциальным законом
3. Опытным путем установлено, что «постоянная» С пузыря,
фигурирующая в показателе экспоненциальной функции
оказывается зависящей от времени.
4. . Для количественного изучения процесса диффузии,
например, изменения коэффициента диффузии, необходимо
уметь оценивать толщину пузыря.
Список используемой литературы:
1.
2.
3.
4.
5.
Я.Е.Гегузин. Пузыри. М., Наука, 1985
А. М. ПРОХОРОВ Физическая энциклопедия 1988
И. Ю. Фатиева. Эрудит. Физика
Купер Л. Физика для всех.
Г.С.Ландсберг. Элементарный учебник физики.
Спасибо за внимание!