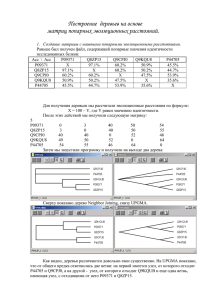
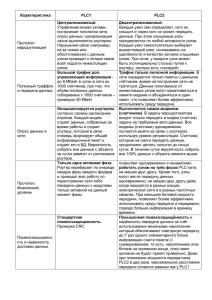
Абрамов К.Г., Монахов Ю.М. Программа для моделирования
реклама

Программа для моделирования распространения нежелательной информации в социальных сетях ModelGraph Абрамов К.Г. 1 Основная задача Программа предназначена для имитационного моделирования распространения спама в социальной сети. 2 Основные характеристики программы 1. Поддержка трех эпидемиологических моделей: SIR, SIM, SIS. 2. Возможность моделирования как на гомогенных, так и на гетерогенных сетях. 3. Поддержка работы с файлами программы Pajek. 4. Наличие функции сохранения результатов моделирования в файл. 5. Наличие функции загрузки результатов моделирования из файла. 6. Возможность анализа перколяционного кластера. 3 Социальная сеть Социальная сеть направлена на построение сообществ в Интернете из людей со схожими интересами и/или деятельностью. Связь осуществляется посредством сервиса внутренней почты или мгновенного обмена сообщениями. 4 Графическое представление моделей Графическое представление SIR модели Графическое представление SIS модели Графическое представление SIM модели S – узел, способный распространять нежелательную информацию; I – узел, распространяемый нежелательную информацию; R, M – узел, распространение нежелательной информации к которому прекращено; 5 Перколяционный кластер Перколяционный кластер представляет собой совокупность связных между собой узлов с высоким кластерным коэффициентом. Перколяционный кластер из иммунизированных узлов. 6 Алгоритм поиска кластера • для всех узлов в сети высчитывается кластерный коэффициент по формуле (1); • задается пороговый коэффициент, значение которого должно находиться между максимальным и минимальным значениями коэффициентов в заданной сети; • берется узел с наибольшим значением кластерного коэффициента и от этого узла через его соседей рекурсивно формируется кластер. Критерий вхождения узла в кластер - значение его кластерного коэффициента должно быть выше порогового. 7 Динамика перколяционного кластера Алгоритм • если в ходе процесса в перколяционном кластере «иммунизируется» узел, то этот узел «выбрасывается» из сети; • пересчитываются кластерные коэффициенты для оставшихся узлов в перколяционном кластере; • если у узла из перколяционного кластера кластерный коэффициент падает ниже порогового, то данный узел «выбрасывается» из сети. 8