Методическая разработка Кицис Л.Г. МОУ КСОШ №1 Всеволожского района
реклама

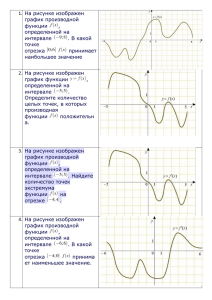
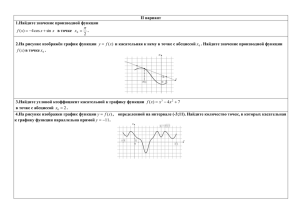
Методическая разработка Кицис Л.Г. МОУ КСОШ №1 Всеволожского района I f (xo) = k = tg 1. На рисунке изображён график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0. Ответ: 0 , 2 5 2. На рисунке изображен график функции у = f(х), определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна. y' >0 => k >0 => y- возрастает Ответ: 4 3. На рисунке изображен график функции у = f(х), определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции у = f(х) отрицательна. y ' <0 => k <0 => y- убывает Ответ: 7 4. На рисунке изображен график функции y=f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней. y = 6 => k =0 => касательная параллельна оси абсцисс Ответ: 4 5. На рисунке изображен график функции y = f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x). 7 1 2 9 10 11 4 Ответ: 4 4 , 6. На рисунке изображен график производной функции у = f (х) , определенной на интервале (- 8;3). В какой точке отрезка [- 3;2] функция принимает наибольшее значение? f '<0 => y = f(x) убывает на данном отрезке => наибольшее значение функция принимает на левом конце Ответ: - 3 , 7. На рисунке изображен график производной у = f (х) функции , определенной на интервале (− 8;4) . В какой точке отрезка [− 7; − 3] функция у = f(х) принимает наименьшее значение? f ' >0 => y = f(x) возрастает на данном отрезке => наименьшее значение функция принимает на левом конце Ответ: - 7 , 8. На рисунке изображен график производной функции у = f (х), определенной на отрезке [−5; 5]. Найдите количество точек максимума функции у = f(х) на отрезке [−4; 3]. у f ‘=0 и меняет знак с “плюса” y = f'(x) -5 1 0 1 5 х Ответ: 1 на“минус” , 9. На рисунке изображен график производной функции у = f (х) , определенной на интервале (− 18;6). Найдите количество точек минимума функции у = f(х) на отрезке [− 13;5]. f ‘ = 0 и меняет знак c “минуса” Ответ: 2 на “плюс” , 10. На рисунке изображен график производной функции у = f (x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции у = f(х) на отрезке [−10; 10]. Ответ: 5 , 11.На рисунке изображен график производной функции у = f (x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции у = f(x). В ответе укажите сумму целых точек, входящих в эти промежутки. Ответ: - 3 12. На рисунке изображен график функции y=f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите f'(8). Ответ: 1 , 2 5 , 13. На рисунке изображен график производной функции у = f (x), определенной на интервале (−11; 3). Найдите промежутки возрастания функции у = f(x). В ответе укажите длину наибольшего из них. Ответ: 6 , 14. На рисунке изображен график производной функции у = f (x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции у = f(x) параллельна прямой y = −2x − 11 или совпадает с ней. Ответ: 5 15. На рисунке изображен график производной функции у = f ,(x), определенной на интервале (−4; 8). Найдите точку экстремума функции у = f(x) на отрезке [0; 6]. у у = f ,(x) 1 0 1 х Ответ: 4 , 14. На рисунке изображен график функции у = f (x), определенной на интервале (−5; 5). Найдите количество точек, в которых производная функции у = f(x) равна 0. Ответ: 3 , 16. На рисунке изображён график производной функции у = f (x), и восемь точек на оси абсцисс: х1, х2, …, х8. В скольких из этих точек функция у = f(x) убывает? у = f ,(x) Ответ: 5 17. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0. Ответ: - 2 18. На рисунке изображен график функции и отмечены точки −2, −1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку. Ответ: - 2