proc glm
реклама

SAS/STAT LECTURE 1
ВВЕДЕНИЕ. ДИСПЕРСИОННЫЙ АНАЛИЗ
Павел Гребенников pgrebennikov@ibs.ru
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
SAS/STAT ОБЗОР КУРСА
•
•
•
•
ANOVA – дисперсионный анализ
LINEAR REGRESSION – линейная регрессия
LOGISTIC REGRESSION – логистическая регрессия
Generalized LM – обобщенные линейные модели
• POISSON REGRESSION & ZERO-INFLATED POISSON
• NEGATIVE BINOMIAL REGRESSION
• GAMMA REGRESSION
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ПОМОЩЬ
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
SAS/STAT ГДЕ ИСКАТЬ ПОМОЩИ….
•
HTTP://SUPPORT.SAS.COM/DOCUMENTATION/ONLINEDOC/STAT/INDEX.HTML
•
HTTP://WWW.MACHINELEARNING.RU
•
HTTP://STANFORD.EDU/
•
HTTPS://WWW.GOOGLE.RU/
•
HTTP://EN.WIKIPEDIA.ORG/WIKI/ANALYSIS_OF_VARIANCE
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ АНАЛИЗ
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ПРИМЕРЫ ЗАДАЧ
АНАЛИЗ
•
Действительно ли учителя в среднем зарабатывают меньше бухгалтеров?
•
Правда ли у людей получающих новое лекарство уровень лимфоцитов больше чем у
людей получающих плацебо?
•
Рыбы живущие в реках около вулканов больше чем рыбы живущие далеко от вулканов?
•
Влияет ли осведомленность потребителей о магазинах сети «Перекресток» (высокая,
средняя, низкая) на предпочтение магазинов именно этой сети?
•
Как уровень рекламы и/или уровень цен (высокий, средний, низкий) одновременно
влияют на объем продаж товаров данной торговой марки?
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ОБЩАЯ ЗАДАЧА
АНАЛИЗ
Есть ли разница между средними характеристики нескольких популяций/выборок/групп?
Predictor
Response
One-Way
ANOVA
Categorical
Continuous
Или по-другому:
«Помогает» ли информация о принадлежности к гр пе предсказать значение
исследуемой характеристики?
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ВВЕДЕНИЕ ПЕРЕМЕННЫЕ
• Variable type
• Continuous: температура, зарплата, возраст, …
• Categorical (= class): образование, пол, тип тарифного плана, регион, …
• Categorical level of measurement
• Nominal – порядок не определен.
• Ordinal – порядок определен [ => числовые].
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ANOVA И ДРУГИЕ МОДЕЛИ
АНАЛИЗ
Type of
Predictors
Categorical
Continuous
Continuous and
Categorical
Continuous
Analysis of
Variance
(ANOVA)
Ordinary Least
Squares (OLS)
Regression
Analysis of
Covariance
(ANCOVA)
Categorical
Contingency
Table Analysis or
Logistic
Regression
Logistic
Regression
Logistic Regression
Type of
Response
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ЧЕСНОК
АНАЛИЗ
4 Fertilizers
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
32 Beds
ДИСПЕРСИОННЫЙ
GARLIC DATASET
АНАЛИЗ
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ГИПОТЕЗА ДИСПЕРСИОННОГО АНАЛИЗА
АНАЛИЗ
H0: F1=F2=F3=F4
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
H1: F1 ≠ F2 or F1 ≠ F3
or F1 ≠ F4 or F2 ≠ F3
or F2 ≠ F4 or F3 ≠ F4
ДИСПЕРСИОННЫЙ
ОСНОВНАЯ ЛОГИКА ДИСПЕРСИОННОГО АНАЛИЗА
АНАЛИЗ
Variability
Variability
between Groups within Groups
Суммы
квадратов
Total Variability
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
SST
=
SSM
+ SSE
ДИСПЕРСИОННЫЙ
СУММЫ КВАДРАТОВ: ПРИМЕР
АНАЛИЗ
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
СУММЫ КВАДРАТОВ: ПРИМЕР [TOTAL SUM OF SQUARES]
АНАЛИЗ
SST =
(7-6)2
(3-6)2
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
(7-6)2 +
(8-6)2 +
(9-6)2 +
(3-6)2 +
(4-6)2 +
(5-6)2 +
= 28
ДИСПЕРСИОННЫЙ
СУММЫ КВАДРАТОВ: ПРИМЕР [ERROR SUM OF SQUARES]
АНАЛИЗ
SSE =
YB 8
(7-8)2
YA 4
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
(5-4)2
(7-8)2 +
(8-8)2 +
(9-8)2 +
(3-4)2 +
(4-4)2 +
(5-4)2
=4
ДИСПЕРСИОННЫЙ
СУММЫ КВАДРАТОВ: ПРИМЕР [MODEL SUM OF SQUARES]
АНАЛИЗ
YB 8
(8-6)2
YA 4
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
(4-6)2
SSM = 3*(4-6)2 +
3*(8-6)2 = 24
ДИСПЕРСИОННЫЙ
F STATISTIC AND CRITICAL VALUES AT =0.05
АНАЛИЗ
𝑭 .,. =
𝑀𝑆𝑀
𝑀𝑆𝐸
=
𝑆𝑆𝑀
𝑀𝑜𝑑𝑒𝑙𝐷𝐹
𝑆𝑆𝐸
𝐸𝑟𝑟𝑜𝑟𝐷𝐹
ModelDF = число групп -1
ErrorDF=Nobs -1 - (ModelDF)
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
F STATISTIC SIMPLE “LOGIC”
АНАЛИЗ
YB 8
YA 4
F >> 1
F~1
R2= SSM / SST
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
СПЕЦИФИКАЦИЯ МОДЕЛИ
АНАЛИЗ
BulbWt =
Yik
Base
+ Fertilizer + Unaccounted
Level
for Variation
= + i + ik
proc glm data=sasuser.MGGarlic;
class Fertilizer;
model BulbWt=Fertilizer;
title 'Testing for Equality of Means with PROC GLM';
run; quit;
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ПРЕДПОЛОЖЕНИЯ
АНАЛИЗ
• Наблюдения независимы
• Good data collection designs help ensure the independence assumption
• Ошибка нормально распределена
• Diagnostic plots from PROC GLM
• Во всех группах одинаковая дисперсия
• PROC GLM produces a test of equal variances with the HOVTEST option in
the MEANS statement.
H0 for this hypothesis test is that the variances are equal for all
populations
if NO then ask for: MEANS <GROUP-VAR> / HOVTEST WELCH;
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ПРИМЕР
АНАЛИЗ
proc glm data=sasuser.MGGarlic plots(only)=diagnostics;
class Fertilizer;
model BulbWt=Fertilizer;
means Fertilizer / hovtest WELCH;
title 'Testing for Equality of Means with PROC GLM';
run;
quit;
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ПРИМЕР – РЕЗУЛЬТАТЫ
АНАЛИЗ
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ПРИМЕР – РЕЗУЛЬТАТЫ
АНАЛИЗ
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ПРИМЕР – РЕЗУЛЬТАТЫ
АНАЛИЗ
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ПРИМЕР – РЕЗУЛЬТАТЫ
АНАЛИЗ
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
OBSERVATIONAL OR RETROSPECTIVE STUDIES
АНАЛИЗ
•
Часто мы смотрим на то, что уже случилось (retrospective),
вместо планирования будущего результата (prospective).
•
У нас нет возможности контролировать факторы, влияющие
на исследуемый параметр.
Планирование экспериментов?
КОНТРОЛИРУЕМЫЙ ЭКСПЕРИМЕНТ:
RANDOMIZE BLOCK DESIGN
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ФАКТОРЫ-ПОМЕХИ
АНАЛИЗ
?
Bulb
Weight
?
Fertilizer
?
SST
SSM
SSE
F( , )=MSM / MSE
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ДОПОЛНИТЕЛЬНЫЕ ПРЕДПОЛОЖЕНИЯ
АНАЛИЗ
• Внутри каждого блока группы присваиваются каждому
объекту исследования случайно.
• В нашем примере: на грядках внутри каждого сектора
используются случайное удобрение
• Влияние группы должно быть постоянным для всех
блоков.
• Т.е. между переменной Sector и Fertilizer не должно быть стат.
значимого пересечения (interaction).
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
БЛОКИ
АНАЛИЗ
4 Fertilizers
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
32 Beds
8 Sectors
ДИСПЕРСИОННЫЙ
ПРИМЕР
АНАЛИЗ
proc glm data=sasuser.MGGarlic_Block plots(only)=diagnostics;
class Fertilizer Sector;
model BulbWt=Fertilizer Sector;
title 'ANOVA for Randomized Block Design';
run;
quit;
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ПРИМЕР - РЕЗУЛЬТАТЫ
АНАЛИЗ
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
СРЕДНИЕ В ГРУППАХ РАЗЛИЧНЫ, ЧТО ТЕПЕРЬ?
АНАЛИЗ
Tukey
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
Dunnett
ДИСПЕРСИОННЫЙ
МЕТОДЫ МНОЖЕСТВЕННОГО СРАВНЕНИЯ
АНАЛИЗ
Задача1. Бросаем монету. Вероятность выпадения «орла» = 0,5.
Если при первом бросании выпал «орел», то какова
вероятность выпадения «орла» при втором бросании?
0,5
Задача1. Бросаем монету. Вероятность выпадения «орла» = 0,5.
Какова вероятность выпадения хотя бы одного «орла» при двух
бросаниях?
0,75
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
МЕТОДЫ МНОЖЕСТВЕННОГО СРАВНЕНИЯ
АНАЛИЗ
Comparisonwise
Error Rate (=0.05)
Number of
Comparisons
Experimentwise
Error Rate (=0.05)
.05
1
.05
.05
3
.14
.05
6
.26
.05
10
.40
EER 1 – (1 - )nc
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ПРИМЕР
АНАЛИЗ
proc glm data=sasuser.MGGarlic_Block
plots(only)=(controlplot diffplot(center));
class Fertilizer Sector;
model BulbWt=Fertilizer Sector;
lsmeans Fertilizer / pdiff=all adjust=tukey;
lsmeans Fertilizer / pdiff=control('4') adjust=dunnett;
lsmeans Fertilizer / pdiff=all adjust=t;
title 'Garlic Data: Multiple Comparisons';
run;
quit;
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ ДВУХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ С
АНАЛИЗ ПЕРЕСЕЧЕНИЯМИ
Response
Categorical
Predictor
One-Way
ANOVA
1 Predictor
n-Way
ANOVA
Continuous
More than
1 Predictor
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
DRUG EXAMPLE
АНАЛИЗ
The purpose of the study is to look at the effect of a new
prescription drug on blood pressure.
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
INTERACTIONS
АНАЛИЗ
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
NONSIGNIFICANT INTERACTIONS
АНАЛИЗ
Analyze the main effects with the interaction in the model.
Yijk i j ij ijk
…or…
Delete the interaction from the model, and then analyze the
main effects.
Yijk i j ijk
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
NONSIGNIFICANT INTERACTIONS: GUIDES
АНАЛИЗ
Guidelines when to delete the interaction from the model:
• < 5 DF for the error
• F-value for the interaction term < 2
Note: when you analyze data from an observational study, it is more
common to delete non-significant interaction and then analyze the
main effects.
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ПРИМЕР: TWO-WAY ANOVA WITH INTERACTIONS
АНАЛИЗ
ods graphics on;
proc glm data=sasuser.drug order=internal;
class DrugDose Disease;
model Bloodp=DrugDose Disease DrugDose*Disease;
lsmeans DrugDose*Disease / slice=Disease;
title 'Analyze the Effects of DrugDose';
title2 'at Each Level of Disease';
format DrugDose dosefmt.;
run;
quit;
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ПРИМЕР: TWO-WAY ANOVA WITH INTERACTIONS
АНАЛИЗ
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ПРИМЕР: TWO-WAY ANOVA WITH INTERACTIONS
АНАЛИЗ
1 – Placebo
2 – 50 mg
3 – 100 mg
4 – 200 mg
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
ДИСПЕРСИОННЫЙ
ПРИМЕР: TWO-WAY ANOVA WITH INTERACTIONS
АНАЛИЗ
1 – Placebo
2 – 50 mg
3 – 100 mg
4 – 200 mg
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .
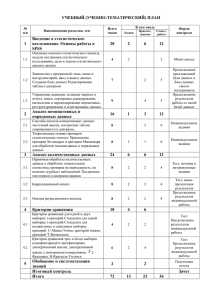
HOME WORK
C op yr i g h t © 2 0 1 3 , S A S I n s t i t u t e I n c . A l l r i g h t s r es er v e d .