Генерация простых чисел Миронович Светлана Юрьевна

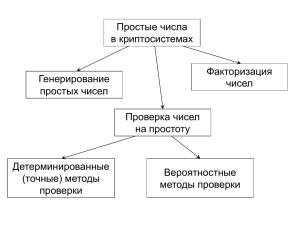
Генерация простых чисел
Миронович Светлана Юрьевна
Генерация простых
Есть два подхода.
A: проверка простоты
1. Выбираем случайно n {2^{k-1},…,2^k}
2. M(n)-ПВМТ, допускает одностороннюю
ошибку. Говорит о том, является ли n
вероятно простым
3. Если M(n)=1, то возвращаем n
B: построение простых
1. n – натуральное специального вида (этот вид
известен противнику)
2. M – специальная МТ распознавания простоты
3. Если M(n)=1, то возвратить n
Распределение простых
Алгоритм проверки простоты:
Вход: kN (битовая длина)
Выход: n – k-битное вероятно простое
Шаги: 1. случайно выбираем неч.k-битное число
n
2. Для i=1,…,d:
1)Если M(n)=0, то вернуться в ш.1
3. Возвратить n
Если (x) – количество простых чисел ≤ x, то
(x) = x/ln(x), x →∞
Тест Ферма
n – псевдопростое по основанию а, если
a^{n-1} = 1 mod n.
Алгоритм теста Ферма:
• Вход: nN
• Выход: 1, если n вероятно простое, иначе 0
• Шаги:
1. a  {1,2,…,n-1}
2. Если (a,n) ≠ 1, то возвратить 0
3. Если a^{n-1} ≠ 1 mod n, то возвратить 0
4. Возвратить 1
Тест Рабина-Миллера
n=2^s * r + 1, r неч. – сильно псевдопростое по основанию а,
если: a^r = 1 mod n и a^{r*2^i} = -1mod n
Алгоритм теста Миллера-Рабина:
• Вход: nN, n=r*2^s + 1, r неч.
• Выход: 1, если n вероятно простое, иначе 0
• Шаги:
1. a  {1,2,…,n-1}
2. Если (a,n) > 1, то возвратить 0
3. u a^r mod n
4. Если u=1 mod n, то возвратить 1
5. Для I = 0,1,…,s-1:
1)u=-1 mod n, то возвратить 1
2)u  u^2 mod n
6. Возвратить 0
Построение простых
Теорема Диемитко: n=qR+1, q-простое, R-четное, R <
4(q+1). Если 2^{qR} = 1 mod n и 2^R ≠ 1 mod n, то n –
простое.
Схема генерации:
L_0 – битовая длина окончательного простого числа, L_1
= (L_0+1)/2,…, L_d = (L_(d-1)+1)/2
L_d мало (≤32,16). Начинаем справа, берем простое p_d
битовой длины L_d. Двигаемся влево, определяем
простые числа для i:d-1,…,0: p_i  p_{i+1}*R_i + 1, R_i
– выбрано случайно так, чтобы удовлетворять
теореме Диемитко
P_0 – искомое простое заданной длины