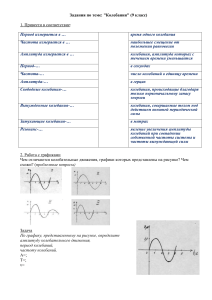
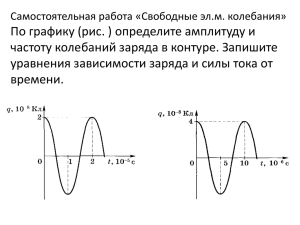
 a x  

x  A sin(t  0 )
 x   A cos(t  0 )
ax   A sin(t  0 )
2
ax   x
2
Проекция ускорения колеблющегося тела на ось ОХ
прямо пропорциональна модулю смещения, а направление
ускорения противоположно направлению смещения.
Алгоритм вывода формулы для периода малых колебаний:
1. Определить какая сила будет возвращающейся.
2. Записать II закон Ньютона в проекциях на ось ОХ.
3. Привести уравнение к виду: ax  kx
4. Вывести формулу для расчета угловой частоты:   k
5. Вывести формулу для периода малых колебаний:
T
2

Покажем на примере пружинного маятника, что для вывода формулы
периода колебании, достаточно учитывать только возвращающую силу.
Х
Тогда согласно второму закону Ньютона, получим:
F2  mg  ma
Î X : k ( x1  x)  mg  ma
F1  mg  ma
Î X : kx1  mg  0  kx1  mg
0
kx1  kx  mg  ma
kx
kx   ma  a  
m
1
2
a

k
m
 T  2
m
k
Ускорение тела, колеблющегося на
пружине, не зависит от силы тяжести,
действующей на это тело. Сила тяжести
только приводит к изменению положения
равновесия. Эту зависимость можно
получить, если изначально учитывать только
возвращающую силу, в данном случаеF   kx.
2
Колеблющиеся тела, которые встречаются в задачах
для определения периода малых колебаний.
Ареометр
Колебания жидкости,
которую вывели из
положения равновесия
Колебания поршня
Колебания бусинки,
расположенной
между двумя зарядами
Колебания тела, на границе Колебания тела, между
закрепленными пружинами
раздела жидкостей
С1 . Ареометр, погруженный в жидкость, совершает вертикальные гармонические колебания
с малой амплитудой. Найдите период этих колебаний. Масса ареометра равна 40 г,
радиус его трубки 2 мм, плотность жидкости 0,8 г/см3. Сопротивлением жидкости можно
пренебречь.
Х
Дано:
m = 40 г
R = 2 мм
  0,8 ã / ñì
a
3
T-?
О

 gS
На ареометр, смещенный от
положения равновесия на расстояние x,
действует избыточная архимедова сила,
которую называют возвращающей .
OX : FA  ma
 g V  ma
  gSx  ma
 gS

xa
a   2 x
m
2
m
m
2 m
T 
 2
 2

2
m

 gS
 g R
R g
T  4c.
Ответ: 4 с.