Поток вектора магнитной индукции
реклама
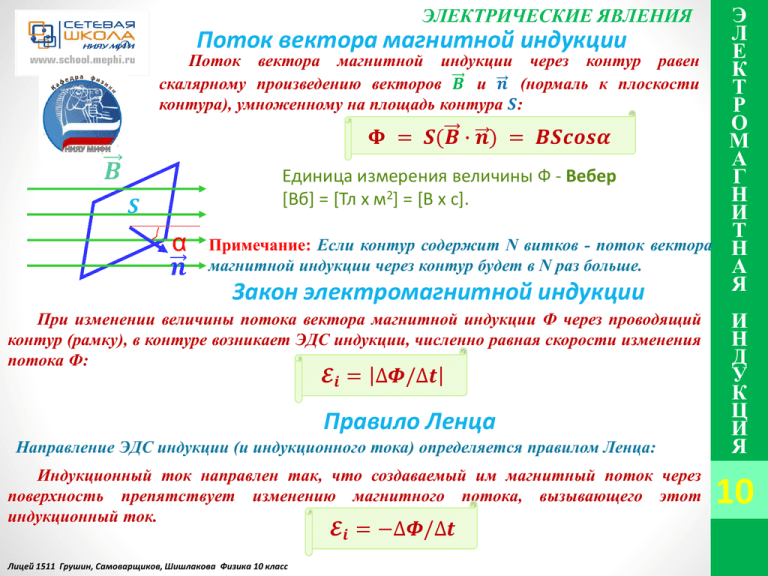
ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ Поток вектора магнитной индукции Поток вектора магнитной индукции через контур равен скалярному произведению векторов 𝑩 и 𝒏 (нормаль к плоскости контура), умноженному на площадь контура 𝑺: 𝚽 = 𝑺(𝑩 ∙ 𝒏) = 𝑩𝑺𝒄𝒐𝒔𝜶 𝑩 Единица измерения величины Ф - Вебер [Вб] = [Тл х м2] = [В х с]. 𝑺 α 𝒏 Примечание: Если контур содержит N витков - поток вектора магнитной индукции через контур будет в N раз больше. Закон электромагнитной индукции При изменении величины потока вектора магнитной индукции Ф через проводящий контур (рамку), в контуре возникает ЭДС индукции, численно равная скорости изменения потока Ф: 𝓔𝒊 = ∆𝜱/∆𝒕 Правило Ленца Направление ЭДС индукции (и индукционного тока) определяется правилом Ленца: Индукционный ток направлен так, что создаваемый им магнитный поток через поверхность препятствует изменению магнитного потока, вызывающего этот индукционный ток. 𝓔𝒊 = −∆𝜱/∆𝒕 Лицей 1511 Грушин, Самоварщиков, Шишлакова Физика 10 класс Э Л Е К Т Р О М А Г Н И Т Н А Я И Н Д У К Ц И Я 10 РЕШЕНИЕ ЗАДАЧ L1=5 ∙ 10−3 Гн L2=3 ∙ 10−3 Гн ℰ=0,5 В r=10 Ом 𝐼0=30 ∙ 10−3 А 𝐼1= ? 𝐼2= ? ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ 24.20. Две катушки, индуктивности которых 𝐿1 = 5мГн и 𝐿2 = 3 мГн, подключены параллельно через ключи К1 и К2 к источнику с ЭДС ε=0,5В и внутренним сопротивлением 𝑟 = 10 Ом . В начальный момент времени оба ключа разомкнуты. После того, как ключ К1 замкнули и ток через катушку L1 достиг некоторого значения 𝐼0 = 30 мА, замыкают ключ К2. Определить установившиеся токи через катушки L1 и L2 после замыкания ключа К2. Сопротивлениями катушек пренебречь. 2. Изобразим схему: 1. Запишем краткое условие: После замыкания ключа К1 ток через L1 будет нарастать. К1 К2 При достижении током величины𝐼0 , в соответствии с условием, замыкается ключ К2 𝓔 L1 L2 При изменении тока в катушке r ∆𝑰 возникает ЭДС самоиндукции, 𝓔𝒊 = −𝑳 значение которой ∆𝒕 Для идеальной катушки индуктивности (не имеющей сопротивления) 𝓔𝒊 равна по модулю и противоположна по знаку напряжению на концах катушки: 𝓔𝒊 = −𝓔𝒊 = 𝑼 После замыкания ключа К2 напряжение на концах катушек L1 и L2 как параллельных ветвях будет одинаково: ∆𝑰𝟏 ∆𝑰𝟐 ∆𝑳𝟏 𝑰𝟏 ∆𝑳𝟐 𝑰𝟐 ∆(𝑳𝟏 𝑰𝟏 − 𝑳𝟐 𝑰𝟐 ) 𝑳𝟏 = 𝑳𝟐 → = → =𝟎→ ∆𝒕 ∆𝒕 ∆𝒕 ∆𝒕 ∆𝒕 В момент замыкания ключа К2 : 𝑰𝟏 = 𝑰 𝟎 , а 𝑰𝟐 = 𝟎 → 𝑳𝟏 𝑰𝟏 − 𝑳𝟐 𝑰𝟐 = 𝒄𝒐𝒏𝒔𝒕 ∗ → 𝑳𝟏 𝑰𝟎 − 𝟎 = 𝒄𝒐𝒏𝒔𝒕 ∗∗ → 𝑳𝟏 𝑰𝟏 − 𝑳𝟐 𝑰𝟐 = 𝑳𝟏 𝑰𝟎 → 𝑳𝟐 𝑰𝟐 = 𝑳𝟏 (𝑰𝟏 − 𝑰𝟎 ) → 𝑳𝟏 (𝑰𝟏 − 𝑰𝟎 ) 𝑰𝟐 = 𝑳𝟐 Продолжение следует Лицей 1511 Грушин, Самоварщиков, Шишлакова Физика 10 класс Э Л Е К Т Р О М А Г Н И Т Н А Я И Н Д У К Ц И Я 10 РЕШЕНИЕ ЗАДАЧ ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ Продолжение 24.20. Две катушки, индуктивности которых 𝐿1 = 5мГн и 𝐿2 = 3 мГн, подключены параллельно через ключи К1 и К2 к источнику с ЭДС 𝜀 =0,5 В и внутренним сопротивлением 𝑟 = 10 𝑂м. В начальный момент времени оба ключа разомкнуты. После того, как ключ К1 замкнули и ток через катушку L1 достиг некоторого значения 𝐼0 = 30 мА, замыкают ключ К2. Определить установившиеся токи через катушки L1 и L2 после замыкания ключа К2. Сопротивлениями катушек пренебречь. L1=5 ∙ 10−3 Гн L2=3 ∙ 10−3 Гн К1 ℰ=0,5 В r=10 Ом 𝓔 𝐼0=30 ∙ 10−3 А L1 r 𝐼1= ? 𝐼2= ? 𝑰𝟏 К2 𝑰𝟐 𝑰 L2 3. Изобразим схему (ключи замкнуты): Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. 𝓔 Ток через источник питания: 𝑰 = = 𝑰𝟏 + 𝑰𝟐 → r 𝓔 𝑰𝟏 𝑳𝟐 + 𝑳𝟏 𝑰𝟏 − 𝑳𝟏 𝑰𝟎 𝓔 𝑳𝟏 (𝑰𝟏 − 𝑰𝟎 ) 𝑳 → 𝟐 r + 𝑳𝟏 𝑰𝟎 = 𝑰𝟏 (𝑳𝟏 +𝑳𝟐 ) → → = 𝑰𝟏 + = 𝑳𝟐 r 𝑳𝟐 𝓔 𝑳𝟐 + 𝑳𝟏 𝑰𝟎 𝑳𝟏 𝑰𝟏 − 𝑳𝟏 𝑰𝟎 3 ∙ 10−3 ∙ 0,05 + 5 ∙ 10−3 ∙ 30 ∙ 10−3 30 ∙ 10−5 r 𝑰 = : 𝑰𝟏 = = = = 37,5 мА 𝟐 𝑳𝟐 5 ∙ 10−3 + 3 ∙ 10−3 8 ∙ 10−3 𝑳𝟏 + 𝑳𝟐 𝓔 𝓔 𝑳𝟐 + 𝑳𝟏 𝑰𝟎 𝟐 𝟐 r 𝑰𝟐 𝑳𝟐 = 𝑳𝟏 −𝑳𝟏 𝑰𝟎 → 𝑰𝟐 𝑳𝟐 𝑳𝟏 + 𝑳𝟐 = 𝑳𝟏 𝑳𝟐 + 𝑳𝟏 𝑰𝟎 − 𝑳𝟏 𝑰𝟎 −𝑳𝟏 𝑳𝟐 𝑰𝟎 → r 𝑳𝟏 + 𝑳𝟐 𝓔 𝑳𝟏 − 𝑳𝟏 𝑰𝟎 5 ∙ 10−3 ∙ 0,05 − 5 ∙ 10−3 ∙ 30 ∙ 10−3 30 ∙ 10−5 r = = 12,5 мА = сократим → 𝑰𝟐 = 𝑳 + 𝑳 −3 + 3 ∙ 10−3 −3 5 ∙ 10 8 ∙ 10 𝟏 𝟐 Ответ: 𝑰𝟏 = 37,5 мА 𝑰𝟐 = 12,5 мА Лицей 1511 Грушин, Самоварщиков, Шишлакова Физика 10 класс Э Л Е К Т Р О М А Г Н И Т Н А Я И Н Д У К Ц И Я 10







