Мультимедийная ование железных дорог
реклама

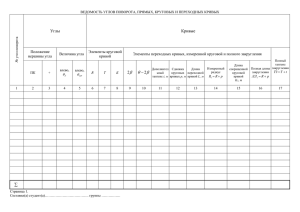
Транспортно – дорожный институт Кафедра «промышленный транспорт» Мультимедийная презентация Изыскания и проектирование железных дорог По дисциплине «Изыскания и проектирование железных дорог» для студентов специальности 5В090100 «Организация перевозок, движения и эксплуатация транспорта» Автор: доцент кафедры ПТ АКАШЕВ АРСЕН ЗАКИРОВИЧ План лекции: 1. Трасса, план и профиль. Элементы плана; 2. Прямые и круговые кривые; 3. Переходные кривые; 4. Смежные кривые; 5. Проектирование плана и его показатели. 1. Трасса, план и профиль. Элементы плана Пространственная линия, состоящая из отрезков прямых, дуг окружностей и спиралей, сопряженных между собой, называется трассой (продольной осью) железной дороги. Трасса проектируется в двух проекциях – в профиле и плане. Проекция трассы на горизонтальную плоскость называется планом; проекция развернутой в плане трассы на вертикальную плоскость – профилем. Элементы плана: прямые, круговые кривые, переходные кривые [1]. 2. Прямые и круговые кривые Прямые. Прямую характеризуют два параметра: длина L и направление, определяемое дирекционным углом β (угол образованный между северным направлением меридиана и направлением прямой). Длина прямой измеряется между концами переходных или круговых кривых. Целесообразность длинных прямых очевидна – обеспечивается кратчайшее расстояние, а следовательно, минимальный пробег подвижного состава и эксплуатационные расходы; конструкции и устройства дороги менее сложные, чем в кривых, что упрощает содержание пути. Конструктивные параметры колеи железнодорожного пути и соответствующие технологические зазоры позволяют осуществлять движение поездов с максимально возможной скоростью. Однако в сложных топографических условиях обход препятствий вынуждает отклоняться от кратчайшего направления. На обходах препятствий приходится «ломать» прямые и устраивать между ними круговые кривые, что в итоге приводит к ограничению скоростей движения поездов. Участок перехода прямой в круговую кривую Круговые кривые. Для плавного сопряжения соседних прямолинейных участков пути устраиваются круговые кривые Кривые разбиваются на местности по параметрам: α – угол поворота; R – радиус; К – длина кривой; Т – тангенс; Б – биссектриса; Д – домер; ВУ – вершина угла поворота. Рисунок 1 - Круговая кривая Основные параметры кривой – угол поворота α и радиус R – назначаются при проектировании плана исходя из целесообразности и экономичности плана, диктуемыми топографическими формами рельефа и плановой ситуацией. Параметры α и R могут изменяться в определенных диапазонах. Минимальный угол поворота αmin ограничивается в зависимости от условий, а максимальный – теоретически не ограничивается. Так, при спиральном развитии линии угол α может быть больше 3600. От радиуса в значительной степени зависит положение дороги в пределах кривой. Минимальный радиус определяется комфортабельностью движения пассажиров. Остальные параметры измеряются в километрах и определяются по формулам: Тангенс кривой: T R * tg 2 (1) Длина кривой: K * R * 180 0 (2) Биссектрисса кривой: Домер: T Б sin 2 R * Д 2 * R * tg 0 2 360 (3) (4) Рассмотрим движение вагона по круговой кривой. На вагон массой m (т), движущийся по кривой радиусом R (м) со скоростью V0 (км/ч), действует центробежная сила F1 (Н), направленная от центра кривой (рис. 2а). Вписывание грузового поезда в кривую (без возвышения наружного рельса) F1 mv02 / R (5) Центробежная сила F1 пропорциональна квадрату скорости и при больших значениях V0 может опрокинуть вагон. Чтобы этого не произошло, наружный рельс в кривой располагают выше внутреннего на величину h – устраивают возвышение наружного рельса, в результате чего возникает сила F2, направленная к центру кривой, т.е. в сторону, противоположную F1 (рис. 2, б). Сила F2 возникает при разложении веса вагона qбр по правилу параллелограмма на две составляющие, она равна F2 = qбрtgα. Вписывание грузового поезда в кривую (с возвышением наружного рельса) а – в плане б – в профиле Рисунок 2 - Движение вагона в кривой Вес вагона qбр равен произведению ее массы m на ускорение силы тяжести g, поэтому F2 gmtg (6) Из треугольника abc (см. рис. 2, б) sinα = h /s, где s – ширина колеи между осями головок рельсов. Угол α мал, поэтому можно принять . Sin tg h / s Произведя замену в формуле 6, получим F2 mgh / s (7) При условии F1 = F2 , то из формул 5 и 6 следует, что mv02 / R mgh / s Или v / R gh / s 2 0 (8) (9) Из формулы 9 можно получить зависимость R от скорости V0 2 0 v S R gh (10) При F1 > F2 будет действовать неуравновешенная центробежная сила ∆F= F1-F2 2 или mv mgh (11) ∆F= R S Если все слагаемые разделить на массу , m то получим: F v gh m R S 2 (12) Отношение неуравновешенной центробежной силы к массе - выражает непогашенное ускорение aнп, и равно: a нп F m (13) Допустимые значения анп = 0,7 м/с2, меньшие значения обеспечивают комфортабельность ощущений пассажиров и сохранность транспортируемого груза. 3. Переходные кривые Переходные кривые. При входе в кривую в точке сопряжения круговой кривой с прямой каждый вагон испытывает боковой удар, происхождение которого связано с внезапным появлением центробежной силы [1]. Центробежная сила обратно пропорциональна радиусу кривизны ρ железнодорожного пути: F1 mv / ρ 2 0 (14) На прямой радиус кривизны – бесконечная величина, поэтому F1=0; на кривой ρ = R, поэтому F – конечная величина, определяемая по формуле 5. Сила F1 приводит к износу пути и подвижного состава, а также к нарушению плавности движения. Для предотвращения этого между круговой кривой и прямой вставляется переходная кривая – радиоидальная спираль длиной l0 с переменным радиусом кривизны, обратно пропорциональным длине S p Rl / s (15) Следовательно, в точке НПК - начало переходной кривой, радиус кривизны ρ=∞ (совпадает с радиусом кривизны прямой), в точке КПК - конец переходной кривой, радиус кривизны ρ= R (совпадает с радиусом кривизны круговой кривой). Между точками НПК и КПК радиус кривизны изменяется непрерывно – принимая значения от 0 до величины R. Для плавного движения поезда и предотвращения заклинивания колесной пары необходимо создать уширение колеи с обеспечением допустимых зазоров. В пределах переходной кривой обеспечивается плавный отвод возвышения наружного рельса и уширение колеи в кривых. Возвышение наружного рельса отводится по наклонной линии. Длина переходной кривой l0 (м) равна длине отвода возвышения, которая представляет собой отношения возвышения h(м) к уклону отвода возвышения i (‰). Зазор между гребнем колеса и боковой гранью внутреннего рельса L=h/i . (16) Уклон отвода возвышения i = h/L. (17) Если поезд движется с максимальной скоростью Vmax, то одна вагонная ось его пройдет путь L за время t= L/ Vmax. Откуда L = Vmax*t, тогда i = h/ Vmax*t (18) Отношение h/t представляет собой скорость Vпк подъема колеса по отводу возвышения: Vпк= h/t. Поэтому уклон отвода возвышения i = Vпк/Vmax. Скорость Vпк ограничивается, так как при большой скорости воздействие колеса на рельс на участке отвода возвышения близко к ударному. В средних условиях Vпк =28 мм/с = 1/10 км/ч. Поэтому i =1/10Vmax (19) При Vmax= 100 км/ч i=1/1000=1‰. СНиП поэтому разрешает принимать i более 1‰ только в трудных условиях. Возвышение наружного рельса h sv / gR 12,5 v / R 2 cp 2 cp (20) В эту формулу вводится коэффициент k, учитывающий смещение центра тяжести экипажа в наружную сторону (обычно k =1,2), а скорость принимается средней для всех поездов – так называемая средняя квадратичная скорость υср . С учетом всего этого h k12,5v / R 2 ср (21) Длина переходной кривой: L k12,5v 10vmax / R 2 ср (22) Длины переходных кривых L для среднесетевых условий принимаются по таблице СНиП в зависимости от категории линии, радиуса круговой кривой и зоны скоростей движения поездов. Зоны скоростей характеризует очертание профиля (скорости поездов). К I зоне относятся участки вогнутого очертания и примыкающие к ним спуски, а также участки, на которых скорости поездов максимальны или близки к ним; ко II – участки, проходимые поездами со средней скоростью; к III - участки выпуклого (горбообразного) очертания и примыкающие к ним подъемы, на которых скорости поездов равны расчетно-минимальной или близки к ней. Для устройства переходной кривой центр О круговой кривой радиуса R смещают по биссектрисе в положение О´. Суммарная длина кривой Kc (м) равна сумме длин круговой K и переходной Ɩ0 : Kc = K + Ɩ0 (23) То обстоятельство, что переходная кривая устраивается частично за счет укорочения круговой кривой, приводит к необходимости в отдельных случаях проверять достаточность длины круговой кривой между концами переходной кривой. Минимальная длина участка круговой кривой Kmin между переходными должна быть не менее длины двух пассажирских вагонов, т.е. Kmin = 50 м. Таким образом, K > Kmin + Ɩ0 , или R / 180 K min l0 (24) Если это условие не выполняется, то надо увеличить радиус R или угол поворота α либо уменьшить длину переходной кривой. Минимальный угол поворота min 180K min l0 / R (25) 4. Смежные кривые Смежные кривые. Смежными называются кривые, разделенные прямой вставкой d. Они могут быть направлены в одну сторону – однонаправленные и разнонаправленные. Задача проектирования смежных кривых – установить минимальную длину прямой вставки. Измеряется длина прямой вставки между точками начал переходных кривых [1]. В процессе движения вагона в кривой на него действует неуравновешенная сила ∆F1, под влиянием которой возникают поперечные колебания кузова. Рисунок 3 - Смежные кривые, направленные в одну (а) и в разные (б) стороны При входе в следующую кривую под действием неуравновешенной центробежной силы ∆F2 возникают новые колебания. Суммарная амплитуда при сложении этих колебании может достигнуть нежелательного значения. Во избежание этого, между смежными кривыми вставляют прямолинейный участок такой длины, чтобы колебания, вызванные силой ∆F1, погасли до начала следующей кривой. Существует различие в характере движения поезда по однои разнонаправленным смежным кривым. При движении поезда по кривым направленным в одну сторону, например вправо, при входе на первую кривую вагон под влиянием разностей уровней головок рельсов наклоняется вправо, затем при выходе с первой кривой возвращается в нормальное положение. Во второй кривой вагон вновь дважды меняет направление вращения. При движении по кривым, направленным в разные стороны, вагон после выхода с первой кривой, на которой вращался против часовой стрелки, при входе на вторую кривую продолжает вращаться в том же направлении, т.е. против часовой стрелки. Таким образом при движении по однонаправленным кривым вращение вагона - 4 раза меняет направление, а по разнонаправленным - 3. По этим причинам движение вагона во втором случае более плавно, чем в первом. Поэтому прямая вставка между разнонаправленными кривыми короче, чем при однонаправленных. Например, на линиях II и III категории по СНиП прямая вставка между однонаправленными кривыми должна быть не менее 100 м, а при разнонаправленных – не менее 75 м. В трудных условиях разнонаправленные кривые разрешается проектировать в притык, т.е. без прямой вставки. Переходные кривые на план не наносятся, так как на чертеже они сливаются с круговыми кривыми и прямой. Поэтому при проектировании плана для обеспечения необходимого расстояния между концами круговых кривых с учетом переходных кривых вводится так называемая фиктивная, или строительная вставка (рис. 5). Длина строительной вставки (м) определяется: b l1 / 2 d l 2 / 2 (26) 5. Проектирование плана и его показатели Проектирование плана и его показатели. План в процессе трассирования железнодорожной линии проектируется в обычных условиях в такой последовательности [2]. 1. Руководствуясь правилами, на топографической карте или в плане проводят прямые и определяют углы поворота α (рис. 2,а). 2. Прямые сопрягают круговыми кривыми (рис. 2, б). Радиус каждой кривой R выбирают индивидуально, стандартным как можно большей величины, но не менее регламентированного СНиП. 3. В зависимости от радиуса R категории линии и номера зоны скоростей по СНиП определяют длину переходной кривой l. Номер зоны скоростей устанавливают по кривой скорости, а если ее нет - по очертанию профиля. 4. В сомнительных случаях проверяют достаточность длины круговой кривой между переходными по формуле R / 180 K min l0 5. При близко расположенных круговых кривых проверяют длину строительной вставки по формуле: b l1 / 2 d l2 / 2 а – нанесение прямых; б – вписывание круговых кривых Рисунок 4 - Проектирование плана По готовому проекту плана составляют продольный профиль. На профиле в специальной графе наносят схематический план и выписывают его элементы. Кривые на схематическом плане изображают в виде скобок. Внутри скобки выписывают на профилях: схематическом – радиус R, угол поворота Y, длину круговой кривой K; подробном - радиус R, угол поворота Y длину кривой с учетом переходной К, тангенс Т, длину переходной кривой L. Параметры плана К и Т определяют по таблицам. Длина кривой с учетом переходной равна сумме длин круговой и переходной кривых. Оценивают качество и сравнивают варианты плана по таким показателям: 1) длина кривых ∑К и прямых ∑П, км; 2) процент кривых 100∑К/ ∑П + ∑К; n 3) число кривых на 1 км , кривых /км (n K П – общее число кривых); 4) минимальный радиус кривой Rmin; 5) процент кривых с минимальным радиусом 100Rmin (min) 180 ( K П ) (min) сумма углов поворота кривых с Rmin; 6) средний радиус кривых Rср = 180 К Темы СРС 1. Трасса, ее определение, расположение и построение. 2. Прямые и круговые кривые, определение и расчет. 3. План и профиль участка. Элементы плана. Построение профилей. 4. Переходные кривые, расчет и построение. 5. Смежные кривые, прямые вставки, их назначение и построение. 6. Проектирование плана и его показатели. Рекомендуемая литература 1. Гавриленков А.В., Переселенков Г.С. Изыскания и проектирование железных дорог: Учебник для техникумов. - М.: Транспорт, 1984. -287 с. 2. Кантор И.И, Гулецкий В.В. Основы проектирования и строительства железных дорог. – М.: Транспорт. 1990. – 272 с.