Презентация4_a
реклама

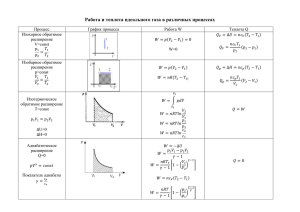
Первое начало термодинамики. Изопроцессы идеального газа Чужков Юрий Петрович Доцент каф. физики, канд.ф.м.н План занятия Изопроцессы идеального газа 1. Изотермический процесс. 2. Изохорный процесс. 3. Изобарный процесс. 4. Адиабатический (адиабатный) процесс. 5. Политропный процесс. 6. Работа, производимая газом (над газом) при различных изопроцессах. Изопроцессы идеального газа Q U A Первое начало термодинамики Q i m RT pdV 2 Процессы, в которых один из трех параметров состояния p,V,T остаются постоянными, называются изопроцессами, масса газа при этом считается неизменной R = 8,31Дж/Кˑмоль Изопроцессы идеального газа Изотермический процесс T = const, pV = const Изотермический процесс – термодинамический процесс, происходящий в физической системе при постоянной температуре. Закон Бойля – Мариотта. К изотермическим процессам относятся, например, кипение жидкости или плавление твердого тела при постоянном давлении. Первый закон термодинамики в изотермическом процессе записывается в виде: Q = A – все тепло, сообщенное системе, идет на совершение работы Внутренняя энергия системы не изменяется p T2>T1 Гипербола P1 const T2 P2 0 T1 V1 V2 pV RT V i m U RT 0 2 Уравнение состояния идеального газа T const p1V1 p2V2 pV const P1 V2 P2 V1 Изотермический процесс T = const Задача 1 В круговом процессе 1-2-3-4 для идеального газа… P 1 4 0 Задача 2 2 3 V 1) T1 > T2 > T4 3) T1 > T4 > T2 2) T2 > T4 > T1 4) T2 > T1 > T4 Объем идеального газа уменьшается при постоянной температуре в 4 раза. Давление газа в сосуде… 1) Увеличилось в 2 раза 3) Уменьшилось в 2 раза 2) Увеличилось в 4 раза 4) Уменьшилось в 4 раза Изотермический процесс T = const Задача 1 В круговом процессе 1-2-3-4 для идеального газа… P 1 4 0 2 3 V 1) T1 > T2 > T4 3) T1 > T4 > T2 2) T2 > T4 > T1 4) T2 > T1 > T4 2) T2 > T4 > T1 Задача 2 Объем идеального газа уменьшается при постоянной температуре в 4 раза. Давление газа в сосуде… 1) Увеличилось в 2 раза 3) Уменьшилось в 2 раза 2) Увеличилось в 4 раза 4) Уменьшилось в 4 раза 2) Увеличилось в 4 раза P1V1 P2V2 V1 P2 V2 P1 Изотермический процесс T = const Задача 3 Азот массой 814 г расширили изотермически при температуре 248 К. Причем объем газа увеличили в 2 раза. Найти изменение внутренней энергии газа. Задача 4 На TV диаграмме показан процесс изменения состояния идеального одноатомного газа. Начальное давление газа равно 106 Па. Количество теплоты, полученное газом, равно 3 кДж. Чему равна работа, совершенная газом? 1) 1 кДж 2) 3 кДж 3) 4 кДж 4) 7 кДж Изотермический процесс T = const Задача 3 U Азот массой 814 г расширили изотермически при температуре 248 К. Причем объем газа увеличили в 2 раза. Найти изменение внутренней энергии газа. i RT 2 Задача 4 T 0 U 0 На TV диаграмме показан процесс изменения состояния идеального одноатомного газа. Начальное давление газа равно 106 Па. Количество теплоты, полученное газом, равно 3 кДж. Чему равна работа, совершенная газом? 1) 1 кДж 2) 3 кДж 2) 3 кДж AQ 3) 4 кДж 4) 7 кДж ИЗОПРОЦЕССЫ ИДЕАЛЬНОГО ГАЗА Изохорный процесс V = const, p/T = const Изохорный процесс – термодинамический процесс, происходящий в физической системе при постоянном объеме. Закон Шарля. i m Q U A Q RT pdV 2 Первое начало термодинамики в изохорном процессе записывается в виде: Q = ∆U, работа A = 0 U – внутренняя энергия А - работа Все тепло, подводимое к системе, идет на изменение внутренней энергии P P i m RT 2 U m CV T V V1 0 U V 0 p1 p 2 T1 T2 V2 > V 1 pV V2 T 0 p1 T1 p 2 T2 T m RT V = const Изохорный процесс V = const Задача 1 Задачи. Тесты. Газообразный водород, находившийся при нормальных условиях в закрытом сосуде объемом 5 л, охладили на 55К, Найти изменение внутренней энергии газа. Дано: p = 105 Па, Е = 273 К, V = 5 ·10-3 м3, ∆T = 55 К, V = const Найти: ∆U U i m RT 2 Решение Водород - двухатомный газ. Число степеней свободы i = 5 кг 3 Молярная масса водорода 2 10 моль Масса газа не дана. pV m RT1 m pV RT1 i pVT U 2 T1 5 10 5 5 10 3 55 U 282 Дж 2 273 Изохорный процесс V = const Задача 2 Задачи. Тесты. При изохорном нагревании азота объемом 10 л давление газа изменилось на ∆p = 0,1 МПа. Определить количество теплоты, сообщенное газу. Дано: V = 10 л, ∆p = 0,1 Мпа, i= 5 Найти : Q Решение Q = ∆U pV A = p∆V = 0 m RT U i Q Vp 2 Ответ: Q = 2,5 кДж i m RT 2 p1V m m p p 2 p1 RT1 p 2V RT2 T T2 T1 5 Q 10 10 3 0,1 10 6 2,5кДж 2 ИЗОПРОЦЕССЫ ИДЕАЛЬНОГО ГАЗА ИЗОБАРНЫЙ ПРОЦЕСС p = const, V/T = const Изобарный процесс - термодинамический процесс, происходящий в физической системе при постоянном давлении. Закон Гей - Люссака. Теплота, переданная системе идет и на увеличение внутренней энергии и на совершение системой работы i m Q RT pdV 2 Объем идеального газа при изобарическом процессе пропорционален температуре V Графики изобарного процесса имеют вид: p V p p1 P2>P1 V/T = const p2 0 V 0 m RT p T 0 T Изобарный процесс p = const Тест 1 Задачи. Тесты. Как изменяется давление данного количества идеального газа при переходе из состояния 1 в состояние 2? RT R p V V 1) Не изменится, 2) Увеличится, 3) Уменьшится, T 4) Ответ неоднозначен V 2 1 0 T Чем круче график (чем больше знаменатель), тем меньше давление Тест 2 Некоторое количество газа, занимающего вначале объем V0 под давлением p0 и при температуре Т0, расширяется один раз изобарически, другой раз изотермически до объема V1. В каком из этих двух случаев газ совершает бо’льшую работу? Изотерма p p0 0 V V0 V1 При постоянном давлении работа, совершаемая газом, равна A = p(V2 - V1). При всех значениях объемов от V0 до V1 давление газа в изобарном процессе будет больше, чем в изотермическом. В соответствии с этим и работа в изобарном процессе будет больше. Изобарный процесс p = const Задача 1 Какое количество теплоты нужно передать ν молям одноатомного газа, чтобы вдвое увеличить его объем в изобарическом процессе, если начальная температура газа Т1? 5 3 V V2 m RT При p = const pV i RT2 T1 RT2 T1 2 Закон Гей - Люссака V1 T1 V 2 T2 5 i2 Q R 2T1 T1 RT1 2 2 Ответ: Q 5 RT1 2 2 )3RT 3 ) RT 4 )5RT 2 i Q RT pV 2 Т1 Т2 T pV Q 1 ) RT 2 Решение V1 0 Задачи. Тесты m RT Q Т2 - ? T2 V2 T V1 i RT RT 2 i2 Q R T 2 V2 = 2V1 (по условию), Т2 = 2Т1 ИЗОПРОЦЕССЫ ИДЕАЛЬНОГО ГАЗА Адиабатический процесс Q = 0 Адиабатический (адиабатный) процесс - процесс, происходящий в физической системе без теплообмена с окружающей средой . При быстром адиабатическом сжатии газ не успевает отдать выделившуюся теплоту и сильно нагревается. Адиабатическое расширение газа вызывает его охлаждение Примером адиабатического процесса могут служить звуковые волны в упругих средах (в частности - в воздухе). Кратковременное открывание клапана сосуда с с газом, находящимся под давлением. Первое начало термодинамики при адиабатическом процессе имеет вид: 0 U A i m RT A 2 Совершение работы сопровождается изменением внутренней энергии Адиабатический процесс Q = 0 m pV RT Уравнение адиабаты (в переменных p,V) pV const Cp CV Показатель адиабаты (коэффициент Пуассона) Cp - молярная теплоемкость при постоянном давлении, C p CV - молярная теплоемкость при постоянном объеме i2 R 2 CV i - число степеней свободы i R 2 График адиабаты (в переменных p,V) имеет вид: P изотерма i2 i TV 1 const Уравнение адиабаты в переменных T, V адиабата 0 V Адиабата идет круче изотермы T p1 const Уравнение адиабаты в переменных p, T i 2 1 Адиабатический процесс Задача 1 1 киломоль азота, находящегося при нормальных условиях, расширяется адиабатически от V1 до V2 = 5V1. Найти изменение внутренней энергии газа. Дано: Ν = 1 кмоль; Азот (N2 ,i = 5); Q = 0; V2 = 5 V1 ; T = 273К; p = 105 Па Найти: ∆U Решение i U RT2 T1 dU A 2 T1V1 1 T2V2 1 i U R0,525 1T1 2 Ответ: T1 V2 T2 V1 T2 найдем из уравнения адиабаты T ,V 1 T1 5 1 T2 Азот -двухатомный газ i =5 , ɣ = 1,4 T2 T1 5 0.4 T1 0,525 5 U 1 8,310,525 1273 2,69 10 6 Дж 2 U 2 ,69 10 6 Дж Адиабатический процесс В цилиндре под поршнем находится кислород массой 0,02 кг при температуре 300 К. Кислород начал расширяться адиабатно, увеличив свой объем в 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в 5 раз. Найти температуру кислорода в конце процесса. Задача 2 Дано: О2 , m = 0,02 кг, T1 = 300К, V2 = 5V1 , адиабата P T1 изотерма T3 0 V 1 Найти: T3 T2 5V1 Решение V T1V1 V T2 T1 1 V2 1 1 1 T2 300 5 T2V2 1 V 1 T1 V2 T2 1 0 ,4 157 K T3 T2 157 K i2 1,4 i ИЗОПРОЦЕССЫ ИДЕАЛЬНОГО ГАЗА Политропный процесс С = const Политропный процесс - термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной Кривая на термодинамических диаграммах, изображающая политропный процесс, называется “политропой” . Для идеального газа уравнение политропы имеет вид: pVn = const n C Cp C CV n -показатель политропы . С - теплоемкость газа в данном процессе, Cp и CV - теплоемкости того же газа, соответственно, при постоянном давлении и постоянном объеме Все рассмотренные ранее процессы являются политропными. - Изотермический n = 1 (pV = const); - Изобарный - Изохорный n = ∞; p 1 / n V 1 2 1 V1 p2 Адиабатный n = 0 (pV0 = p = const) n Показатель адиабаты Политропный процесс Задача 1 Задачи. Тесты. Двухатомный идеальный газ совершает процесс, в ходе которого молярная теплоемкость газа С остается постоянной и равной (7/2)R. Определить показатель политропы этого процесса. Дано: i= 5; C = (7/2)R =const Найти: n Решение. Если молярная теплоемкость в ходе процесса остается постоянной, то имеем дело с политропным процессом. Показатель политропы: n CV i R 2 C Cp C CV Cp и CV - молярные теплоемкости при постоянном давлении и постоянном объеме i2 Cp R 2 Имеем дело с двухатомным газом ( i= 5) 7 Cp R 2 CV 5 R 2 Подставив эти значения в формулу для показателя политропы, найдем искомый показатель политропы : n = 0 Политропный процесс Задача 2 Задачи. Тесты. Некоторый двухатомный газ подвергают политропному сжатию, в результате чего давление газа возросло от p1 = 10кПа до p2 = 30 кПа, , а объем газа уменьшился от V1 = 2,5л до V2 1л. Определить: 1) показатель политропы n; 2) изменение внутренней энергии ∆U газа. Дано: p1 = 10кПа; p2 = 30 кПа, V1 = 2,5л ; V2 1л i=5 Найти: 1) n; 2) ∆U Решение p 2 V1 p1 V2 n Уравнение политропного процесса для двух состояний p2 По условию задачи p 3 1 V1 2,5 V2 Внутренняя энергия газа: U CV T2 T1 pV T1 1 1 R n = 1,2 T2 ,T1 Из уравнения Менделеева - Клапейрона p V T2 2 2 R U Ответ:1) i = 5 3 2,5n p1V1 n p 2V2 n CV p 2V2 p1V1 i 3 p1 3V1 p1V1 8i p1V1 20 p1V1 200 Дж R 2 2 2) U 200 Дж ИЗОПРОЦЕССЫ ИДЕАЛЬНОГО ГАЗА Q dU A Работа идеального газа при изопроцессах 1. Изохорный процесс V = const Работа. A = 0. Тепло. A = 0 Q = dU. Сообщаемое системе тепло превращается в её внутреннюю энергию Внутренняя энергия идеального газа, удалённого от силовых полей, есть средняя суммарная кинетическая энергия всех его молекул. U Wк i i NkT dU NkdT 2 2 i i dU NkdT RdT 2 2 В изохорном процессе единственным способом изменения внутренней энергии системы является теплообмен. Изопроцессы идеального газа Q dU A 2. Изобарный процесс p = const V2 Работа по определению A pdV V1 В изобарном процессе p = const A p( V2 V1 ) pV При изобарном расширении V > 0, и газ совершает положительную работу, тратя на это свою внутреннюю энергию. При изобарном сжатии V < 0, и работа газа отрицательна, то есть работа совершается внешним объектом над газом, и газ при этом получает извне добавку к своей внутренней энергии. Увеличение объёма dV и температуры dT в изобарном процессе связаны уравнением состояния pV = RT . Дифференцируя, получим pdV RdT Работа A RdT Q i i2 RdT RdT RdT 2 2 Работа при изобарном процессе Задача Азот массой 14 г находится при температуре 270 С . В результате изобарного расширения объем газа увеличился в 2 раза. Удельная теплоемкость азота равна 1,05·103 Дж/(кг.К). Определить :1) изменение внутренней энергии газа; 2) работу расширения газа; 3) количество теплоты , сообщенное азоту. Решение T2 U mc T2 T1 P = const Закон Гей - Люссака U mc 2T1 T1 mcT1 V 2 T1 2V1T1 2T1 V1 V1 V1 V 2 T1 T2 U 14 10 3 1,05 10 3 300 4,41кДж Работа A pV2 V1 p2V1 V1 pV1 mRT1 A A 14 10 3 8,31 300 28 10 3 pV 1,25 кДж Ответ:1) ∆U = 4,41кДж; 2) А = 1,25 кДж; m RT V m RT1 p Q U A Q = ( 4,41+1,25)кДж = 5,65 кДж Работа идеального газа при изопроцессах 3. Изотермический процесс T = const V2 Работа по определению: A pdV V1 Для вычисления интеграла необходимо знать выражение для функции p(V). Из уравнения состояния pV = RT получим RT p V V2 A RT V1 V2 dV RT (lnV2 ln V1 ) RT ln V V1 Итак, V2 A RT ln V1 РАБОТА ИДЕАЛЬНОГО ГАЗА ПРИ ИЗОПРОЦЕССАХ 4. Адиабатический процесс Q = 0 Для определения работы надо вычислить интеграл: V2 A pdV V1 Зависимость p(V) следует из уравнения Пуассона γ 1 p1V1 V1 A 1 γ 1 V2 Q dU A pV const γ 1 γ p pV A 1 1 1 2 γ 1 p1 При адиабатном расширении работа положительна (её совершает газ), при сжатии – отрицательна (её совершает над газом внешняя сила). Работа идеального газа при адиабатическом процессе Задача Азот массой 56 г, находящийся в нормальных условиях, расширяется адиабатно, причем объем газа увеличивается в два раза. Определите: 1) изменение внутренней энергии газа; 2) работу расширения газа. Дано: 28 10 3 кг / моль ; m = 56 г(56·10-3 кг); Т = 273К; V2 = 2V1/ Найти: 1) ∆U; 2) А. Решение Cp CV i m U RT2 T1 2 Уравнение Пуассона i2 1,4 i T1V1 1 T2V2 1 V1 T2 T1 V2 1 0 ,4 V 1 5 56 10 3 i m U 8,31 273 1 2,75 кДж U RT1 1 1 2 28 10 3 2 2 V 2 Первое начало термодинамики: Q U A В случае адиабатного процесса Q = 0 A U Ответ: 1) ∆U = - 2,75 кДж; 2) А = 2,75 кДж 1 Спасибо за внимание