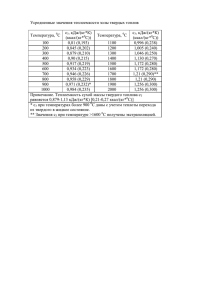
Примеры решения задач по молекулярной физике и
реклама

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ Задача 1 • Котел вместимостью V 2 м3 содержит перегретый водяной пар массой m 10 г при температуре T 300 K . Найти давление пара в котле. • Уравнение Клайперона -Менделеева PV m RT V 2м 2 16 18 г / моль m 10 кг T 300 K P? 3 m RT P V 8,31 500 3 2 18 10 10 1,15 10 6 Па=1,15 МПа Задача 2 • В сосуде вместимостью V=0.01 м3 содержится смесь газов : азота массой m1=7 г и водорода массой m2=1 г при температуре T=280 К. Определить давление смеси газов. V 0,01 м m1 7 г 3 m2 1 г T 280 K P? Закон Дальтона P P1 P2 m1 RT P1 1 V m2 RT P2 2 V RT m1 m2 P V 1 2 RT m1 m2 P V 1 2 8,31 280 7 1 0,01 2 14 2 1 1,74 10 5 Па Задача 3 • В колбе вместимостью V 0,01 м находится кислород при нормальных условиях. Определить: 1) среднюю энергию поступательного движения всех молекул, содержащихся в колбе,2) среднюю энергию вращательного движения одной молекулы 3 Закон равномерного распределения энергии по степеням свободы Для 1 молекулы iпост iвращ 2iколеб 2 kT пост iпост kT 2 3 kT 2 Для всех молекул E N пост N NA m при нормальных условиях 1 моль газа занимает объем Vm=22, 4 л x m молей газа занимает объем V 1 Vm 3 0,01 м x V m V Vm E N пост m 3 N A kT 2 V 3 NA kT Vm 2 0,5 3 23 6,02 10 1,38 10 273 22,4 2 23 75,94 Дж 2) Средняя энергия вращательного движения 1 молекулы вращ 1,38 10 iвращ 23 2 kT kT kT 2 2 273 3,77 10 21 Дж Задача 4 • Вычислить удельные теплоемкости неона и водорода при постоянном объеме и постоянном давлении, принимая их за идеальный газ. Молярные теплоемкости i сv R 2 Для Ne Для H2 i2 сp R 2 i 3 3 сv R 2 5 сp R 2 i 5 5 сv R 2 7 сp R 2 Удельная теплоемкость C сv CV сp C P CV сv CP сp 3 R сv 3R 2 Для Ne CV 2 3 8,31 Дж 623 3 кг К 2 20 10 CP сp 5R 2 5 8,31 2 20 10 3 кДж 1,04 кг К сv 5R CV Для Н2 2 5 8,31 кДж 10,4 3 кг К 2 2 10 сp 7R CP 2 7 8,31 2 2 10 3 кДж 14,5 кг К Задача 5 • Найти удельную теплоемкость CV смеси углекислого газа массой m 3 г и азота 1 массой m2 4 г Q m1 m2 CV T Q Q1 Q2 Q1 m1C1V T Q2 m2C2V T m1 m2 CV T m1C1V T m2C2V T m1C1V m2C2V CV m1 m2 Для СО2 CV 1 сv1 1 6 R R 2 3 1 1 Дж 566,6 3 кг К 12 2 16 10 5 R с Для N2 CV 2 v2 2 2 3 8,31 2 5 8,31 2 2 14 10 3 Дж 742 кг К m1C1V m2C2V CV m1 m2 Дж 3 566.6 4 742 667 кг К 3 4 Задача 6 • Определить количество теплоты, сообщенное кислороду объемом V 20 л , если в процессе изохорного нагревания его давление изменилось на P 100 кПа Первое начало термодинамики Q U A V const A0 Q U mi mi R T2 T1 U RT 2 2 PV 1 m m RT1 P2V m RT2 R T2 T1 P2 P1 V PV i mi Q U RT PV 2 2 5 3 3 100 10 20 10 5 кДж 2 Задача 7 • Азот массой расширяется изобарно . Найти изменение внутренней энергии газа и работу, затраченную на расширение, если сообщенное тепло Q 7 кДж Процесс изобарный, поэтому Q p m c p T2 T1 i 2 m c R p U cV T2 T1 2 i cV R 2 i 5 U cV Q p c p i 2 7 5 U Q p 5 кДж 7 A Q U 7 5 2 кДж Задача 8 • Азот занимает объем V 0,5 м результате адиабатного сжатия давление уменьшилось в 3 раза. Найти конечный объем газа. 3. В Уравнение адиабаты PV 1 1 P2V2 V2 P1 P2 V1 1 P1 P1 V2 V1 V1 P P 2 2 i 2 52 cV i 5 1 5 7 cp 1 V2 0,5 3 5 7 0,228 м 7 5 3