Цель курса:
реклама

Цель курса:
• формирование у учащихся устойчивого интереса к
математике;
• выявление и развитие математических способностей;
• овладение конкретными математическими знаниями,
необходимыми для применения в практической
деятельности;
• интеллектуальное развитие учащихся, формирование
качеств мышления, характерных для математической
деятельности;
• формирование представлений о математике как части
общечеловеческой культуры, понимание значимости
математики для общественного прогресса;
• подготовка к сознательному усвоению систематического
курса алгебры и геометрии;
• ориентация на профессии, существенным образом
связанные с математикой и физикой.
• формировать умения графического решения уравнений
и неравенств, содержащих знак абсолютной величины;
способствовать выбору профиля обучения.
Критериями успешности
занятий будут являться:
• степень развития интереса к
выбранному профилю
• умение преобразовывать выражения с
модулями
• умение строить графики функций и
уравнений с модулями
• умение решать уравнения и
неравенства, содержащие знак
абсолютной величины.
Задачи курса:
• Сформировать у учащихся умения строить графики
функций, содержащих знак абсолютной величины,
методом геометрических преобразований, решать
уравнения и
неравенства с модулями
• Убедить в необходимости владения способами
построения графиков, методом геометрических
преобразований
• Расширить сферу математических знаний учащихся
• Способствовать развитию личной ориентации
учащихся в современном образовательном процессе
• Создать положительную мотивацию обучения.
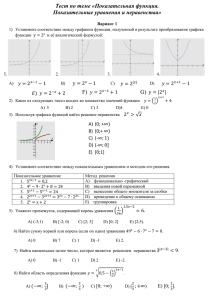
1
Определение, геометрическая
интерпретация понятия модуль
числа
1
Семинар
Отвечают на вопросы учителя,
выполняют необходимые задания,
осуществляют самооценку и
самоанализ результатов
деятельности
2
Графики функций y=¦(х)¦, y=¦(х)¦,
1
Графики функций y=¦(х+а)¦, y=¦
(х)¦+в, y=¦¦¦¦¦х-а¦- в¦- с¦…¦-n¦
1
Урочная форма с
наглядноиллюстративным и
частично-поисковым
методами изучения
Самостоятельная
практическая работа
учащихся
Графики функций y=¦¦(х)¦¦
1
Обсуждают проблему, проводят
анализ условия, выполняют
необходимые задания.
Осуществляют самоконтроль и
корректировку
Самостоятельно строят графики
предложенных функций, оформляют
построение с обоснованием выбора
преобразований
Графики функций ¦y¦=(х), ¦y¦=¦(х)¦
1
Построение различных графиков
функций, аналитическое
выражение которых содержит
знак модуля
3
3
4
5
Уравнения вида ¦(х)¦=a, ¦(х)¦= g(x)
1
Уравнения вида ¦(х)¦=¦g(x)¦
1
Решение уравнений
2
Неравенства вида ¦(х)¦<a, ¦(х)¦>a
1
Неравенства вида ¦(х)¦< g(x) ¦(х)¦>
g(x)
1
Решение неравенств
1
Решение систем неравенств
1
Итоговая самостоятельная работа
1
Урочная форма с
наглядноиллюстративным и
частично-поисковым
методами изучения
Работают с информацией. Проводят
анализ условий. Выполняют
необходимые задания, применяют
нужные преобразования
Работают с информацией. Проводят
анализ условий. Выполняют
необходимые задания, применяют
нужные преобразования для
решения неравенств
Итоговая работа
учащихся как
индивидуальная, так и
групповая
Решают уравнения и неравенства.
Отвечают на вопросы,
осуществляют самоанализ и
самооценку результатов. Участвуют
в коллективном обсуждении
Содержание курса
Абсолютная величина
График функций, содержащих знак
абсолютной величины
Уравнения, содержащие знак
абсолютной величины
Неравенства, содержащие знак
абсолютной величины
Абсолютная величина
Определение
Абсолютной величиной (модулем)
неотрицательного действительного числа а
называют само это число:|a|= a; абсолютной
величиной отрицательного действительного
числа а называют противоположное число:
|а|= -а
Короче это можно записать так:
|а|=
{
а, если а ≥ 0
-а, если а < 0
Например: |8|=8; |-2.65|=2.65
|1-√2|= √2-1
задания
Задачи по теме «Абсолютная
величина»
Найди модуль каждого из чисел:
81; 1.3; -5.2; 8/9; -23/7; -0.012.
2. Напиши все числа имеющие модуль:
26,
5/9; 0; 12.3.
3. Вычисли: |13.8-10|;|√3-5|;|5 -8|+1.2; (1/4)²|1/16-1|.
4. Найти ƒ(1), ƒ(-3), ƒ(0), ƒ(1.4), ƒ(-5), ƒ(2.3)
если ƒ(x)=|2x-3|, ƒ(x)=|x²+3x|, ƒ(x)=|x²6x+8|, ƒ(x)=|x/(x-2)|, ƒ(x)=x²-2|x|, ƒ(x)=(|x|1)(|x|-4), ƒ(x)=(6/|x+2|)-3
1.
График функций, содержащих
знак абсолютной величины
График функций
y=|ƒ(x+a)|, y=|ƒ(x)|+b,
y=|||||x-a|-b|-c|…|-n|
График функций
y=ƒ|(x)|, y=|ƒ(x)|
График функций
y=|ƒ| (x) ||
Задачи для самостоятельного решения
Задания по теме: «График
функций, содержащих знак
абсолютной величины»
Построить график функций:
У=|x+2|+1; y=2-|x-3|;
Y=3+|x|/x; y=x |x|+2
Y=-x/ |x|(x²-4x+5); y=(x|x-1|)/|x|;
Y=||x|-2|-2|; y=||||x|-3|-2|-1|;
Y=0.5|x|-4; y=x²-2|x|;
Y=(3/|x|)-2, y=(|x|-2)/|x|,
Y=|x|³; y=|4-x²|;
Y=|8-6x+x²|; y=|x²-4|x||;
Y=|1-(1/|x|)|; y=||x|³-2|
Уравнения, содержащие знак
абсолютной величины
График уравнения вида
|y|=|ƒ (x)|
Графическое решения уравнений вида
|ƒ (x)|=a,
|ƒ (x)|=g (x)
Задачи для самостоятельного решения
Задания по теме: «Уравнения,
содержащие знак абсолютной
величины»
1.
Построить график уравнения:
|у|=|х|; |y|=|x–3|; |y–1|=|x–2| ;|y|–|x|=2; |x|+|y|=3
2.
Решите графически уравнение:
|x²–2x–3|=3; ||x–1|–1|=2; (|x|+1)²=9; |(x–6)/x|=2; |x|=x+3; |x–3|=(x–3)²;
|х+2|=|2x+1|; |x²–4x–12|=6x–1; x³=|x|; |2x²+5x–3|=|2x–1|
3.
Найти наибольший корень уравнения:
x²+lx-1l=5
4.
Найдите все решения уравнения |x²3x|=a
При каких значениях в уравнение имеет
наибольшее количество корней ||x1|4|=b?
Неравенства, содержащие знак
абсолютной величины
Неравенства вида
|ƒ (x)|<a
|ƒ (x)|>a
Неравенства вида
|ƒ (x)|<g (x)
|ƒ (x)|>g (x)
Задачи для самостоятельного решения
Задания по теме: «Неравенства,
содержащие знак абсолютной
величины»
1.
Решите неравенство:
lx-5|<3; |x+8|>1|x²+4x|<5; |x-2|<|x+4|; |x-2|<4-|x|; |x²4|<O.5x+2; |x²-5x-6|<x+10
2.
Найдите целые решения неравенства:
|x²-1|<9; |x+2|-|x-3|>3
3.
Найти длину наибольшего
промежутка, который является
неравенства 6/(|х-1|-3)>lx+1|
График функции y=ƒ |(x)|
1.
Построить график
функции y=ƒ (x)
при x≥0
2.
Достроить его левую
часть симметрично
правой относительно
оси оу
График функции y=|ƒ (x)|
1.
2.
Построить график
функции y=ƒ (x)
На участках, где
ƒ (x)<0 построить
кривые,
симметричные
построенным
относительно оси ох
График функции y |ƒ (x + a) |
1.
2.
Построить график
функции y=|ƒ (x)|
Осуществить
параллельный перенос
графика функции y=|ƒ
(x)| вдоль оси ох на |а|
единиц масштаба
влево, если а>0,и
вправо, если а <0
График функции y=|ƒ (x) |+b
1.
2.
Построить график
функции y=|ƒ (x)|
Осуществить
параллельный
перенос графика
функции y=|ƒ (x)|
вдоль оси оу на |b|
единиц масштаба
вверх, если а>0,и
вниз, если а <0
График функции
y=|||||x - a|-b |-c|...|-n|
Последовательно выполнить построение
следующих графиков функций
y=|x-a|
y=|x-a|-b
y=|x-a|-b|
y=|x-a|-b| -c
y=|x-a|-b| -c|
……………………..
y=|x-a|-b| -c| -n
y=|x-a|-b| -c| -n|
Построить график функции
y=|||x+2|-1|-3|
График функции y=|ƒ |(x)||
1.
2.
3.
Построить график функции y=ƒ (x)
при x≥0
Достроить его левую часть
симметрично правой относительно
оси оу
Участки графика, расположенные в
нижней полуплоскости, преобразовать
в верхнюю симметрично оси ох
Построить график функции
y=|(|x|-3)²-4|
1.
2.
3.
Построить часть параболы y=x² с вершиной в точке
(3; -4) при x≥0
Достроить левую часть симметрично правой
относительно оси оу
Часть графика, где y<0, преобразовать в верхнюю
полуплоскость симметрично оси ох
График уравнения вида
|y|=|ƒ (x)|
По определению абсолютной величины,
получаем
y=±|ƒ (x)|
Порядок построения |y|=|ƒ (x)|
1.
Построить график функции y=|ƒ (x)|
2.
Построить график функции y=-|ƒ (x)|
( представляет собой кривую,
симметричную графику функции y=|ƒ (x)|
относительно оси ох)
Уравнения вида
|ƒ (x)|=a
1.
2.
3.
4.
5.
Чтобы графически решить уравнение
указанного вида, нужно:
Ввести две функции y=|ƒ (x)| и y=a
Построить график функции y=|ƒ (x)|
Построить график функции y=а
Найти точки пересечения построенных
графиков
Выписать абсциссы найденных точек – это
искомые корни уравнения |ƒ (x)|=a
Уравнения вида
|ƒ (x)|=g (x)
Чтобы графически решить уравнение
указанного вида, нужно:
1.
Ввести две функции y=|ƒ (x)| и g (x)
2.
Построить график функции y=|ƒ (x)|
3.
Построить график функции y= g (x)
4.
Найти точки пересечения построенных
графиков
5.
Выписать абсциссы найденных точек – это
искомые корни уравнения |ƒ (x)|= g (x)
Нервенства вида
|ƒ (x)|<a,| ƒ(x)>a
1.
2.
3.
4.
5.
Чтобы графически решить неравенства указанного
вида, нужно:
Ввести две функции y=|ƒ (x)| и у=а
Построить график функции y=|ƒ (x)|
Построить график функции y= а ( графиком
является прямая параллельная оси ох)
Найти точки пересечения построенных графиков
Выписать в виде числовых промежутков множество
значений переменной х при которых для
неравенства |ƒ (x)|<a график функции y=|ƒ (x)|
расположен ниже прямой y= а, а для неравенства
|ƒ (x)| >a – выше прямой y= а
Неравенства вида
|ƒ (x)|<g (x),| ƒ (x)> g (x)
1.
2.
3.
4.
5.
Чтобы графически решить неравенства указанного
вида, нужно:
Ввести две функции y=|ƒ (x)| и у = g (x)
Построить график функции y=|ƒ (x)|
Построить график функции y=g (x)
Найти точки пересечения построенных графиков
Выписать в виде числовых промежутков множество
значений переменной х при которых для
неравенства |ƒ (x)|< g (x)
график функции y=|ƒ (x)| расположен ниже
графика функции y= g (x), а для неравенства
|ƒ (x)| >g (x)
– выше графика функции y= g (x)
Решить неравенство
|3-|x-2||<1
1.
2.
3.
4.
Введем две функции у =|3|x-2||и у=1
Построим график функции
у =|3-|x-2 ||
(
используя геометрические
преобразования, строим
график за 4 шага)
Построим график функции
y=1
Для всех х из ( -2;0)U (4;6)
график функции у =|3-|x2|| расположен ниже
графика функции у=1
Ответ: ( -2;0)U (4;6)
Решит неравенства
|x²─2x─3|≥x+1
1.
2.
3.
4.
Введем две функции
у=|x²─2x─3|и у = x+1
Построим график функции у
=|x²─2x─3|= |(x─1)²─4|(
используя геометрические
преобразования, строим
график за 2 шага)
Построим график функции y=х
+1
Для всех х из ( -∞;-1)U (1;2)U(4;+ ∞) график
функции у = |x²─2x─3|
расположен выше графика
функции у=х+1, а при х =-1, х
= 4 графики совпадают
Ответ: ( -∞;2] U [ 4;+∞)
Решите уравнение
|x─1|=(x─1) ²
1.
2.
3.
4.
5.
6.
Введем две функции у
=|x─1|и у=(x─1) ²
Построим график
функции у =|x─1|
Построим график
функции у=(x─1) ²
А(0;1) и В(2;1) точки
пересечения
построенных графиков
0 и 2 – корни уравнения
Ответ: 0;2
Решите уравнение
||x+1|─2|=2
Введем две функции
у= ||x+1|─2|и у=2
Построим график
функции
у = ||x+1|─2|
Построим график
функции
у=2
А(-5;2); В(-1;2)и С(3;2)
точки пересечения
построенных графиков
-5;-1 и 3 – корни
уравнения
Ответ: -5; -1; 3
Решите уравнение
|y|=||x|-3|
Порядок построения
заданной функции:
Построить график
функции
у = ||x|─3|
Построить график
функции
у = -||x|─3|