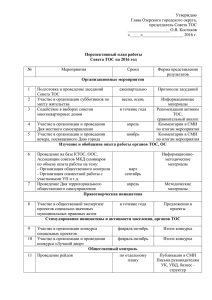
Оценка вероятности сближения (столкновения) контролируемого КА с наблюдаемыми космическими объектами
реклама

Оценка вероятности сближения (столкновения) контролируемого КА с наблюдаемыми космическими объектами А. И. Козориз, В. П. Павлов «Космический мусор» Постановка задачи • Рассчитать вероятность столкновения КА с рассматриваемым «КО риска». • Найти мат. ожидание и СКО вектора минимального расстояния и вектора относительной скорости. • Построить таблицу параметров относительного движения КА и «КО риска» в окрестности ТОС. Исходные данные При наличии прогнозных сообщений При наличии программы измерений • Векторы состояния КА и «КО риска», спрогнозированные с разными интервалами на момент прохождения ТОС. • Радиус сферы, описывающей КА. • Массивы векторов состояния и матриц ошибок КА и «КО риска», спрогнозированные с некоторым шагом на интервал времени, содержащий ТОС. • Радиус сферы, описывающей КА. Критерии достоверности • В случае расчета по прогнозным сообщениям, использовалось, как минимум, три последних сообщения с прогнозами относительного положения МКС и «КО риска». • Последнее из прогнозируемых положений конечной точки вектора относительного положения «КО риска», а также два из трех предыдущих находятся в пределах доверительного интервала 2, в соответствии с требованиями по ошибкам прогнозирования параметров МКС. • Время до наибольшего сближения КО с МКС составляет менее 30 ч. Основные положения • Необходимо определить вектор относительного положения. • Необходимо определить параметры рассеивания конечной точки вектора относительного положения. Задача оценки риска z Эллипсоид (КО) Сфера (КА) y Вектор относительного положения (dr) x Первый метод z 38 30 46 15 Прогнозы положения КО, Взятые с разными интервалами (в часах) 20 54 Среднее 10 КА y x Распределение ошибок прогнозирования для КО № 33246 1 10 ч. 0.8 17 ч. 0.6 P 16 ч. 0.4 11 ч. 34 ч. 0.2 41 ч. 19 ч. 59 ч. 0 -5 0 5 10 15 20 -0.2 r 25 30 35 40 Вычисление ошибок параметров траектории КО СКО параметров траектории КО вычисляются из Правила трех сигм: m где 3 i σ q q qср m i 1 m 1 i qср q m i 1 Разработанные модели ошибок 1. В орбитальной системе координат rnb: r , n , b , r , n , b 2. В элементах орбиты: a , e , i , , , 3. В модифицированных элементах орбиты: T , , , i , , t 1 1 e sin 2 2 e cos Коэффициенты корреляции z rКО КО nКО bКО КА y dr x Вычисление ковариационных матриц вектора состояния КО и КА Матрицы ошибок вычисляются по формулам вида: 0 0 1 1 C (6 6) K (6 6) 0 0 6 6 Для КО формируется усредненная матрица ошибок: 1 C КО (3 3) C КО1 C КО2 C КО3 3 Оценивание средних значений Используется схема Метода Монте-Карло: 1 PC N N P i 1 i Погрешность метода с вероятностью ≈0.9973 не превосходит: DP N 3 N 1 2 Второй метод Dr КА КО t tТОС t tТОС Геометрическая интерпретация dvТОС v КО v КА ξ η dvТОС ζ drξ,η Эллипс КА drТОС drТОС rКО rКА dv ТОС v КО v КА Эллипсоид Испытания методики № № п/п объекта 1 2 3 4 33246 33048 33257 33134 Дата 27.8.2008 30.8.2009 6.9.2009 24.9.2009 Время Интервал (ДМВ) и в часах расстояние в км 21:12:48 1.627 04:09:38 21.173 17:00:29 7.668 13:03:24 20.037 PС PС (ЦУП-Х) (ЦУП-М) 10 1.39·10-2 9.8·10-3 16 0 0 3 1.61·10-15 2.76·10-12 36 2.25·10-22 3.74·10-18