Решение задач В

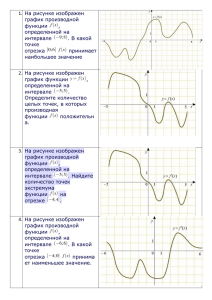
Задачи В 8
ЕГЭ 11 класс
Автор: Удоденко Л.В
Учитель математики
МБОУ РВ(с)ОШ
Задача 1
Прямая
функции
параллельна касательной к графику
. Найдите абсциссу точки касания.
у( х0 )  к
к 7
у  7х  5
у  ( х 2  6 х  8)  2 х  6
2 х0  6  7
2 х0  1
х0  0,5
у  кх  b
0
,
5
Задача 2
Прямая у = -4х-11 является касательной к графику
функции у = х3+7х2+7х-6 . Найдите абсциссу точки касания.
у( х0 )  к
у  4 х  11
к  4
у  ( х 3  7 х 2  7 х  6)  3х 2  14 х  7
у  кх  b
3х 2 0  14 х0  7  4
3х 2 0  14 х0  11  0
2
х01  1 ; х02  3
3
у (1)  4(1)  11  7
у (1)  (1)  7(1)  7(1)  6  7
3
2
- 1
Задача 3
На рисунке изображен график функции
, определенной на
интервале
. Определите количество целых точек, в которых
производная функции положительна.
f ( x)  0
f(x) - возрастает
4
Задача 4
На рисунке изображен график функции
, определенной на
интервале (-5;5) . Определите количество целых точек, в которых
производная функции отрицательна.
f ( x)  0
f(x) - убывает
7
Задача 5
На рисунке изображен график функции
, определенной на интервале
(-5;5) . Определите количество целых точек, в которых касательная к графику
функции параллельна прямой у=6 или совпадает с ней.
4
Задача 6
На рисунке изображен график функции у = f(x) , определенной на
интервале (-2;12). Найдите сумму точек экстремума функции f(x) .
1+2+4+7+9+10+11=44
1 2
4
7 9
10 11
4
4
Задача 7
На рисунке изображен график производной функции f(x) , определенной на
интервале (-8;3) . В какой точке отрезка [-3;2] f(x) принимает наибольшее
значение.
f ( x)  0
f(x) - убывает
х=-3
-3
2
- 3
Задача 8
На рисунке изображен график производной функции , определенной на
интервале (-8;4) . В какой точке отрезка [-7;-3] f(x) принимает
наименьшее значение.
f ( x)  0
f(x) - возрастает
х=-7
-7
-3
- 7
Задача 9
На рисунке изображен график производной функции , определенной на
интервале (-7;4) . В какой точке отрезка [-6;-1] f(x) принимает
наибольшее значение.
х=-1
-6
-1
- 1
Задача 10
На рисунке изображен график производной функции f(x) , определенной на
интервале (-7;14) . Найдите количество точек максимума функции f(x) на
отрезке [-6;9].
производна я меняет
знак с ( ) на () в одной
точе на [-6;9]
-6
9
1
Задача 11
На рисунке изображен график производной функции f(x) , определенной на
интервале (-18;6) . Найдите количество точек минимума функции f(x) на
отрезке [-13;1].
производна я меняет
знак с () на ( ) в одной
точке на [-13;1]
-13
1
1
Задача 12
На рисунке изображен график производной функции f(x) , определенной на
интервале (-11;11) . Найдите количество точек экстремума функции f(x) на
отрезке [-10;10] .
производная меняет
знак с () на ( ) и
с () на (-)
в пяти точках на [-10;10]
-10
10
5
Задача
13
На рисунке изображен график производной функции f(x) , определенной на
интервале (-7;4) . Найдите промежутки возрастания функции f(x) . В
ответе укажите сумму целых точек, входящих в эти промежутки.
f ( x)  0
f(x) - возрастает
функция возрастает
на (-7;-5,5) и (-2,5;4)
-6+(-2)+(-1)+0+1+2+3= -3
-
3
Задача
14
На рисунке изображен график производной функции f(x) , определенной на
интервале (-5;7) . Найдите промежутки убывания функции f(x) . В ответе
укажите сумму целых точек, входящих в эти промежутки.
f ( x)  0
f(x) - убывает
функция убывает
на (-2,5;6,5)
-2+(-1)+0+1+2+3+4+5+6= 18
1
8
Задача
15
На рисунке изображен график производной функции f(x) , определенной на
интервале (-11;3) . Найдите промежутки возрастания функции f(x) . В
ответе укажите длину наибольшего из них.
f ( x)  0
f(x) - возрастает
функция возрастает
на (-11;-10) и (-7;-1) и (2;3)
-1 - (-7)= 6
6
Задача
16
На рисунке изображен график производной функции f(x) , определенной на
интервале (-2;12) . Найдите промежутки убывания функции f(x) . В ответе
укажите длину наибольшего из них.
f ( x)  0
f(x) - убывает
функция убывает
на (-1;5) и (7;11)
5 - (-1)= 6
6
Литература
В работе использованы задачи открытого
банка ЕГЭ по математике . Задачи В8
http://mathege.ru/or/ege/Main