Разные способы решения задач МБОУ СОШ № 1 Учителя математики:
реклама

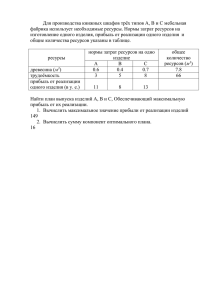
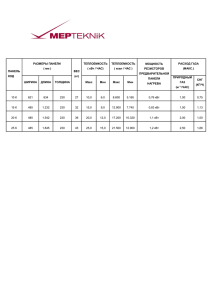
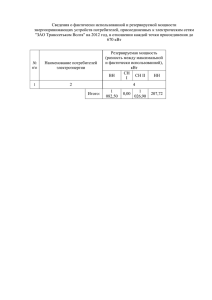
МБОУ СОШ № 1 Разные способы решения задач Учителя математики: Фросина Л.В. Харыбина Е.И. 2 Тема: Цель: обобщить знания о разных способах решения задач; составить алгоритмы решения задач; найти разные способы решения задач. Задачи: закрепление навыка решения разнообразных задач, в том числе задач, требующих поиска способов решения; развитие логического мышления и практических навыков коммуникативного общения учащихся. 1 2 3 4 5 6 7 8 Алгоритм решения задачи по химии Алгоритм решения задачи по математике 1 2 3 4 5 6 7 Внимательно прочитайте условие задачи. Определи, какие величины характеризуют условие задачи. Обозначь неизвестную величину за Х. Составь краткую запись (схему, таблицу) по условию задачи. Составь уравнение и реши его. Проверь, получен ли ответ на поставленный вопрос. Запиши ответ. Решение задачи на сплавы и смеси с точки зрения химии: Дано: m(р-ра)1 = 200 г ω1= 25% = 0,25 m(воды)2 = 75 г ω2 = 28%= 0,28 Решение: m(в-ва)1 = m(р-ра)1* ω1 m(воды)1= m(р-ра)1 – m(в-ва)1 m(воды)общ. = m(воды)1 + m(воды)2 m(в-ва)1= 200г* 0,25 = 50 г m(воды )1= 200г – 50г = 150 г m(сахара) - ? m(воды)общ. = 150г + 75 г = =225 г Составим пропорцию: 225 г - 72% xг - 28% oтсюда, x= 87,5 г (сахара в новом растворе) Найдем количество сахара которое добавили: m(сахара) = 87,5г – 50г = 37,5 г Ответ: m(сахара) = 37,5 г. Решение задачи на сплавы и смеси с точки зрения математики: Решение: Пусть добавили х г сахара. Было Стало Масса 200 г (200 +75 + х) г Конц-я о,25 0,28 Вещество 50 г (50 + х) г 50 + х = 0,28 275 + х 50 +х = 77 + 0,28х х- 0,28х = 27 0,72х = 27 х= 37,5 Ответ: 37,5 г. Алгоритм решения задачи по физике 1 2 3 Вычислить электроэнергию потребляемую каждым прибором в течении месяца по формуле: А = Р ∙ t Вычислить общее потребление электроэнергии всеми приборами в течении месяца по формуле: А= A1 +A2 + A3 + A4 + A5 Вычислить стоимость электроэнергии по формуле: Стоимость = тариф ∙ А Алгоритм решения задачи по математике 1 2 Вычислить общее потребление электроэнергии за месяц всеми приборами Учитывая тариф, вычислите стоимость потребленной электроэнергии Решение задачи с точки зрения физики: Дано: U = 220 B P1 = 40 Bт t1 = 4 ч∙30 P2 = 100 Вт t2 = 6 ч∙30 P3 = 800 Вт t3 = 1 ч∙30 P4 = 1000 Вт t4 = 0,5 ч∙30 P5 = 600 Вт t5 = 0,5 ч∙5 Решение: тариф = 2,5 руб/кВт*ч А1 = P1 ∙ t1 ; A1 = 40*4*30 = 4,8 кВт*ч А2 = P2 ∙ t2 A2 = 100*6*30 = 18 кВт*ч А3 = P3 ∙ t3 A3 = 800*1*30 = 24 кВт*ч А4 = P4 ∙ t4 A4 = 1000*0,5*30 = 15 кВт*ч А5 = P5 ∙ t5 A5 = 600*0,5*5 = 1,5 кВт*ч Стоимость - ? А= A1 +A2 + A3 + A4 + A5 А = 4,8+18+24+15+1,5= 63,3 кВт*ч Стоимость = тариф ∙ А Стоимость = 63,3 * 2,5 = 158,25 рублей Ответ: 158,25 рублей. Решение задачи с точки зрения математики: Решение: 1) (40*4 + 100*6 + 800*1 + +1000*0,5)*30 + 600*0,5*5 = =2060*30 +1500 = =63300(Вт)=63,3 (кВт) 2) 63,3 * 2,5 = 158,25 (рублей) Ответ: 158,25 рублей Алгоритм решения задачи по экономике 1 2 3 4 5 6 Вывод формулы для вычисления объема +f производства в месяц q = π(q) p-υ Вычислить новые переменные затраты на единицу продукции после внедрения новых технологий υ1 = 0,96*v Вычислить новый объем производства после внедрения новых технологий в месяц q1 = 1,06 *q Вычислить новые постоянные расходы в месяц после внедрения новых технологий в месяц f1 = 1,01* f Вычислить операционную прибыль в месяц после внедрения новых технологий π1(q)= q1(р – υ1)- f1 Вычислить экономический эффект после внедрения новых технологий ∆π=π1 - π Алгоритм решения задачи по математике 1 2 Прочитай условие и выбери формулу, которую надо использовать при решении задачи. Определи уравнение или неравенство необходимо решить. 3 Составь неравенство. 4 Подставь числовые данные. 5 Реши неравенство методом интервалов. 6 Выбери ответ о наименьшем месячном объеме производства 7 Учти дополнительные условия по изменению прибыли после внедрения новых технологий. 8 Вычисли экономический эффект. 9 Запиши ответ. Решение задачи с точки зрения экономики: Решение: 1) q = π(q) + f p-υ q = 400000+800000 600-400 =6000 штук 2) υ1 = 0,96*v ; υ1 = 0,96*400=384 рубля 3) q1 = 1,06 *q ; q1 = 1,06*6000= 6360 штук 4) f1 = 1,01* f ; f1= 1,01* 800000=808000 рублей 5) π1(q)= q1(р – υ1)- f1 π1(q)= 6360(600-384)-808000= 565760 рублей 6) ∆π=π1 – π ∆π = 565760 – 400000 = 165760 рублей получена прибыль Решение задачи с точки зрения математики: Решение: 1) q(p-υ)-f >= 400000 q(600-400)-800000>=400000 200q>=1200000 q>=6000 2) 6000+0,06*6000=6360(штук) 3)400-0,64*400 = = 400-16=384(р)переменные затраты 4) 6360*(600-384)-808000(р)расходы предприятия 5) 565760-400000=165760 (р) увеличится прибыль Ответ: 165760 р. Достигли ли мы нашу цель? обобщить знания о разных способах решения задач; составить алгоритмы решения задач; найти разные способы решения задач.