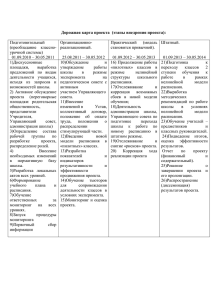
Что такое динамический хаос и зачем он нужен

Что такое
динамический хаос
и зачем он нужен
Динамические системы

+q
v

r
V
-Q

R
p,V,T
1. Некоторый набор переменных однозначно
определяет состояние системы
2. Существует способ по текущему состоянию однозначно найти состояние в любой
последующий момент времени
НЕЛИНЕЙНОСТЬ
линейная система
Δy1
нелинейная система
Δy2
Δy2
Δy1
Δx
Δx
Δy1= Δy2
Δx
Δx
Δ y1≠ Δy2
«Реакция» линейной системы не зависит от
состояния, нелинейной – зависит
Лапласовский детерминизм
• получил формулу для скорости звука в
воздухе
• получил барометрическую формулу с
учетом влажности воздуха
• получил формулу для избыточного
давления под искривленной
поверхностью жидкости (формула
Лапласа)
• выдвинул гипотезу об образовании
Солнечной системы из туманности
вследствие вращения
• показал устойчивость Солнечной
системы в течение очень длительного
времени
Пьер-Симон Лаплас
(1749 – 1827)
• разработал динамическую теорию
приливов
• определили степень сжатия Земли по
неравномерности движения Луны
Лапласовский детерминизм
Мы можем рассматривать настоящее состояние
Вселенной как следствие его прошлого и причину его
будущего. Разум, которому в каждый определенный
момент времени были бы известны все силы,
приводящие природу в движение и положение всех тел, из
которых она состоит, будь он также достаточно
обширен, чтобы подвергнуть эти данные анализу, смог
бы объять единым законом движение величайших тел
Вселенной и мельчайшего атома; для такого разума
ничего не было бы неясного и будущее существовало бы
в его глазах точно так же, как прошлое.
Зная абсолютно точно состояние системы, можно
абсолютно точно предсказать ее состояние в любой
последующий момент времени
Система Лоренца
вязкость
x  ( y  x),
y  rx  y  xz ,
z  bz  xy.
параметр формы
подогрев
x
t
x
t
«Эффект бабочки»
1963: «Deterministic
Nonperiodic Flow»
1972: «Predictability: Does
the Flap of a Butterfly's
Wings in Brazil Set Off a
Tornado in Texas?»
Эдвард Нортон Лоренц
(1917-2008)
Динамический хаос
Ошибка (сколь угодно малая) в начальных
условиях приводит к резкому увеличению ошибки
прогноза за сравнительно небольшое время, делая
прогноз фактически невозможным
Борис Валерианович Георгий Моисеевич
Чириков
Заславский
(1928-2008)
(1928-2008)
Джон Брайан
Тэйлор
«Стандартное отображение»
xn1  xn  pn1
K
pn1  pn  sin 2xn
2
K=0,5
K=1,0
x
x
p
p
Основные вопросы
теоретической нелинейной динамики
Как происходит переход от регулярного
поведения к хаотическому?
Сценарии перехода к хаосу: одни и те же
количественные закономерности для весьма
различных систем.
Что происходит в хаотическом режиме
и как это исследовать? В частности,
есть ли закономерности в хаосе?
Получение характеристик хаотической
динамики, в том числе статистических
Где это встречается?
«Проблема трех тел»
Имеются три тела, взаимодействующие друг
с другом по закону всемирного тяготения.
Необходимо по известным положениям и
скоростям тел рассчитать их траектории.
«Поражаешься сложности этой фигуры, которую я даже не
пытаюсь изобразить. Ничто не является более подходящим,
чтобы дать нам представление о сложности задачи трех
тел…» (Анри Пуанкаре)
«Было бы поистине замечательно, если бы Природа огранила
себя от дальнейшего развития знаний посредством
аналитических трудностей в задачах многих тел» (Макс Борн)
Гидродинамика (турбулентные течения)
Устройства СВЧ-электроники (ЛОВ, ЛБВ, …)
Лазеры
Популяционная биология
Где это можно применить?
(«Какая от этого польза?»)
Подавление хаоса (управление хаосом)
Задача: малым воздействием вернуть систему в
«нормальный» (регулярный) режим.
Генерация сверхширокополосных сигналов
1.Радиолокация
2.Генерация шума
3.Связь на малых расстояниях (беспроводная
техника)
Системы скрытой передачи информации
Реконструкция систем по временным рядам
Биология и
медицина (ЭКГ,
ЭЭГ, …)
Метеорология
Геофизика
Задачи
(сейсморазведка
и т.п.) о системе
Получение информации
(например, (курсы
о числе степеней свободы)
Экономика
валют,
биржевые
Прогноз
поведения системы
индексы, …)
Саратовская группа
теоретической нелинейной динамики
http://sgtnd.narod.ru
Факультет нелинейных процессов СГУ
http://www.sgu.ru/structure/non-linearprocesses
Савин Алексей Владимирович
E-mail: AVSavin@rambler.ru