математика ответыx

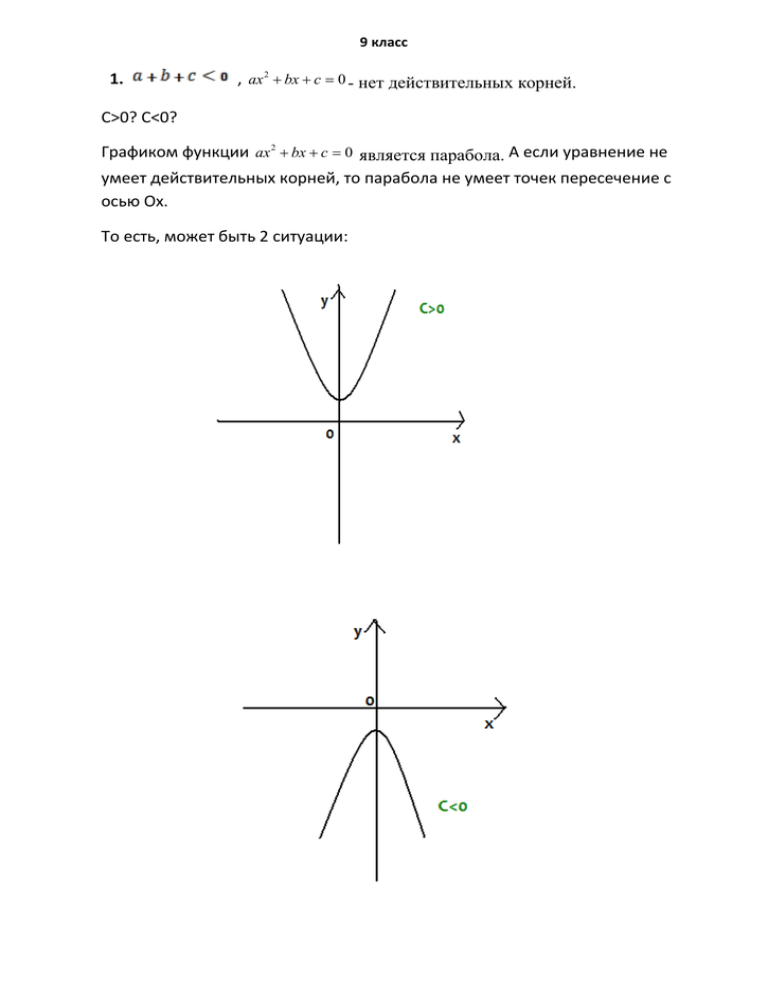
9 класс
1.
, ax 2  bx  c  0 - нет действительных корней.
С>0? C<0?
Графиком функции ax 2  bx  c  0 является парабола. А если уравнение не
умеет действительных корней, то парабола не умеет точек пересечение с
осью Ох.
То есть, может быть 2 ситуации:
ax 2  bx  c  0
2
2
Если, D= b - 4ac <0 , то b < 4ac  b< -(a+c)
Мы знаем, что х  a , то
b  4ac
 4ac  b  4ac

 b  4ac

b  (a  c)
b  (a  c)

-(a+c)  4ac
a+c< -4ac
Для положительного
значения переменной с это
выполнятся не будет,
следовательно,c<0.
Ответ. C<0
2. Целые числа могу быть вида: 3k, 3k+1. 3k-1; где k-целое число.
1) Если среди 5 чисел три больше чисел вида 3k, то сумма любых трех из них
делится на три.
3k+3k+3k=9k
2) Если среди 5 чисел два вида 3k, то оставшиеся три могут быть:
 Три вида 3k+1
 Три вида 3k-1
Тогда если их сложить (3k+1) + (3k-1) +3k = 3k+1+3k-1 +3k= 9k, получаем
искомое.
3) Так же может быть:
 Два вида 3k-1 и один вид 3k+1
 Два вида 3k+1 и один вид 3k-1
То. сложив, тоже получи число, делящееся на 3.
3k + (3k-1)+(3k+1)=9k
4) И даже если, среди 5 чисел 4 вида 3k. То может быть:
 Один вид 3k-1
 Один вид 3k+1
3k + (3k-1)+(3k+1)=9k
Очевидно, что их сумма тоже будет делится на три.
Таким образом, мы рассмотрели все возможные случаи. Значит, мы
доказали , что из любых пяти чисел можно найти три, сумма которых
делится на 3.
x 2  10 x  15
3x

3.
.
x 2  6 x  15 x 2  8 x  15
15
3
x 
15
15
x6
x 8
x
x
x  10 
;
15
15
Мы видим, что в каждой части уравнения есть x- , пусть x- =у
x
x
Тогда уравнение принимает вид:
у  10
3

у6
у 8
3(у-6)=(у-10)*(у-8)
2
3у-18=у -8у-10у+80
2
-у +21у-98=0
2
у -21у+98=0
D= 441-392=49=7
2
у 1 =7; у 2 =14
Значит, 1) x1) x-
15
15
=7 или 2) x- = 14
x
x
15
=7
x
x 2  7 x  15
 0 ; x 0
x
2
x -7x-15=0
D= 49+60=109. Целого корня из данного дискриминанта мы найти не
можем, значит, действительных корней нет.
2) x-
15
= 14
x
x 2  14 x  15
 0; x 0
x
2
x -14x-15=0
2
D= 196+60=225=16
x 1 =15, x 2 =-1.
Таким образом, уравнение имеет два корня: x 1 =15,
x 2 =-1.
Ответ. 15; -1.
4.
( 5 2 6  5 2 6)*
3
.
2
52 6  3
5  2 6  3 5  4  6  3 5  4  6  3 77 67 10






5
2
2
2
2
2
2
2
Ответ. 5
5.
Т.к. возраст дочерей составляет арифметическую прогрессию, разность
которой равна 2. Самая первая дочь старше второй дочери на 2 года,
третью на 4 года, четвертую на 6 лет и пятую, самую младшую на 8 лет.
Т.е. когда самой младшей исполнилось 5 лет, то самой старшей было 13
лет.
Колво
лет
5
лет
7 лет
9 лет
11 лет
13 лет
Всего
книг
Колво
книг
5
5+6+7=18
18+8+9=
35+10+11=
56+12+13=
195
35
56
81
Колво
лет
7
лет
9 лет
11 лет
13 лет
15 лет
Колво
книг
18
35
56
81
81+14+15=110
300
Значит, когда младшей было 7 лет, а старшей домашняя библиотека
составляла 300 книг.
Колво
лет
9
лет
11 лет
13 лет
15 лет
17 лет
Колво
книг
35
56
81
110
110+16+17=
Колво
лет
10
лет
12 лет
14 лет
16 лет
18 лет
Колво
книг
5611=
81-13=68
11015=95
14317=126
143+18=161
425
143
495
45
Значит, когда дочерям было 10,12,14,16,18 лет соответственно, их
домашняя библиотека составляла 495 книг.
Ответ. 10 лет, 12 лет, 14 лет, 16 лет, 18 лет.
6.Пусть
искомое двузначное число 10a+b, тогда по условию должно
выполняться:10a+b=a 2 +2ab+b 2
Подставим по очереди вместо а, числа от 1 до 9. И решим соответствующие
уравнения относительно переменно b, находим
a=1
целых корней нет
a=2
целых корней нет
a=3
целых корней нет
a=4
целых корней нет
a=5
целых корней нет
a=6
целых корней нет
a=7
целых корней нет
a=8
Значит, искомое число 81.
Проверим: 8+1= 81 , 9=9. Верно.
Ответ. 81
8. 7
99
9
.
Возведем число 7 в степень от 1 до 9, и попытаемся найти определенную
последовательность.
7 1 =7
7 2 =49
7 3 =343
7 4 =2401
7 5 =16807
7 6 =117649
7 7 =823543
7 8 =5764801
7 9 =40353607
Мы заметили, что возводя число 7 в степени, есть определенна
последовательность – 49,43,01,07,,49,43,01,07…
Значит, две последние цифры числа 7 - 07, то и число
цифры – 07.
9
7
99
9
на конце имеет
Ответ. 07
x3  5 x 2  4 x  20
9.
x 2  3x  10
x 2 +3x-10=0
D=9+40=49=7 2 , x 1 =2, x 2 =-5


x2 x  5  4x  5 x  5  x2  4 x  2  x  2


 x2
x  2  x  5 x  2  x  5
x2
10.Люди могут быть знакомыми или не знакомыми, третьего не дано.
Пусть, знакомые это З, а незнакомые это Н.
Тогда, между 6 людьми могут быть такие комбинации:
ЗЗЗЗЗЗ
НННННН
НННЗЗЗ
ННЗЗЗЗ
ЗЗНННН
ЗННННН
НЗЗЗЗЗ
Конечно, один знакомый среди не знакомых быть не может. Значит, или
все знакомы, или знакомы 2ое, 3ое, 4о,5о, или же все друг друга знают.
Если хотя бы 2 человека знакомы или незнакомы хотя бы с 3мя из них, и
пусть хотя бы 2 из них находятся в таком же отношении, то они вместе
образуют искомую тройку : знакомы или незнакомых людей. Ч.т.д.