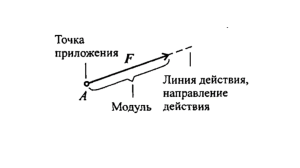
Пример решения контрольной задачи на принцип возможных
реклама
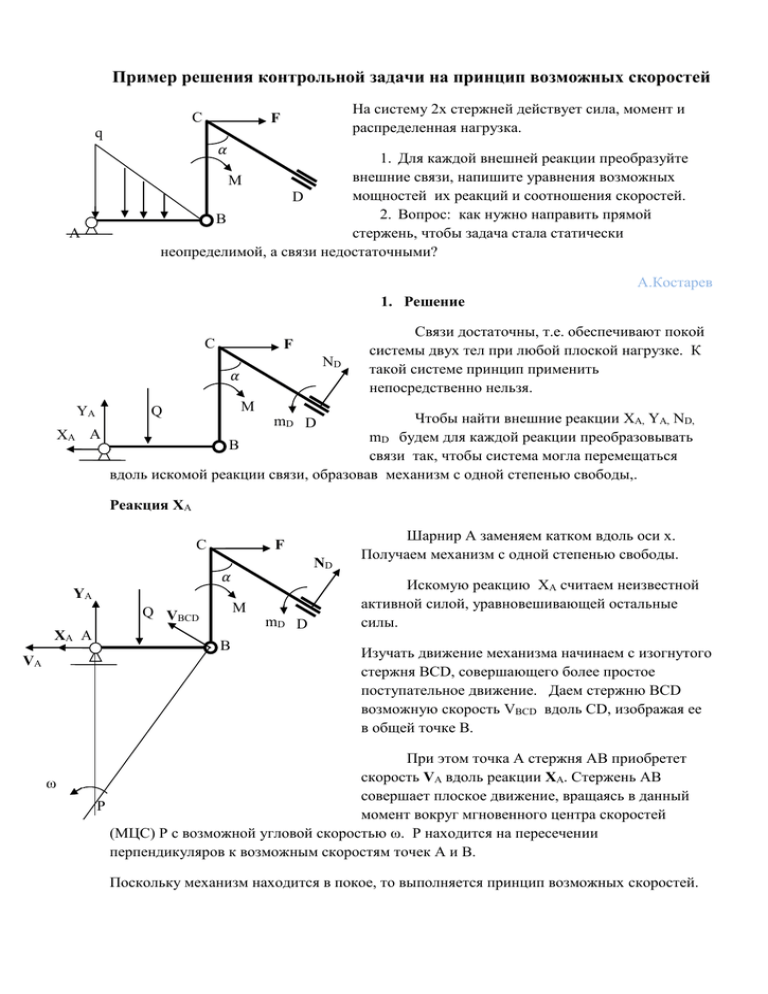
Пример решения контрольной задачи на принцип возможных скоростей C На систему 2х стержней действует сила, момент и распределенная нагрузка. F q 𝛼 1. Для каждой внешней реакции преобразуйте внешние связи, напишите уравнения возможных M мощностей их реакций и соотношения скоростей. D 2. Вопрос: как нужно направить прямой B стержень, чтобы задача стала статически неопределимой, а связи недостаточными? A А.Костарев 1. Решение C F ND 𝛼 YA XA M Q A A Связи достаточны, т.е. обеспечивают покой системы двух тел при любой плоской нагрузке. К такой системе принцип применить непосредственно нельзя. Чтобы найти внешние реакции XA, YA, ND, mD будем для каждой реакции преобразовывать B связи так, чтобы система могла перемещаться вдоль искомой реакции связи, образовав механизм с одной степенью свободы,. mD D Реакция XA C F ND 𝛼 A YA M Q VBCD XA A VA ω mD D B Шарнир А заменяем катком вдоль оси х. Получаем механизм с одной степенью свободы. Искомую реакцию XA считаем неизвестной активной силой, уравновешивающей остальные силы. Изучать движение механизма начинаем с изогнутого стержня BCD, совершающего более простое поступательное движение. Даем стержню BCD возможную скорость VBCD вдоль CD, изображая ее в общей точке В. При этом точка А стержня АВ приобретет скорость VA вдоль реакции XA. Стержень АВ совершает плоское движение, вращаясь в данный P момент вокруг мгновенного центра скоростей (МЦС) Р с возможной угловой скоростью ω. Р находится на пересечении перпендикуляров к возможным скоростям точек А и В. Поскольку механизм находится в покое, то выполняется принцип возможных скоростей. Приравниваем нулю возможную мощность всех активных сил. Мощность сил, приложенных к стержню АВ в плоском движении, вычисляем как произведение момента силы на угловую скорость стержня ω 𝑋𝐴 𝐴𝑃𝜔 − 𝑄 Кинематическая связь: 𝐴𝐵 𝜔 − 𝐹𝑉𝐵𝐶𝐷 𝑆𝑖𝑛 ∝= 0 3 𝐴𝐵 , 𝐶𝑜𝑠 ∝ оставляет в уравнении одну неизвестную XA. 𝑉𝐵𝐶𝐷 = 𝜔ВР, 𝐵𝑃 = 1 𝐴𝑃 = 𝐴𝐵𝑡𝑔 ∝ , 𝑄 = 𝑞𝐴𝐵 2 Реакция YA Шарнир А заменяем катком вдоль оси у. C F ND 𝛼 YA Q XA 𝛼 ω A M mD D A B P Даем шарниру А возможную скорость VA вдоль оси у. Скорость шарнира В может быть направлена только вдоль СD, поэтому МЦС стержня АВ находится в точке В. Это значит, что стержень ВСD неподвижен, а стержень АВ вращается вокруг В с возможной угловой скоростью 𝜔. VA Приравниваем нулю возможную мощность всех сил, приложенных к стержню АВ, вычисленную как произведение момента силы относительно В на угловую скорость стержня ω. −𝑌𝐴 𝐴𝐵𝜔 + 𝑄 Это уравнение определяет реакцию 𝑌𝐴 . 2𝐴𝐵 𝜔=0 3 А.Костарев Реакция mD Скользящую заделку D ставим на шарнир, давая возможность поворота вокруг ND D. 𝛼 A Стержень АВ совершает вращение YA вокруг А. Даем ему возможную угловую M mD Q D скорость 𝜔. Общая точка B приобретает XA A ω BCD возможную скорость VB. B P Скорость точки D направлена вдоль ωAB CD, поэтому стержень в плоском движении VB совершает вращение вокруг МЦС Р с возможной угловой скоростью 𝜔𝐵𝐶𝐷 . Ее направление определено скоростью VB. Приравниваем нулю возможную мощность всех сил. Мощность сил вычисляем как произведение момента относительно их центров скоростей А и Р соответственно на угловые скорости стержней. 𝐴𝐵 𝑄 𝜔 + (𝑚𝐷 − 𝐹𝐶𝐵 − 𝑀)𝜔𝐵𝐶𝐷 = 0 3 𝐴𝐵 C F Связь скоростей 𝜔𝐴𝐵 и 𝜔𝐵𝐶𝐷 находим через выражение скорости 𝑉𝐵 общей точки В: 𝑉𝐵 = 𝐴𝐵𝜔𝐴𝐵 = 𝐵𝑃𝜔𝐵𝐶𝐷 , 𝐵𝑃 = 𝐶𝐷𝑆𝑖𝑛 ∝ −(𝐵𝐶 − 𝐶𝐷𝐶𝑜𝑠 ∝)𝐶𝑡𝑔 ∝ , Подстановка связи скоростей в уравнение мощностей позволяет найти момент реакции mD Реакция ND Скользящую заделку D заменяем двойной скользящей заделкой, которая позволяет стержню BCD двигаться произвольно, но C F только поступательно. Направление ND поступательного движения задает общий 𝛼 mD A шарнир В. YA M Q Даем стержню АВ возможную угловую D XA A скорость 𝜔 вокруг шарнира А. Возможные B VВ скорости всех точек стержня BCD одинаковы ω и равны VВ. VВ Приравниваем нулю возможную мощность всех активных сил. Мощность сил, приложенных к стержню АВ в его вращении вокруг А вычисляем как произведение момента на угловую скорость стержня ω. Искомая реакция ND создает мощность на скорости VВ −𝑁𝐷 𝑉𝐵 𝑆𝑖𝑛 ∝ +𝑄 Кинематическая связь: 𝐴𝐵 𝜔=0 3 𝑉𝐵 = 𝐴𝐵𝜔 Подстановка связи скоростей в уравнение мощностей позволяет найти реакцию 𝑁𝐷 А.Костарев 2. Ответ на вопрос Перпендикулярно CD. Здесь следует исходить из факта, что при правильном числе неизвестных, как только связи становятся избыточными в одном направлении, они становятся недостаточными в другом направлении. Если стержень АВ перпендикулярен CD, то появляется свобода перемещения стержня BCD вдоль CD. Одновременно связи будут избыточными по направлению АВ.