Кинематический анализ кулисного механизма
реклама
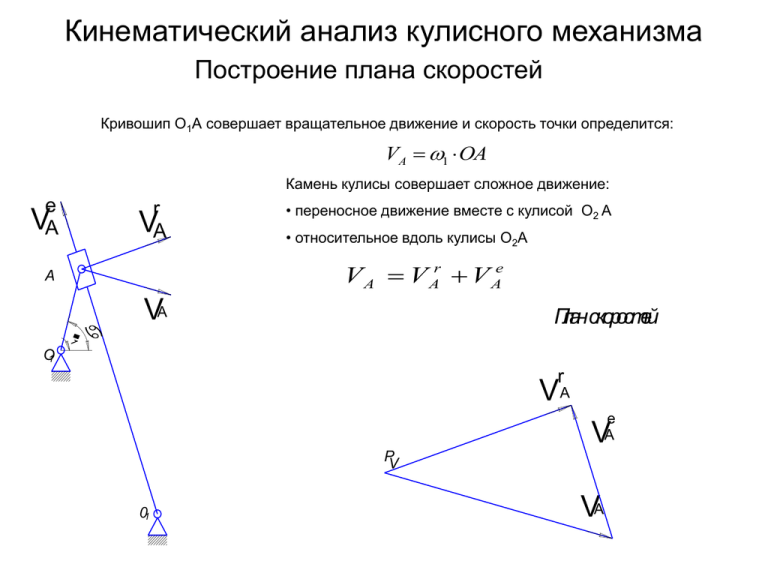
Кинематический анализ кулисного механизма Построение плана скоростей Кривошип О1А совершает вращательное движение и скорость точки определится: VA 1 OA Камень кулисы совершает сложное движение: e VA r VA • переносное движение вместе с кулисой О2 А • относительное вдоль кулисы О2А V A V Ar V Ae A VA Планскоростей O1 r VA e A V PV 01 VA Построение плана ускорений Ускорение точки А звена 2 (кривошип), из условия, что кривошип вращается с постоянной угловой скоростью и касательные ускорения отсутствуют: e aА3,А4 t к aA3 aA4 Масштаб построений плана ускорений, приняв длину отрезка на плане ускорений соответствующее нормальному ускорению точки А V A22 lО1 A а а Аn 2 ра а Ускорение точки А звена 3 (камень кулисы). Для определения запишем векторное уравнение для случая, когда звено совершает сложное движение: A n аA2 O1 а n A2 План ускорений а A3 а Aк3 а An4 а At 4 а Ae3, А4 а An2 n aA4 n аA 4 V r A3 2 n aA4 lO 2 A Ускорение Кориолиса aA4 к r аA 3 2 4V A 3 01 Pа Нормальное ускорение при переносном движении Касательное ускорение звена 4 а tА4 направлено перпендикулярно кулисе Относительное ускорение аА3, А4 направлено вдоль кулисы t aA4 e aA3,А4 к aA3 n аA2 а План скоростей рычажного механизма Ведущее звено (кривошипа) совершает вращательное движение относительно О и окружная скорость равна VВA VВ VA 1 OA Направлена перпендикулярно кривошипу ОА A План скоростей В VA kV O1 VA pV a b VВ VВA 02 Спарринг АВ совершает плоскопараллельное движение и векторное уравнение для определения скорости точки В запишется в следующем виде V B V A V BA Для скоростей VВА и VВ известно только направление PV • VВ - направлена перпендикулярно 02В; •VВА направлена перпендикулярно звену АВ) VA a План ускорений рычажного механизма t aВ a An 2 lOA t n aВA A aВA В n Ускорение точки В определится из векторного уравнения n aB aBn atB a An aBA atBA O1 План ускорений n aВ Нормальное ускорение точки В 02 Pа n aВ aВ t аA aВA a Bn t aВ VB l02B Известны направление ускорения аnВА - оно направлено вдоль спарринга АВ из точки В к точке А, и его величина n a BA n aВA VA2 lOA Нормальное ускорение направлено из точки к центру вращения aA n aВA Нормальное ускорение ведущего звена 2 VBA l AB Для ускорений аtВА и аB известно только направление. • Первое из них направлено перпендикулярно спаррингу АВ • второе перпендикулярно 02В Точка пересечения этих векторов и будет являться точкой b