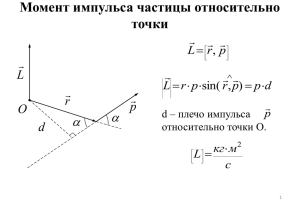
З Д Р А В С Т В У Й...

З Д Р А В С Т В У Й Т Е!
ТЕСТИРОВАНИЕ
Дата
Время
Аудит./Корп.
22.04.04
10
16
307/10
22 апреля
5-я пара
10
03.06.04
16
3 июня
5-я пара
307 ауд.10 корп.
307/10
307 ауд.10 корп.
Лекция 8.
ПРИМЕНЕНИЕ ЗАКОНОВ
СОХРАНЕНИЯ
1. Импульс силы.
2. Удар абсолютно упругих и неупругих
тел.
3. Уравнение движения системы с
переменной массой.
4. Законы сохранения и их связь с
симметрией пространства-времени.
1. ИМПУЛЬС
СИЛЫ
Примером применения законов сохранения импульса и энергии при
решении реальной физической задачи является удар абсолютно
упругих и неупругих тел.
Удар (или соударение) – это столкновение двух или
более тел, при котором
взаимодействие длится очень
короткое время.
Помимо ударов в прямом смысле этого слова (столкновение атомов
или бильярдных шаров), сюда можно отнести и такие, как удар
человека о землю при прыжках с балкона в известных анекдотах и
т.д.
Силы взаимодействия между сталкивающимися телами
(ударные или мгновенные силы) столь велики, что
внешними силами, действующими на них можно
пренебречь.
F
<F>
tн
Рис. 8.1
tк
Это позволяет систему тел, в
процессе
их
соударения,
приближенно рассматривать как
замкнутую систему и применять к
ней законы сохранения.
Когда происходит столкновение
между простыми телами, сила
взаимодействия за очень короткое
время обычно нарастает от нулевого
значения в момент контакта до
очень большой величины, а затем
вновь резко спадает до нулевого
значения.
На рисунке 8.1. приведена типичная зависимость величины силы, с
которой одно тело действует на другое при столкновении, от времени. В
интервал времени t = tк – tн, где tн - “ начальный” момент времени (когда
начала действовать сила) и tк – “конечный” момент времени (когда сила
перестала действовать), обычно можно определить с большой точностью
(как правило, он очень короткий).
Из второго закона следует, что результирующая сила,
действующая на тело, равна скорости изменения его

импульса: dp

F
(эта формула применима к
dt
каждому из участвующих в столкновении тел). В течение
бесконечно малого временного интервала dt импульс

изменяется на величину dp  Fdt . Проинтегрировав это
равенство по времени в течение которого проходит
столкновение, получим:   t 
p к  p н   Fdt
 
p
, где к и pн –
t
импульсы тела соответственно перед столкновением и
после него. Интеграл от силы по времени в течение
которого она действует, называется ИМПУЛЬСОМ
t


СИЛЫ:
К
Н
2
I   Fdt
t1
Таким образом, изменение импульса тела равно импульсу
t
силы, действующей на него: p  p  p  F dt (8.1)
К
к
н

tН
Единицы измерения импульса силы и импульса тела совпадают, т.е.
в системе СИ мы имеем единицы кгм/с (или Н/с). Поскольку
 t2 
I   Fdt
импульс силы
равен площади под кривой, описывающей
t

зависимость величины силы F от t (рис. 8.1), формула (8.1)

справедлива, только, если сила F есть равнодействующая всех
сил, действующих на тело. Она справедлива для любой
равнодействующей силы F , причем импульсы pн и pк точно
соответствуют моментам времени tн и tк. В некоторых случаях
удобно использовать среднюю силу Fср, действующую во время
столкновения. Она определяется как такая постоянная сила, которая
действует в течение того же промежутка времени t=tк-tн, что и
реальная сила, создает тот же импульс силы и, следовательно, тоже
изменение импульса.
1
 t2 
Таким образом, I   Fdt .
t1
На рис. 8.1 указали величину средней силы, соответствующей
импульсной силе. Площадь прямоугольника Fсрt равна площади
под кривой, описывающей зависимость импульса силы от времени.
2. УДАР АБСОЛЮТНО УПРУГИХ ТЕЛ
Применим теперь законы сохранения энергии и импульса к лобовому упругому и
неупругому удару. Тела во время удара претерпевают деформацию. Сущность
удара заключается в том, что кинетическая энергия относительного движения
соударяющихся тел на короткое время преобразуется в энергию упругой
деформации. Во время удара происходит перераспределение энергии между
соударяющимися телами. Наблюдения показывают, что относительная скорость
тел после удара не достигает своего прежнего значения. Это объясняется тем, что
нет идеально упругих тел и идеально гладких поверхностей. Отношение
нормальных составляющих относительной скорости тел после и до удара
называется коэффициентом восстановления k: k  V ' / V
n
n
Если для сталкивающихся тел k=0, то такие тела
называются абсолютно неупругими, если k=1 – абсолютно
упругими. На практике для тел 0 < k <1 (например, для
стальных шаров k ≈ 0,56, для шаров из слоновой кости k
≈ 0,89, для свинца k ≈ 0). Однако в некоторых случаях
тела можно рассматривать с большой степенью точности
как абсолютно упругие, либо как абсолютно неупругие.
Прямая, проходящая через точку соприкосновения тел и
нормальная к поверхности их соприкосновения,
называется
линией
удара.
Удар
называется
центральным, если тела до удара движутся вдоль
прямой, проходящей через их центр масс. Мы будем
рассматривать только центральные абсолютно упругие и
абсолютно неупругие удары.
8.1.а). Абсолютно упругий удар – столкновение двух тел, в
результате которого в обоих взаимодействующих телах не
остается никаких деформаций и кинетическая энергия,
которой обладали тела до удара, после удара снова
превращается в кинетическую энергию (это идеальный
случай). Для абсолютно упругого удара
выполняется закон сохранения импульса и
закон сохранения кинетической энергии.
Обозначим скорости частиц до удара через V1 и V2, а
после удара V1' и V2' . При любом значении V>0 частица
движется вправо (координата х возрастает), в то время
как при V<0 частица движется влево и координата х
уменьшается.
Напоминаю,
мы
рассматриваем
центральный удар.
y
1
При указанных допущениях
законы сохранения имеют
вид: m1V1  m2V2  m1V1|  m2V2|
З.С.И.
(8.2)
1
m1
m2
2
2
|2
m1V1
m2V2
m1V1
m2V2



2
2
2
2
x
З.С.К.Э.
(8.3) или
m1 (V1  V )  m2 (V2  V2 )
|
1
|
m1 (V1  V )  m2 (V2  V2 )
2
|
|2
1
|
|2
|
2
|
m1 (V1  V1 )(V1  V1 )  m2 (V2  V2 )(V2  V2 )
Разделив (8.6) на (8.5), получим
(8.4)
(8.5)
(8.6)
|2
|
1
|
|
| (8.7)
или
V1  V2  V2  V1
V1  V  V2  V2
Итак, мы получили, что относительная скорость двух
частиц после столкновения в точности равна их
относительной скорости до столкновения; это верно для
любого лобового удара, независимо от того, какие массы
имеют частицы.
Разберем несколько примеров
1.Частицы с одинаковыми массами. Из закона сохранения
импульса имеем
а) .V1  V2  V1|  V2| Поскольку неизвестных величин две, необходимо
еще одно уравнение. Можно использовать закон сохранения
кинетической энергии, но проще применить уравнение (8.7),
согласно которому, относительные скорости до и после
столкновения одинаковы:
|
|
б) . V1  V2  V2  V1 . Сумма а) и б) дает V1  V2| , а разность а)
и б) дает V  V , таким образом, в результате столкновения
частицы “обмениваются” скоростями; частица 2
приобретает скорость частицы 1, и наоборот. Если частица
2 первоначально покоилась (V2=0), то мы имеем
|
|
V2  V1 , V1  0 .
2. Частица 2 первоначально покоилась (V2=0). Объединяя
V
уравнение сохранения импульсов
с полученными выше
соотношениями для V2 | и V1| , получаем:
|
|
 m  m2 
 2m1 
,
(8.8)

V V  1

V V 
|
1
2
|
2
2
1
m m 
2 
 1
1
1
m m 
2 
 1
Представляют интерес некоторые частные случаи:
а) V2=0, m1=m2. Здесь мы имеем V  V и V1|  0
случай мы уже рассматривали.
|
2
2
. Этот
б) V2=0, m1>>m2. Это случай, когда очень массивная
частица налетает на легкую покоящуюся частицу.
Используя (8.8) имеем, V2 |  2V1 , V1|  V1 . Таким образом,
скорость массивной частицы практически не меняется, а
скорость легкой становится равной удвоенной скорости
налетающей частицы.
в) V2  0 , m1  m2 .Движущееся легкое тело сталкивается с
очень массивным покоящимся телом. Из (8.8) имеем:
m1  m2 , V1|  V1 . Массивное тело практически остается в
покое, тогда как очень легкое тело отскакивает
практически с той же по величине (но противоположно
направленной) скоростью.
г) V2=0, m1>m2. Первый шар продолжает двигаться в том
же направлении, как и до удара, но с меньшей скоростью
V  V  . Скорость второго шара после удара больше, чем
|
1
1
скорость первого после удара V2  V1 .
д) V2=0, m1<m2. Направление удара первого шара
изменяется – шар отскакивает обратно. Второй шар
движется в ту же сторону, в которую двигался первый шар
|
|
V).

V
до удара, но с меньшей скоростью, т.е. (
2
1
9.2.б). Абсолютно неупругий удар – столкновение двух
тел, в результате которого тела объединяются, двигаясь
дальше как единое целое. V  V 
Продемонстрировать абсолютно неупругий удар можно с
помощью шаров из пластилина (глины), движущихся
навстречу друг другу.


Если массы шаров m1 и m2, их скорости до удара Vи1 ,Vто
2
используя закон сохранения импульса, можно записать




m1V1  m2V2  (m1  m2 )V , где V - скорость движения шаров
после удара. Тогда:
|
1
1


 m1V1  m2V2
V
m1  m2
(8.9) Если шары двигались навстречу
друг другу, то они вместе будут продолжать двигаться в ту
сторону, в которую двигался шар, обладающий большим
импульсом. В частном случае, если массы шаров равны

 
(m1=m2), то
V  (V . V ) / 2
1
2
Выясним, как меняется кинетическая энергия шаров при
центральном абсолютно неупругом ударе. Т.к. в процессе
соударения шаров между ними действуют силы, зависящие не от
самих деформаций, а от их скоростей, то мы имеем дело с силами,
подобными силам трения, поэтому закон сохранения механической
энергии не должен соблюдаться. Вследствие деформации
происходит “потеря” кинетической энергии , перешедшей в
тепловую или другие формы энергии. Эту “потерю” можно
определить по разности кинетических энергий до и после удара:
 m1V1 2 m2V2 2  m1  m2 V 2

T  


2
2
2


Используя (8.9), получаем
m1 m2
V1  V2 2
T 
2m1  m2 
Если ударяемое тело было первоначально неподвижно
2
(V2=0), то
.
m1V1 ,
m2 m1V1
V
T 
m1  m2
m1  m2 2
Когда m2>>m1 (масса неподвижного тела очень большая), то
V<<V1 и почти вся кинетическая энергия при ударе переходит в
другие формы энергии. Поэтому, например, для получения
значительной деформации наковальня должна быть массивнее
молотка.
Когда m1>>m2, тогда V≈V1 и практически вся энергия
затрачивается на возможно большее перемещение, а не на
остаточную деформацию (пример, молоток - гвоздь).
Абсолютно неупругий удар – пример того, как происходит
“потеря” механической энергии под действием диссипативных сил.
3. УРАВНЕНИЕ ДВИЖЕНИЯ С
ПЕРЕМЕННОЙ МАССОЙ
Рассмотрим теперь системы, массы которых изменяются.
Такие системы можно рассматривать как своего рода
неупругое столкновение. В этом случае
всего
 проще

обратиться к формуле из пятой лекции: P  MVц . м. , (8.10)
полный импульс системы частицы равен произведению
полной массы системы М и скорости Ц.М. системы. Если
продифференцировав обе части равенства
(8.10) по
времени, то при условии, что М постоянна, получим:



dVц. м.
dP
(8.11)
M
 Ma
 F
dt
dt
ц.м.
внешн.

где Fвнешн. - внешняя результирующая сила, приложенная
к системе. Необходимо очень тщательно
Необходимо очень тщательно определять систему и
учитывать все изменения ее импульса. Важным примером
систем с переменной массой являются ракеты, которые
движутся вперед за счет выбрасывания назад сгоревших
газов; при этом ракета ускоряется силой, действующей на
нее со стороны газов. Масса М ракеты все время
уменьшается, т.е. dM/dt<0. Другим примером систем с
переменной массой представляет собой погрузка сыпучих
или иных материалов на транспортную ленту конвейера;
при этом масса М нагруженного конвейера возрастает, т.е.
dM/dt>0.
dM
М
а) в момент времени t
M+dM
V+dV
б) в момент времени t+dt
Рис.8.2
Общий случай
системы с
переменной
массой
можно
исследовать на примере cистемы,
изображенной на рис. 8.2. В
некоторый момент времени t
система имеет массу М и импульс

MV ; по направлению к ней

движется со скоростью U
небольшое (бесконечно малое)
тело тело массой dM, которое
находится в состоянии, близком к
тому,
чтобы
войти
в
рассматриваемую систему. Для
простоты будем называть этот
процесс “столкновением”.
За бесконечно малый промежуток времени dt к массе
системы М добавляется масса dМ. Таким образом, через
время dt масса системы изменится от М до М+dМ.
(заметим, что масса dМ может быть отрицательной
величиной, например для ракеты, летящей вперед за счет
выброшенных газов). Для того, чтобы применить формулу
(8.11),
необходимо
рассмотреть
определенную
фиксированную систему частиц. Иными словами,
изменение импульса мы должны рассматривать у одних и
тех же частиц как до столкновения так и после него.
Полную систему мы определим как включающую в себя
массы М и dМ. Тогда в исходном состоянии, т.е. в момент
 
времени t, ее полный импульс равен MV  UdM . В момент
времени t+dt (после того как масса dМ присоединилась к
массе
М)

 скорость системы в целом становится равной
V  dV
изменение импульса

dP
запишется в виде:



 
 
 
dP  (M  dM )(V  dV)  (MV  UdM )  MdV  VdM  dMdV  UdM
При этом в соответствии с формулой (8.11) имеем

 


dP MdV  VdM  UdM
Fвнешн. 

dt
dt
, или


dV   dM
Fвнешн.  M
 ( U  V)
dt
dt (8.12,a) 
При написании этой формулы мы опустили слагаемое dMdV,
dt
поскольку в пределе бесконечно малых
величин оно равно
 
Uесть
 V не что иное, как
нулю. Заметим, что разность

скорость
тела массой
dM относительно скорости тела
Vотн

 
Vотнскорость
 UV с
массой М. Таким образом,
- это
которой масса dM входит в систему с точки зрения
наблюдателя, связанного с массой М.
Уравнение (8.12,а) можно записать теперь в виде:

 dM
dV 
M
 Fвнешн.  Vотн.
(8.12,б)
dt
dt

Первое слагаемое в правой части Fвнеш описывает внешнюю силу,
действующую на систему в целом (в случае ракеты в нее следует
включать силу тяжести и силу сопротивления воздуха). В нее не
входит сила, с которой тело массой dM действует на тело массой М
в результате их столкновения, поскольку для системы в целом
(полной системы),
 эта сила является внутренней. Второе слагаемое
в правой части Vотн (dM / dt ) описывает скорость, с которой импульс
передается системе (или уносится от нее), благодаря добавлению
или выносу из нее массы. Поэтому это слагаемое можно
рассматривать как своего рода силу, которая обусловлена
добавлением (или выбрасыванием) массы и действует на систему
массой М. Для ракеты это слагаемое называют силой реактивной
тяги, т.к. оно описывает силу, возникающую в результате
выбрасывания продуктов сгорания и действующую на ракету.
Уравнение 8.12,б – уравнение движения тела переменной
массы, которое впервые было выведено И.В. Мещерским.
Из уравнения 8.12,б можно получить уравнение Э.К.
Циолковского (при условии что на ракету не действуют
внешние силы):
 m0 
V  U  ln  
m
Оно показывает:
1) чем больше конечная масса ракеты М, тем больше
должна быть стартовая масса ракеты М0;
2) чем больше скорость истечения газов , тем больше
может быть конечная масса при данной стартовой
массе ракеты.
Выражения 8.12 получены для нерелятивистского
случая.
Сегодня: понедельник, 9 мая 2016 г.
Лекция 9
Тема: ДИНАМИКА ВРАЩАТЕЛЬНОГО
ДВИЖЕНИЯ
Содержание лекции:
9.1.Введение
9.2.Момент силы
9.3.Момент импульса
9.4.Закон сохранения момента импульса для
системы частиц
9.5.Вращение вокруг неподвижной оси. Момент
инерции
9.6.Кинетическая энергия вращения
9.7.Гироскоп
9.1. Введение
Для описания вращения полезно ввести новые
физические величины  причину изменения
состояния вращения тела, называемую моментом
силы, и величину, которая изменяется под
действием момента силы,  момент импульса. Эти
величины подобны силе и импульсу в динамике
поступательного движения. Изучать вращение и
вводить такие новые понятия, как момент силы и
импульса, удобно на примере вращения твердого
тела вокруг неподвижной оси, причем каждая точка
твердого
тела
движется
в
плоскости,
перпендикулярной к этой оси,  плоское, двумерное
вращение. Затем легко обобщить полученные
результаты на случай трехмерного вращения.
9.2. Момент силы
Пусть тело вращается в плоскости x y вокруг оси,
перпендикулярной плоскости x y (рис. 9.1).
При повороте на угол  произвольная точка А тела
сместится из положения, задаваемого координатами (x,y), в
точку В, отстоящую от (x,y) на
расстоянии:
y
x   ABsin   r   y,
r
x
y  ABcos  r   x.
r
Причиной изменения состояния
Рис. 9.1
вращения тела служит момент
силы - величина, изменяющая
угловую скорость вращения тела. Момент, по-видимому, от
латинского слова movimentum – способность силы двигать
объект, тем более заметная, чем больше плечо силы.
При плоском повороте тела на угол d под
действием силы F(Fx,Fy) совершается работа,
равная A = (F,dr) = Fxdx + Fydy = (xFy  yFx)d.
В двумерном случае работа пропорциональна
углу d поворота, умноженному на M = xFy – yFx
– величину, получившую название
момента
силы. В случае двух измерений имеем для
момента силы M = xFy – yFx.
Если на тело действует несколько сил, тогда
элементарная работа равна сумме работ,
совершаемой каждой силой:
n
n
nk 1
k 1
A   (Fk , d rk )   ( Fxk dxk  Fyk dyk ) 
n
d  ( xx Fyk  yk Fxk )  ( M k )d  Md
k 1
k 1
этот закон сложения моментов, как скалярных
величин, справедлив лишь для случая плоского
вращения, когда векторы
d = dt
и Mk –
параллельны и направлены перпендикулярно
плоскости xy.
Геометрически условие А = Md означает
следующее. Пусть тело под действием силы F,
приложенной к точке А, поворачивается на угол d. В
этом случае работа по перемещению тела равна
составляющей силы в
Рис. 9.2
направлении перемещения
Ft, умноженной на
перемещение rd (рис. 9.2)
A = rd |F| sin = Ft rd,
Работа равна тангенциальной составляющей силы Ft,
умноженной на перемещение rd. Момент равен
составляющей силы, перпендикулярной радиусу Ft,
умноженной на радиус r - вращать тело вокруг оси может
только составляющая силы, перпендикулярная к радиусу
вращения и эта способность силы изменять состояние
вращения выражена тем сильнее, чем дальше приложена
сила от оси вращения.
A = rsinFd = rFd,
т.е. M = rF, где r = rsin  перпендикуляр, опущенный из
оси вращения на линию действия силы, называемый плечом
силы.
Поскольку внутренние силы направлены по одной прямой,
но в противоположные стороны, а плечо для каждой пары
сил одинаково,  это перпендикуляр, опущенный на линию
действия сил, то сумма моментов всех внутренних сил равна
нулю, и изменить состояние вращения тела могут только
моменты внешних сил.
При вращении тела в плоскости xy относительно
оси z совершаемая элементарная работа равна
A=Md=Mz(k,k)zdt = (Mz,z)dt.
Соответственно, при вращении в плоскости xz и
yz относительно осей y и x, имеем
A=(My,y)dt,
A=(Mx,x)dt.
Элементарная работа при вращении в трех
измерениях равна
A = ((xFy - yFx)k + (zFx – xFz)j + (yFz – zFy)i, ) =
= (M,)dt = (M,d).
Величина момента сил равна
M = (yFz – zFy)i + (zFx – xFz)j + (xFy - yFx)k =
i
j
= x
y
Fy
Fx
k
z  r, F 
Fz
Вектор M перпендикулярен плоскости, в которой
расположены векторы r, F,
причем вращение
вектора r к F на наименьший угол, если его
наблюдать из конца вектора М, происходит против
часовой стрелки (правило правого винта). Для
системы материальных точек
n
M  Mk
k 1
-момент равен сумме моментов от всех внешних
сил, в силу аддитивности работы  полная
элементарная работа равна сумме элементарных
работ, совершаемой каждой из приложенных сил.
Понятие о моментах силы является одним из
основных понятий механики.
9.3. Момент импульса
Подобно тому, как внешняя сила определяет
скорость изменения импульса системы частиц,
так и момент силы определяет скорость
изменения некоторой величины L, называемой
моментом импульса, или угловым моментом
системы частиц. Рассмотрим вначале плоское
вращение одной частицы относительно оси О,
например, по эллипсу, подобно вращению
планеты А вокруг Солнца О. На тело массой m
действует момент силы, где силы равны:
2
d 2x
d
y
Fx  m 2 Fy  m
dt
dt 2
d2y
d 2x
M z  xFy  yFx  xm 2  ym 2
dt
dt


dy
d 
dx  d
  xm  ym  
xp y  yp x .
dt 
dt
dt  dt
Рис. 9.2. Определение
момента импульса L
относительно оси
Оказывается, что момент силы равен скорости
изменения величины Lz = xpy  ypx, называемой
моментом импульса, или угловым моментом.
В случае трех измерений момент импульса
определяется как векторное произведение
L = [r,p],
где p – импульс частицы, r – радиус-вектор,
проведенный из начала системы координат к
частице.
9.4. Закон сохранения момента импульса
для системы частиц
Пусть тело состоит из множества частиц, на
которые действуют внутренние и внешние силы.
Для каждой из частиц имеем (i – intrinsic, M(i) –
моменты внутренних, e – extrinsic, M(e) –
внешних сил):
(i )
(e)
zk
zk
zk
M
M
dL

dt
Просуммировав это выражение по всем частицам
системы, получим
(i )
Mz
.

(e)
Mz
dLz

dt
Поскольку внутренние силы – действие и
противодействие – по третьему закону Ньютона
равны, действуют по одной прямой в
противоположных направлениях и равны их
плечи (перпендикуляр, опущенный от оси
вращения на линию действия сил), то моменты
внутренних сил взаимно сокращаются Mz (i) = 0.
Поэтому скорость изменения момента импульса
системы материальных точек относительно оси
определяется
моментом
внешних
сил
относительно этой же оси:
M
(e)
z
dLz

dt
Полученное соотношение справедливо для
движения любой совокупности частиц.
Независимо от того, образуют они твердое
тело или нет. Если на систему не действуют
внешние силы или сумма этих моментов
равна
нулю,
либо
силы
являются
центральными,
то
момент
количества
движения системы остается постоянным.
Полученные соотношения легко обобщаются
на трехмерный случай.
M = i(yFz – zFy) + j(zFx – xFz) + k(xFy –yFx) =
 d 2z
d 2 y   d 2x
d 2z   d 2 y
d 2x 
 i ym 2  zm 2   j zm 2  xm 2   k  xm 2  ym 2  
dt   dt
dt   dt
dt 
 dt
i
j k
L  x y z  r , p.
Px Py Pz
Здесь L  трехмерный момент импульса
относительно центра вращения О.
Векторная
запись
динамического
закона
вращения в трехмерном пространстве по форме
напоминает уравнение Ньютона F = dp/dt
dL
M=
dt
-Основное уравнение
динамики вращательного движения
Если сложить уравнения вращения для каждой из
частиц системы, то получим, что внешний момент
сил, действующих на систему, равен скорости
изменения полного момента количества движения
системы:
n
dL полн
d n
(e)
(i )
(e)
M   Mk  Mk   Lk 
dt k 1
dt
k 1
Если полный момент внешних сил равен нулю, то
вектор полного момента импульса остается
постоянным – закон сохранения момента
импульса. Закон сохранения момента импульса
есть следствие изотропности пространства –
отсутствия
в
пространстве
выделенных
направлений.


Мы вывели закон сохранения момента
импульса для замкнутой системы. Он
является
прямым
следствием
законов
Ньютона и изотропности пространства –
эквивалентности свойств пространства в
различных
направлениях.
Существует
множество различных задач, связанных с
вращающимися
системами,
в
которых
скорости вращения или моменты импульса
можно вычислить с помощью закона
сохранения момента импульса.
ПРИМЕР: Студент на вращающейся скамье
(скамья Жуковского) держит в вытянутых руках
пару гантелей. Он вращается со скоростью 1
= 0,5 об/с, затем сгибает руки и прижимает
гантели к груди и начинает вращаться с угловой
скоростью 2, которую мы и определим. Будем
считать,
что
первоначально
гантели
находились на расстоянии 60 см от оси
вращения, а после того, как они были прижаты
к груди, – на расстоянии 10 см. Масса гантелей
такова, что моменты импульса студента и
гантелей
в
первоначальном
положении
одинаковы.
Начальный момент импульса гантелей дается
выражением
Ld1 = R1mv1 = R1m(1R1) = m1R12,
где m – масса двух гантелей. Начальный момент
импульса системы равен
L1 = L s1 + m1R12,
здесь L s1 – начальный момент импульса студента.
Поскольку по условию L s1 = L d1, имеем
L s1 = m1R12.
Запишем момент импульса системы, когда гантели
находятся на расстоянии R2:
L2 = L s2 + m2R22.
Применяя закон сохранения импульса системы,
имеем
L s2 + m2R22 = L s1 + m1R12.
Момент импульса студента пропорционален
скорости его вращения, поэтому
L s2 =
2
Ls1 .
1
Подставляя этот результат в предшествующее
равенство, получаем
2
Ls1
+ m2R22 = L s1 + m1R12.
1
Подставим теперь сюда выражение
L s1 = m1R12.
В результате находим
2 =
21
2
R1
2
R1

2
R2
2(0,6) 2
1
 2  (0,5)
с
 0,97 об/с
2
2
(0,6)  (0,1)
Мы видим, что угловая скорость вращения почти
удваивается.
Аналогичный
принцип
работает,
когда
вращающийся на коньках фигурист прижимает к
себе руки и «группируется».
6.5. Вращение твердого тела вокруг
неподвижной оси. Момент инерции
Пусть частицы образуют твердое тело, способное
вращаться вокруг некоторой оси. Любая часть
этого тела расположена неизменным образом
относительно других его частей. Найдем полный
момент импульса относительно неподвижной оси.
Пусть масса k-й частицы равна mk, и она
расположена на расстоянии rk от оси.
Рис. Вращающийся
диск(показан элемент
массы mk),
удаленный на расстояние
rk от оси вращения
Момент импульса k-й частицы равен
Lk = mkvkrk.
Угловая скорость вращения тела  связана с
линейной скоростью точки соотношением vk = rk,
и, следовательно,
Lk = mkvkrk = Lk = mkrk2.
Полный момент количества движения тела равен
сумме моментов количества движения всех частиц,
n
n
2
образующих тело:
L   Lk   ωmk rk
k 1
k 1
Вынося одинаковую для всех частиц системы
угловую скорость за знак суммы и вводя
n
обозначение
I
k 1
2
m k rk , получаем
L = I.
Это выражение похоже на формулу для
импульса р= mv в динамике поступательного
движения. Скорость заменяется на угловую
скорость, а масса на некую величину I,
называемую моментом инерции. Момент
инерции играет роль массы при вращении и
служит мерой инерции во вращательном
движении. Величина I зависит не только от
массы тела, но и от того, как масса
распределена относительно оси вращения.
Тело
обладает
моментом
инерции
независимо от того, вращается оно или нет.
Между массой и моментом инерции
имеется существенная разница – масса
тела обычно не изменяется, тогда как
момент
инерции
можно
изменить
перемещением масс относительно оси
вращения. Пусть мы находимся на
подставке, способной вращаться вокруг
неподвижной оси (скамья Жуковского), и
вращаемся с разведенными руками. Можно
уменьшить начальный момент инерции
тела I1, опустив руки. При этом масса всей
системы не изменится, но момент инерции
уменьшится до I2.
Если момент внешних сил равен нулю, то в
силу закона сохранения момента импульса
имеем:
I11 = I22 = L = const,
откуда следует, что угловая скорость вращения
увеличится
I1
2 = 1
> 1.
Как
уже
отмечалось, I 2 этим, например,
пользуются
фигуристы
для
увеличения
скорости
своего
вращения.
Уравнение,
описывающее
вращение
тела
вокруг
неподвижной оси, принимает вид
dL d I
М  
dt
dt
Если
момент
инерции
тела
остается
неизменным, то основное уравнение динамики
вращательного движения переходит в следующее:
d
M = I,  =
dt
,
что напоминает по форме второй закон Ньютона,
где роль силы играет момент силы, линейное
ускорение заменено на угловое, а мерой
инертности тела служит момент инерции.
Физический же смысл этого уравнения и входящих
в него величин принципиально отличен от второго
закона Ньютона, хотя оно и есть прямое его
следствие.
6.8. Расчет моментов инерции
Момент инерции тела относительно оси можно
рассчитать или измерить. По определению имеем:
n
I   mi ri .
2
k 1
Если вещество распределено в теле непрерывно,
то, разбив тело на бесконечно малые элементы
dmi(r), получим
2
I   r dm( r ).
V
Интегрирование выполняется по всему объему,
занимаемому телом.
Пусть произвольные оси вращения тела проходят
через точки О и А, перпендикулярно плоскости
вращения (рис. 6.17).
Моменты инерции относительно
осей О и А равны:
2

I 0   r dm, I A   r  dm
2
.Поскольку r + a = r,
(r’)2 = r2 + a2 – 2(r,a),


то имеем:

I A  r 2 dm  a 2 dm  ( 2a, rdm) 
= I0 + a2M – 2(a,MRС).
Здесь R  M 1 r dm  радиус-вектор центра
C

масс тела относительно оси О.
Если ось O проходит через центр масс тела, то RC =
0 и полученное соотношение упрощается:
IA = IC + a 2M
– момент инерции тела относительно произвольной
оси А равен моменту инерции его относительно оси
C, проходящей через центр масс, плюс произведение
Ma2, где M – масса тела, a – расстояние между
данными параллельными осями. То есть момент
стержня относительно оси (АА) равен моменту
инерции
стержня
относительно
оси
(ОО),
проходящей через центр масс, плюс произведение
массы стержня на квадрат расстояния между осями.
Это
утверждение
называется
теоремой
о
параллельном переносе оси или теоремой Штейнера
(Якоб Штейнер, швейцарский геометр, 1796  1863).
Моменты инерции некоторых распространенных тел
(относительно указанных на рисунках осей)
2
ml
12
МR2
кольцо

1
m R 2  r12
2
Стержень-центр

Кольцо толщиной R-r1
3
2
mR
2
Диск(край)
ml
3
2
Стержень-край
2
mR 2
5
шар
2
mR 2
3
Сферическая оболочка
6.6. Кинетическая энергия вращения
Пусть тело вращается вокруг некоторой оси, так
что каждая его точка движется со скоростью rk,
где rk – расстояние от данной точки до оси. Если
масса точки равна mk, то полная кинетическая
энергия тела равна сумме кинетической энергии
n
1 n
1
2
его частиц:
2
K
 mk v k   mk rk  .
2 k 1
2 k 1
Поскольку угловая скорость постоянна для всех
1 2 n
1 2
точек, то имеем
2
K
2
  mk rk 
k 1
2
 I.
Можно записать выражение для кинетической
энергии и в другом виде. Поскольку L = I , то
имеем
L2
K=
2I
Эти выражения подобны соответствующим
выражениям
для
кинетической
энергии
поступательного движения точки при формальной
замене: m → I, v → , P → L. Воспользовавшись
теоремой Штейнера, можно переписать выражение
для кинетической энергии в виде


1
1 2
2
1 2
2
m
v

I
K =  I C  ma =
C +
2
2
2
Кинетическая энергия представляет собой сумму
кинетических энергий вращения тела относительно
оси, проходящей через центр масс, плюс
кинетическая энергия поступательного движения
центра масс.
Скорость центра масс обруча равна v, масса обруча
m. Определим его кинетическую энергию при
движении по горизонтальной поверхности.
Имеем
1
1
2
2 ,
Kполн =
mv + mvобод
2
2

v обод
– линейная скорость обода
в системе ц.м. Для наблюдателя,
движущегося вместе с центром
обруча, скорость точки
соприкосновения обруча с плоскостью

равна v. Поэтому v обод
= v.
1
1
2
2
m
v
m
v
Таким образом, Kполн =
+
= mv2.
2
2
Следует заметить, что энергия катящегося
обруча вдвое превышает энергию тела с той
же массой m, движущегося с той же скоростью,
но без вращения, т.е. только поступательно.
Рассмотрим автомобиль с маховиком вместо
двигателя. Во время стоянки автомобиля
маховик мог бы накапливать энергию с
помощью небольшого высокоэффективного
электромотора. Автомобиль, использующий
энергию маховика, мог бы пробежать примерно
1/3 расстояния, которое пробегает обычный
автомобиль с запасом бензина
40 л (около 100 км).
6.7. Гироскоп
Гироскоп – быстро вращающееся симметричное
твердое тело, ось вращения которого может
изменять свое направление в пространстве.
Название «гироскоп» происходит от греческого
gyréuō – кружусь, вращаюсь, и skopéō – смотрю,
наблюдаю.
Гироскоп обладает интересными
свойствами, проявляющимися у вращающихся
небесных тел, артиллерийских снарядов, роторов
турбин, установленных на судах. На свойствах
гироскопов основаны различные приборы и
устройства, применяемые в современной технике.
Свойства
гироскопов
реализуются
при
выполнении двух условий:
1.Ось вращения гироскопа должна иметь
возможность изменять свое положение в
пространстве;
2.Угловая скорость вращения гироскопа
вокруг своей оси должна быть очень велика
по сравнению со скоростью изменения
направления оси в пространстве.
Чтобы ось гироскопа могла свободно
поворачиваться в пространстве, его обычно
закрепляют на кольцах т.н. карданова
подвеса
Пусть
симметричное
тело
вращается с большой угловой
скоростью  вокруг оси y, и к оси
гироскопа приложена пара сил F,
перпендикулярная
оси
y
и
лежащая в плоскости xy (рис.
6.24).
При
этом
возникает
момент M, перпендикулярный
вращательный
плоскости xy.
Поскольку dL = Mdt  изменение момента
количества движения направлено параллельно
вектору M, то ось гироскопа повернется вокруг оси х
в направлении, перпендикулярном действию силы.
Используя равенства dL = Ld и dL = Mdt,
получаем M = L0 = L0.
Учитывая направления векторов, имеем
M = [,L0].
Это уравнение позволяет определить момент
силы, который необходимо приложить, чтобы
заставить гироскоп вращаться с угловой
скоростью  . Величина  носит название
угловой скорости прецессии, т.е. скорости
вращения гироскопа относительно оси x.
Если к оси гироскопа приложена сила с
моментом М, то угловая скорость прецессии
равна
M
M

=
,
Lsin  Isin 
где α  угол между направлениями вектора
силы F и вектором L0, I – момент инерции
гироскопа относительно оси y,   угловая
скорость собственного вращения гироскопа
вокруг оси y, M – момент силы F относительно
центра О.
Из формулы следует, что скорость прецессии 
тем медленнее, чем больше величина I,
называемая
собственным
кинетическим
моментом гироскопа или моментом количества
движения.
Прецессия гироскопа возможна лишь при
действии момента сил на ось гироскопа (M ≠ 0)
Вращение прекратится, как только исчезнет
силовое воздействие на ось гироскопа М = 0.
Этим гироскоп принципиально отличается от
невращающегося тела. Невращающееся тело
под влиянием приложенного момента начинает
ускоренно вращаться, и это вращение будет
происходить
с
достигнутой
скоростью
бесконечно долго и после прекращения
действия момента – закон сохранения момента
импульса. Гироскоп начинает вращаться с
постоянной угловой скоростью Ω сразу после
приложения
момента
силы
M
и
останавливается
немедленно
после
прекращения действия момента силы.
Пример
прецессионного
вращения
дает
артиллерийский снаряд. Если снаряд не вращается
вокруг собственной оси, то под действием силы
сопротивления воздуха он начинает кувыркаться. Его
полет становится беспорядочным, при этом
значительно возрастает сопротивление движению и
уменьшается дальность полета. Вращающийся
вокруг оси снаряд обладает всеми свойствами
гироскопа, и сила сопротивления воздуха вызывает
его прецессию вокруг прямой, по которой направлена
его скорость, т.е. вокруг касательной к траектории
движения центра тяжести. Это делает полет
правильным и обеспечивает попадание в цель
головной частью. Вращение снаряду придают
специальные направляющие в стволе орудия 
нарезные стволы.
Если гироскоп находится в кардановом
подвесе, то он имеет три степени свободы.
Гироскоп на кардановом подвесе не
испытывает действия момента в результате
вращения Земли или в результате движения
самолета, в котором он находится. Поэтому
ось вращающегося тела будет сохранять
определенное направление в пространстве.
Если эту ось направить на звезду, то при
любых перемещениях прибора и толчках она
будет продолжать указывать на эту звезду,
меняя свою ориентировку относительно осей,
связанных с Землей.
Если ось ротора закреплена в основании и это
основание неподвижно, то ось гироскопа не может
изменять свое направление в пространстве. Если
вращать основание с угловой скоростью Ω, то ось
ротора будет давить на подшипники с моментом
силы
M = Isin.
На морских судах и самолетах имеется много
вращающихся частей: вал двигателя, ротор
турбины, гребные и воздушные винты и т.д. При
разворотах судна, качке на подшипники, в которых
укреплены эти вращающиеся части, действуют
указанные гироскопические силы, и их необходимо
учитывать при соответствующих инженерных
расчетах, чтобы избежать катастрофы.
4. ЗАКОНЫ СОХРАНЕНИЯ И ИХ
СВЯЗЬ С СИММЕТРИЕЙ
ПРОСТРАНСТВА-ВРЕМЕНИ
В предыдущих лекциях нами были рассмотрены три
основных закона природы: законы сохранения импульса, момента
импульса и энергии. Следует понимать, что эти законы
выполняются только в инерциальных системах отсчета. В самом
деле, при выводе этих законов мы пользовались вторым и третьем
законами Ньютона, а последние применимы только в инерциальных
системах.
Напомним также, что импульс и момент импульса
сохраняются в том случае, если систему можно считать замкнутой
(сумма всех внешних сил и собственно всех моментов сил равна
нулю). Для сохранения же энергии тела условия замкнутости
недостаточно – тело должно быть еще и адиабатически
изолированным (т.е. не участвовать в теплообмене).
Во всей истории развития физики, законы сохранения
оказались чуть ли не единственными законами,
сохранившими свое значение при замене одних теорий
другими. Эти законы тесно связаны с основными
свойствами пространства и времени.
1. В основе закона сохранения энергии лежит
однородность времени, т.е. равнозначность всех моментов
времени. Равнозначность следует понимать в том смысле,
что замена момента времени t1 на момент времени t2 без
изменения значений координат и скорости частиц не
изменяет механические свойства системы. Это означает
то, что после указанной замены координаты и скорости
частиц имеют в любой момент времени t2+t такие же
значения, какие они имели до замены в момент времени
t1+t.
2. В основе сохранения импульса лежит однородность
пространства, т.е. одинаковость свойств пространства во
всех точках. Одинаковость следует понимать в том
смысле, что параллельный перенос замкнутой системы из
одного места пространства в другое без изменения
взаимного расположения и скоростей частиц не изменяет
механические свойства системы (предполагается, что на
новом месте замкнутость системы не нарушается).
3. В основе сохранения момента импульса лежит
изотропия пространства, т.е. одинаковость свойств
пространства по всем направлениям. Одинаковость
следует понимать в том смысле, что поворот замкнутой
системы как целого не отражается на ее механических
свойствах.
Между законами типа основного уравнения динамики и
законами сохранения имеется принципиальная разница.
Законы динамики дают нам представление о детальном
ходе процесса. Так, если задана сила, действующая на
материальную точку, и начальные условия, то можно
найти закон движения, траекторию, величину и
направление скорости в любой момент времени и т.п.
Законы же сохранения не дают нам прямых указаний на
то, как должен идти тот или иной процесс. Они говорят
лишь о том, какие процессы запрещены и потому в
природе не происходят.
Таким образом, законы сохранения проявляются как
принципы запрета: любое явление, при котором не
выполняется хотя бы один из законов сохранения,
запрещено, и в природе такие явления никогда не
Всякое явление, при котором не нарушается ни один из
законов сохранения, в принципе может происходить.
Рассмотрим следующий пример. Может ли
покоящееся тело за счет своей внутренней энергии начать
двигаться? Этот процесс не противоречит закону
сохранения энергии. Нужно лишь, чтобы возникшая
кинетическая энергия точно равнялась убыли внутренней
энергии.
На самом деле такой процесс никогда не
происходит, ибо он противоречит закону сохранения
импульса. Раз тело покоилось, то его импульс был равен
нулю. А если оно станет двигаться, то его импульс сам
собой увеличится, что невозможно. Поэтому внутренняя
энергия тела не может превратиться в кинетическую, если
тело не распадется на части.
Если же допустить возможность распада этого тела на
части, то запрет, налагаемый законом сохранения
импульса, снимается. При этом возникшие осколки могут
двигаться так, чтобы их центр масс оставался в покое, - а
только этого и требует закон сохранения импульса.
Итак, для того чтобы внутренняя энергия
покоящегося тела могла превратится в кинетическую, это
тело должно быть способно распадаться на части. Если же
есть еще один какой- либо закон, запрещающий распад
этого тела на части, то его внутренняя энергия и масса
покоя будут постоянными величинами.
Подчеркнем, что законы сохранения энергии, импульса и
момента импульса являются точными законами, строго
выполняющимися и в релятивистской области.
ЛЕКЦИЯ ОКОНЧЕНА
УРА! УРА! УРА!
ДО СВИДАНИЯ!