1.Обратные тригонометрические функции.
реклама
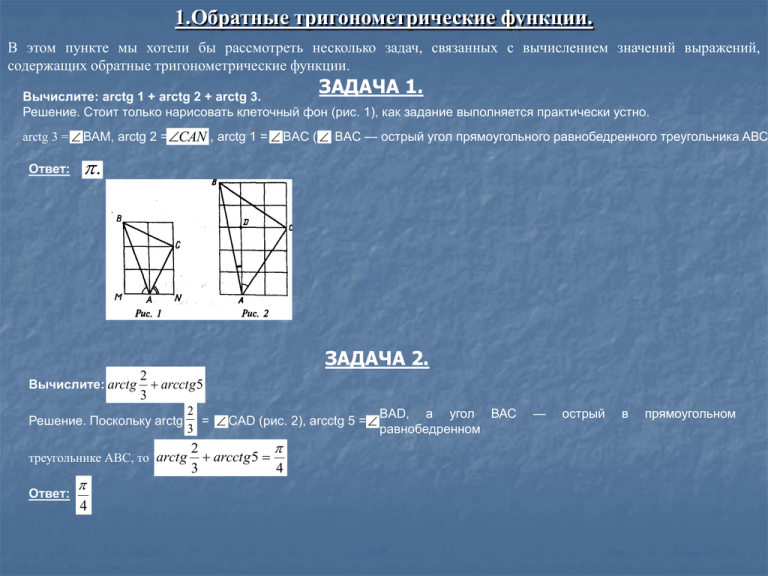
1.Обратные тригонометрические функции. В этом пункте мы хотели бы рассмотреть несколько задач, связанных с вычислением значений выражений, содержащих обратные тригонометрические функции. ЗАДАЧА 1. Вычислите: arctg 1 + arctg 2 + arctg 3. Решение. Стоит только нарисовать клеточный фон (рис. 1), как задание выполняется практически устно. arctg 3 = ВАМ, arctg 2 =CAN , arctg 1 = BAC ( BAC — острый угол прямоугольного равнобедренного треугольника AВС Ответ: . ЗАДАЧА 2. Вычислите: arctg 2 arcctg 5 3 Решение. Поскольку arctg 2 BAD, а угол ВАС = CAD (рис. 2), arcctg 5 = 3 равнобедренном треугольнике АВС, то arctg 2 arcctg 5 3 4 Ответ: 4 — острый в прямоугольном ЗАДАЧА 3. Вычислите: ctg ( 1 arccos 5 ) 2 13 Решение. Если использовать понятия косинуса и котангенса острого угла прямоугольного треугольника, теорему Пифагора и свойство биссектрисы треугольника, то задача решается почти мгновенно. На рис. 3 изображен треугольник АВС,, в котором ACB = 90°, ВС = 5, АВ = 13 и ВМ - биссектриса угла АВС. Следовательно, 2 МС = 5х, АМ= 13х и АС= 12, отсюдаx . Тогда 3 40 Вычислите sin( 2 arccos ) 41 ЗАДАЧА 4. Решение. Рассмотрим равнобедренный треугольник АBС, где АB=BС=41, ВМ АС, ВМ=40,CN AB (рис.4). Отрезок AM согласно теореме Пифагора имеет длину, равную 9. Видно, что sin( 2 arccos CN AC BM 720 . AB 41 40 CN ) . Воспользовавшись подобием прямоугольных треугольников ANC и AMB, найдем 41 BC 2. Алгебраические выражения. Часто в алгебре встречаются задания, в которых по заданным условиям на переменные, необходимо найти значение некоторого выражения, содержащего их. ЗАДАЧА 5. Из условий выражения x2 y2 9 x y y z. , y 2 z 2 16 и y 2 x z для положительных х, у и z, не вычисляя их значений, указать значение Решение. Привычное задание решить систему уравнений у учащихся затруднений не вызывает. Однако в данном случае нужно, не решая систему, ответить на вопрос, чему равно значение выражения ху + yz. По теореме, обратной теореме Пифагора, числа х, у и z являются соответственно длинами катетов и гипотенузы треугольника ABD с прямым углом D. А, рассмотрев второе уравнение системы, можно сделать вывод, что у, z и 4 также есть соответственно длины катетов и гипотенузы треугольника BCD с прямым углом D (рис. 6). Третье уравнение системы разрешает утверждать, что число у есть среднее пропорциональное чисел х и z, и по теореме, обратной теореме о пропорциональных отрезках в прямоугольном треугольнике, угол АВС — прямой. Теперь рассмотрим выражение ху + yz. xy yz ( x z ) y 2S ABC 3 4 12 Примечание. Для данной системы уравнений задания могут быть и другие. Например, найти значение выражения х + у + z или в каком отношении находятся числа х и у; z и у; х + z и у. Ответ: 12 Задача 6. Для положительных х, у и z из условий x 2 xy вычислите значение выражения ху + уz + zx. y2 z2 2 2 2 169, y z 50, x xz 144, не находя значения х, у и z, 2 2 Решение. Запишем три условия задачи в виде системы уравнений x z По теореме, обратной теореме, Пифагора, числа, и 5 являются длинами соответственно катетов и гипотенузы 2 2 треугольника АОС с прямым углом АОС. y. Числа х, и 13 есть длины сторон треугольника АОВ с углом АОВ, равным 135°. Этот вывод можно сделать, используя 2 z теорему, обратную теореме косинусов. Аналогично, 2x, и 12 есть длины сторон треугольника ВОС с углом ВОС, равным 135°. Поскольку 52 + 122 = 132, то в треугольнике ACB = 90°. Теперь найдем площади На рис. 8 изображены эти треугольники. АВС треугольников АОВ, АОС, ВОС, АВС. Видно, что значение выражения ху + yz +zx равно учетверенной площади треугольника ABC. Итак, xy+yz+zx =120 Ответ:120 ЗАДАЧА 7. Для положительных х, у и z, не вычисляя их значения из системы уравнений определите величину ху + 2уz + Зxz. Рассуждая так же, как и в задаче 8, получаем (рис. 9): Так как площадь треугольника AВС равна 6, то xy 2 yz 3 xz 24 3. Ответ: 24 3 3. Системы уравнений. Решению систем уравнений в алгебре отводится достаточно большое внимание. Они встречаются и в вариантах ЕГЭ. Поэтому, тем более, интересен такой нестандартный подход к решению некоторых систем уравнений, рассмотренных в этом пункте. ЗАДАЧА 8. Имеет ли система уравнений решения для х > 0, у > 0 и z> 0? Допустим, что есть такая тройка положительных чисел х, у и z, удовлетворяющая каждому уравнению данной системы. Тогда возможна ее геометрическая интерпретация, как в задаче 8 (рис.10). Но такого треугольника АВС не может быть, так как не выполняется неравенство треугольника. Значит, система не имеет решений. Примечание. Для положительных x,y и z данная система имеет решение, если в правой части третьего уравнения поставить число из промежутка (1; 25). Ответ: нет решений. рис.10 ЗАДАЧА 9. Решите систему уравнений Решение. Нетрудно убедиться, что х и у положительны. Поскольку y 2 ( x 2 y 2 ) 2 x 2 , то числа у, x 2 y 2 и х являются длинами соответственно катетов и гипотенузы треугольника АВС с прямым углом АСВ (рис. 11). Площадь этого треугольника 24 кв. ед., а его периметр 24 ед. Поэтому радиус окружности, вписанной в треугольник АВС, равен 2. Так как длина гипотенузы АВ равна сумме длин катетов АС и ВС без удвоенной длины радиуса вписанной в треугольник окружности, то Из второго уравнения системы получаем х = 10. Значит, у = 6 или у = 8. Ответ: (10; 6), (10; 8). ЗАДАЧА 10. Решите систему уравнений Решение. Первое уравнение системы задает плоскость, второе — сферу. Если их изобразить, то очевидно, что 0<х<1, 0 < у < 1, 0<z<1. Согласно первому уравнениюz 3 ( x y ). z 1 3 Тогда второе уравнение принимает вид (*) Преобразовав его, получаем квадратное уравнение относительно х: y 3 -1)2. Следовательно, -(у3 -1)2 0. Этонеравенство выполняется при Дискриминант этого уравнения равен - (у 1 3 1 у Уравнение (*) можно было преобразовать в квадратное относительно у с решением 3 1 Значение z находится из первого уравнения. 3 Примечание. Задачу можно переформулировать, например, так: «Определите вид треугольника, периметр которого равен а сумма квадратов длин его сторон равна 1». 3 , ЗАДАЧА 11. Решите систему уравнений Решение. Уравнение x+y+z=3 - есть уравнение плоскости (рис. 12), пересекающей оси прямоугольной декартовой системы координат в , А(3;0;0), B(0;3;0), С(0; 0; 3). Уравнение x 2 y2 z2 3 3 есть уравнение сферы с центром в точке O(0; 0; 0) и радиусом равным R, 1 Вычислим расстояние от точки О до плоскости AВС. Для этого рассмотрим тетраэдр ОАВС. Объем V тетраэдра равенS ABC H 3 где H=OD (D — центр треугольника АВС). Этот объем можно найти иначе: 3H 3 и 9 , получаем H= 3 . Это означает, что расстояние от точки О до плоскости АВС равно радиусу сферы, а значит, 2 2 плоскость касается сферы. Следовательно, точка касания является центром треугольника АВС. Поскольку D(x; у; z) — центр Приравняв равностороннего треугольника АВС, где А(3; 0; 0), В(0; 3; 0), С(0;0;3), то x=y=z. Заменив у и z на х в уравнениях данной системы, получаем x=1. Ответ: (1; 1; 1). ЗАДАЧА 12. Решите систему уравнений Решение. Рассмотрим слагаемые левой части второго уравнения: x 2 y 2 4 x 2 y 5 ( x 2) 2 ( y 1) 2 Пусть это расстояние между точками М(х; у) и A(2;-1). Допустим, что это расстояние между точками М (х;у} и В(10; 5). Найдем расстояние между точками А(2; -1) и В(10;5): AB (10 2) 2 (5 1) 2 10 Итак, второе уравнение системы можно интерпретировать как равенство AM + ВМ = АВ. Это дает нам право утверждать, что точка М принадлежит отрезку АВ, т.е. 2 ≤ х ≤ 10 и -1 ≤ у ≤ 5 Составим уравнение прямой АВ, проходящей через точки А(2; -1) и B(10; 5). 1 k 2 b и 5 k 10 b. Отсюда k 3 ; b 5 , т.е. y 3 x 5 , или Зх — 4у = 10. Запишем новую 4 2 4 2 систему: Значит, х = 6 и у = 2. Ответ: (6; 2). 4. Аналитический способ решения. Рассмотрим аналитический способ решения некоторых задач, рассмотренных выше, чтобы была возможность убедиться в том, что геометрический подход дает более быстрое, а главное, красивое решение этих задач. ЗАДАЧА 1. Рассмотрим аналитический способ решения. Решение. 3 . Обозначим: arctg1, arctg 2, arctg 3, где 2 2 tg tg 23 1 tg tg ( ) 1 tg ( ) 1 tgtg 1 2 3 11 0 Найдем tg ( ) tg tg 23 1 tg tg ( ) 1 tg ( ) 11 1 1 1 tgtg 1 2 3 1 3 2 2 Таким образом, tg ( ) 0 k , учитывая условие, что ( ; ), получим, что k=1 и , т.е. arctg1 arctg 2 arctg 3 . Ответ: ЗАДАЧА 2. Решим систему аналитически: Решение: Обозначим уравнение3 x 4 y 26 - (1), уравнение x 2 y 2 4 x 2 y 5 x 2 y 2 20 x 10 y 125 10 - (2). Заметим, что x 2 y 2 4 x 2 y 5 ( x 2) 2 ( y 1) 2 , а x 2 y 2 20 x 10 y 125 ( x 10) 2 ( y 5) 2 . Сделаем замену x 2 a, y 1 b, тогда уравнение (2) системы запишется в виде: a 2 b 2 (a 8) 2 (b 6) 2 10, a 2 b 2 10 (a 8) 2 (b 6) 2 . Возведем обе части уравнения в квадрат, получим: a 2 b 2 100 (a 8) 2 (b 6) 2 20 (a 8) 2 (b 6) 2 , 20 (a 8) 2 (b 6) 2 100 (a 8) 2 (b 6) 2 a 2 b 2 20 (a 8) 2 (b 6) 2 200 16a 12b 5 (a 8) 2 (b 6) 2 50 4a 3b 25(( a 8) 2 (b 6) 2 ) 2500 16a 2 9b 2 400a 300b 24ab 25a 2 400a 1600 25b 2 300b 900 2500 16a 2 9b 2 400a 300b 24ab (3a 4b) 2 0 3a 4b 3( x 2) 4( y 1) 3 x 4 y 10 Сделаем обратную замену: Получим систему: 3x 4 y 26 x 6 , 3x 4 y 10 y 2 Поскольку мы не следили за равносильностью переходов, сделаем проверку: (1) - 3 6 4 2 26 18 8 26 Ответ: (6;2). (2) - 36 4 24 4 5 36 4 120 20 125 10 5 5 10









