Presentation_28012016
реклама

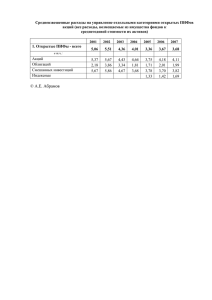
Анализ и прогнозирование разностно-стационарных рядов динамики к.э.н., доцент Ичкитидзе Ю.Р. Модели ряда динамики 1. Тренд-стационарные модели (trend-stationary, TS models) Y Yˆ S Тренд (Yˆ ) выявляется с помощью аналитической функции Устраняется сезонность ( S ) Ряд остатков ( ) должен иметь автокорреляцию существенно ниже 1 Если автокорреляция остатков близка к 1 (выше 0,9) - остатки нестационарные, то есть в будущем тренд сместится (полученная оценка параметров тренда имеет смещение). В этом случае, используют разностно-стационарные модели. 2. Разностно-стационарные модели (difference-stationary, DS models) Вычисляются логарифмические первые разности (first difference) Yt ln( Yt / Yt 1 ) Yt Если стационарен (автокорреляция значительно меньше 1), то строят модель на первых разностях, если нет, то переходят ко вторым разностям 2Yt 2Yt Yt Yt 1 и проверяют их на стационарность. При необходимости, шаги повторяются (третьи, четвёртые разности, и так далее…) Построение модели первых на разностях Если логарифмические первые разности (first difference) Y стационарны, то t модель на первых разностях выглядит следующим образом. Yt 1 Yt r (прогноз первых разностей есть предыдущая разность умножить на коэффициент автокорреляции плюс случайная величина “кси”) N ( , ) (случайная величина “кси” имеет нормальное распределение с параметрами - среднее, - среднеквадратическое отклонение) оценка параметров происходит по ретроспективному ряду Yt Yt 1 r Yt 1 Yt e Yt 1 (имитационный прогноз ряда есть предыдущий элемент ряда умножить на экспоненту в степени прогноз первых разностей) Имитационное моделирование Имитационное моделирование используется для оценки параметров (и вида) распределения случайной величины, если параметры (и вид) её распределения невозможно вычислить аналитически. Для этого: 1. Строится модель имитации (например, имитационный прогноз с предыдущего слайда.) 2. Проводится значительное число имитаций (например, 1000) 3. По полученным исходам имитаций делается оценка параметров (и вида) распределения случайной величины Имитационное моделирование легко можно выполнить в Excel с помощью элементарных макросов (см. файл p5_imit.xlsm). Итоги можно посмотреть в файле p5_itog.xlsm. Корректировка на инфляцию Перед тем, как анализировать экономические показатели, рекомендуется сделать их корректировку на инфляцию. Yt н - номинальный показатель (в текущих ценах) Yt р Pt - реальный показатель (в постоянных ценах, ценах базисного периода, например, в ценах последнего периода) - уровень цен на конец t-ого периода t Pt P0 I k Pt Pt 1 I t Ik k 1 - уровень инфляции (темп роста цен) в k-ом периоде (ед. за период) Pб Yt Yt Pt p Pt н - уровень цен в выбранном базовом периоде Прогноз номинального показателя С помощью моделей рядов динамики (TS или DS) рекомендуется прогнозировать реальные показатели ( Yt р ). В таком случае прогноз номинального показателя (Yt н ) происходит с помощью формулы Yt н Yt р Pt Pб Pt Pt Iˆk k 1 Iˆk - прогноз уровня инфляции (темп роста цен) в k-ом периоде (ед. за период) Прогноз номинального показателя С помощью моделей рядов динамики (TS или DS) рекомендуется прогнозировать реальные показатели ( Yt р ). В таком случае прогноз номинального показателя (Yt н ) происходит с помощью формулы Yt н Yt р Pt Pб Pt Pt Iˆk k 1 Iˆk - прогноз уровня инфляции (темп роста цен) в k-ом периоде (ед. за период) Прогнозирование рыночных цен биржевых инструментов (акций, валют, товаров) finance.yahoo.com Наименование компании finance.yahoo.com / Historical Prices Последняя цена за период Цена, скорректированная (динамика цены без учета выплаченных дивидендов) на выплаченные дивидендов Динамика цен акций IBM c декабря 2005 по декабрь 2015 213.3 129.43 82.20 81.6 Oct 31 ‘08 Mar 1 ‘13 Модель случайного блуждания цен акций (Random walk model)* Pt – ряд динамики цен акций (t-время) yt Pt 1 – доходность акций (без учёта выплаченных дивидендов**) Pt 1 t ln( 1 y ) ln( Pt P ) – непрерывно начисляемая доходность акций t 1 Эмпирические исследования (Osborne, 1954; Fama, 1965) показали, что t имеет распределение, близкое к нормальному, т.е. можно принять что t N ( , ) . Эксцесс (kurtosis) *модель случайного Асимметрия (skewness) Толстые хвосты (fat tails) блуждания это частный случай разностностационарных моделей с r =0 **с учётом дивидендов Pt должно быть скорректировано (adjusted price) Модель случайного блуждания цен акций (Random walk model) t ln( Pt P ) t 1 t Pt Pt 2 e e t 1 Pt Pt 1e t t Pt 2 e По свойствам нормального распределения знаем, что t i 1 i i t t 1 N ( t , t ) Pt P0e i1 4000 3500 3000 Сводный индекс ММВБ Оптимистический сценарий Пессимистический сценарий Случайный исход (имитация) 2500 2000 1500 1000 Pt P0e N ( t , t ) 500 0 сен.97 сен.00 сен.03 сен.06 сен.09 сен.12 Вычисление прогнозных траекторий цены акции с уровнем значимости Оптимистический сценарий (верхняя граница траектории): Pt P0e Нормобр(1 ; t ; t ) P0e t k t Средний сценарий (наиболее вероятная траектория): Pt P0e Нормобр( 0,5; t ; t) P0e t Пессимистический сценарий (нижняя граница траектории): Pt P0e Нормобр( ; t ; t ) P0e t k t 0,25 0,1 0,05 0,01 k 0,674 1,28 1,645 2,32 Спасибо за внимание Контакт: Юрий Ичкитидзе ichkitidze@reflexivity.ru