Доклад на Коллегию

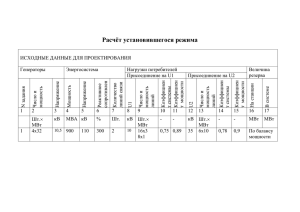
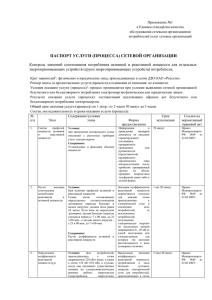
«Научно-исследовательский, проектно-конструкторский и
изыскательский институт»
ФААЭ ФГУП «Атомэнергопроект»
Москва, Российская Федерация
Математическая модель и оценка
динамических усилий, возникающих
при разрывах трубопроводов с
высокоэнергетическим
теплоносителем
Доклад
Плаксеев А.А.
Чуричев А.С.
2008 год
Система дифференциальных уравнений



2
Закон сохранения
массы
Закон сохранения
импульса
Закон сохранения
энергии
Уравнение состояния, начальные и
граничные условия
3

Уравнение состояния

Начальные условия

Граничные условия
Р(z,0)=P0
(z,0)=0
G(z,0)=0
Р(0,)=Pа
G(L, )=0
Уравнения движения жидкости в трубе
переменного сечения
4
Реактивная сила


5
Реактивная сила
действующая на
трубопровод при
истечении
теплоносителя
Коэффициент
реактивной силы
Коэффициент реактивной силы при истечении
насыщенной воды при мгновенном разрыве
трубопровода
Qz
2
1.6
1.2
Qz
0.8
Qw
0.4
QP
0
0
6
0.005
0.01
0.015
0.02
0.025
, c
Скорость звука в двухфазной среде в
зависимости от объемного паросодержания
a, м/с
1400
1200
1000
800
2 МПа
9 МПа
17 МПа
600
400
200
0
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1

Коэффициент реактивной силы при истечении
насыщенной воды с учетом постепенного раскрытия
сечения разрыва (=0,3 мс ).
Qz
1.6
Qz
1.2
Qw
0.8
QP
0.4
0
0
8
0.001
0.002
0.003
,c
Сравнение коэффициента реактивной силы,
рассчитанного по программе ПРУД с данными,
приведенными в ANSI/ANS-58.2-1986.
Qz
1.6
1.2
0.8
0.4
0
0
9
0.001
0.002
0.003
,c
Коэффициент реактивной силы при истечении
насыщенного пара
Qz
1- Qz =1,26
1,3
2 - Qz =1,24
3 - Qz =1,233 (по
1,28
газодинамическим
формулам при k =1,135)
1
1,26
4 - Qz =1,26-Pa/P0
4
5
(ANSI/ANS-58.2-1986)
2
3
1,24
5 – По ПС ПРУД
1,22
1,2
0
4
8
12
16
20
Р, МПа