Задача коммивояжера
реклама
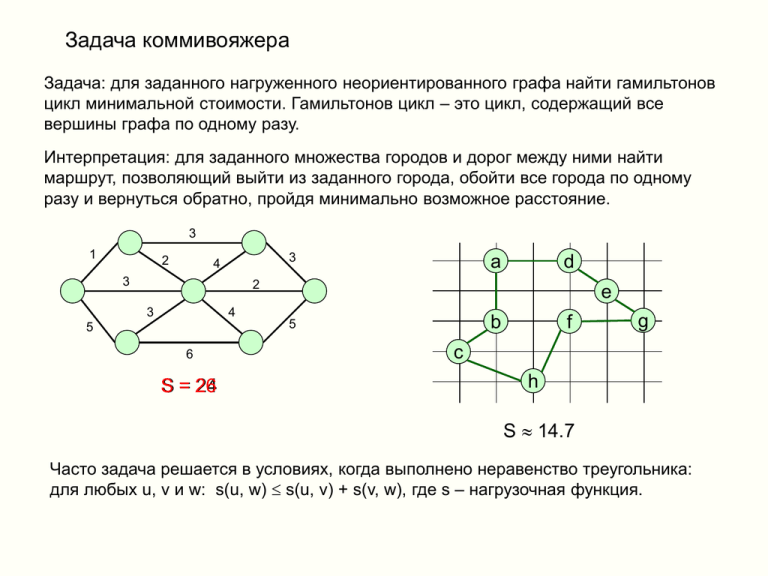
Задача коммивояжера Задача: для заданного нагруженного неориентированного графа найти гамильтонов цикл минимальной стоимости. Гамильтонов цикл – это цикл, содержащий все вершины графа по одному разу. Интерпретация: для заданного множества городов и дорог между ними найти маршрут, позволяющий выйти из заданного города, обойти все города по одному разу и вернуться обратно, пройдя минимально возможное расстояние. 3 1 2 3 4 3 a d 2 3 e 4 b 5 5 6 S = 26 24 f g c h S 14.7 Часто задача решается в условиях, когда выполнено неравенство треугольника: для любых u, v и w: s(u, w) s(u, v) + s(v, w), где s – нагрузочная функция. Алгоритмы решения задачи коммивояжера 1. Возможен простой, но очень неэффективный переборный алгоритм: найти все гамильтоновы циклы, выбрав из них наименьший по стоимости. 2. Возможен «жадный» алгоритм, дающий результат не более, чем в 2 раза худший оптимального. 3. Возможен алгоритм построения пути по минимальному скелету, который также дает время работы не более, чем в 2 раза худшее оптимального. 4. Популярным способом решения задачи является «оптимизированный» перебор или «метод ветвей и границ», при котором пытаются отсечь заведомо неэффективные пути. Этот метод дает хорошие результаты на практике, однако, в вырожденных случаях (например, полный граф, все ребра которого имеют единичную нагрузку) сводится к полному перебору. a d e b f c h 10.58 15.86 6.58 9.4 11.4 13.4 S=4 g Жадный алгоритм на каждом шаге пытается добавить в имеющийся цикл одну вершину, ближайшую к циклу. Этот алгоритм хорошо работает в случае полного графа. Мы не получили оптимального маршрута. Оптимальный маршрут имеет сумму S = 14.7. Время работы алгоритма пропорционально n2log n Алгоритм «минимального скелета» для задачи коммивояжера a Сначала построим минимальный скелет, начав с произвольной вершины. d e b f c h g Теперь построим обход получившегося дерева (который НЕ есть гамильтонов цикл). Далее будем спрямлять этот путь, убирая вершины, встречающиеся на этом пути дважды. Получили путь длиной S = 18.6, что тоже хуже, чем оптимальный путь с длиной S = 14.7 Заметим, что спрямление пути – это, фактически, обход дерева в глубину, поэтому его можно получить быстрее, чем мы это делали. Время работы алгоритма определяется временем построения минимального скелета. Для случая полного графа (как в нашем случае) – это O(n2), что лучше, чем для жадного алгоритма увеличения цикла. Результат, однако, получился хуже. Легко видеть, что двойное прохождение минимального скелета не хуже, чем вдвое хуже оптимального гамильтонова пути, а если неравенство треугольника выполнено, то спрямления всегда не ухудшают длину пути.









