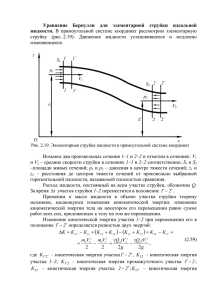
9. Уравнение Бернулли
реклама

Лекция 4 Ранее была получена система уравнений: 2 2 2 v y v y v y 1 p v y v y v y vx vy vz (7.1) x 2 x y z y 2 z 2 y 2 v z 2 v z 2 v z 1 p v z v z v z vx vy v z 2 2 g 2 x y z z x y z 2v v x v x v v 2 v x 2 v x 1 p v x x v y x v z 2x t x y z y 2 z 2 x x v y t v z t Уравнения (7.1) есть дифференциальные уравнения Навье1 – Стокса2 движения вязкой жидкости, являющиеся математическим описанием полей скоростей и давлений в подвижной среде. Конечно же, мы повсеместно имеем дело с реальными жидкостями. Но многие закономерности поведения жидкостей удобно изучать на идеализированной модели — модели идеальной жидкости. 8. Дифференциальные уравнения Эйлера движения идеальной жидкости Идеальная жидкость — воображаемая жидкость, обладающая следующими свойствами: 1. Она не оказывает сопротивления движению, то есть она не обладает внутренним трением ( 0). 2. Она абсолютно несжимаема, то есть её объём, а значит, и плотность не зависят от давления (p). 3. Она не изменяет объём с изменением температуры (Т). Так как идеальная жидкость не обладает внутренним трением, то в её потоке поля скоростей и давлений будут описываться системой дифференциальных уравнений: Навье Луи Мари Анри (H. Navier; 1785-1836), франц. инженер и учёный. В 1822 г. впервые вывел уравнения движения несжимаемой вязкой жидкости. 2 Стокс Джордж Габриель (J. G. Stokes; 1819-1903), англ. физик и математик, член (с 1851 г.) и президент (в 1885-1890 г.г.) Лондонского королевского общества. В 1845 г. вывел уравнения движения для газа. 1 1 dv x p ; dt x dv y p ; (8.1) dt y dv p z g , dt z где проекции ускорений на соответствующие оси координат записаны в «сжатой» форме. Эти уравнения впервые были получены в 1755 году Леонардом Эйлером и называются дифференциальными уравнениями Эйлера движения идеальной жидкости. Если жидкость неподвижна, то уравнения (8.1) упрощаются до вида: p 0; x p 0; (8.2) y p g 0. z Уравнения (8.2) называются дифференциальными уравнениями Эйлера покоя (статики) жидкости. Леонард Эйлер родился 15 апреля 1707 года в швейцарском городе Бáзель в семье сельского пастора. Получив неплохое домашнее образование, Эйлер поступил в старшие классы гимназии и в то же время начал посещать лекции по математике в университете. Талант юного математика был замечен Иоганом Бернулли, который начал заниматься с ним индивидуально. В 17 лет Эйлер уже получил степень магистра искусств. В 1727 году Эйлер прибыл по приглашению в только что учреждённую Петербургскую Академию наук, где сначала стал адъюнктом, а в 1731 году (в возрасте 24 лет!) – профессором по математике. В Петербурге Эйлер жил и работал с 1727 по 1741 г. и с 1766 г. до конца жизни. Эйлер привнёс бесценный вклад в развитие Российской науки. За годы работы в России он подготовил около 400 научных работ; полное собрание его сочинений составляет 72 тома. Леонард Эйлер был не только талантливым и плодотворным учёным, но и человеком самоотверженным. Вот только один факт из его биографии. В 1738 году срочно потребовалось провести трудоёмкие, астрономические расчёты для составления карт Российской Империи. Группа академиков требовала на их выполнение несколько месяцев… Блестящий вычислитель, Леонард 2 Эйлер сделал всю работу за трое суток. Но какой ценой! В результате осложнения после тяжёлого нервного переутомления он потерял зрение правым глазом (когда ему было всего-то 30 лет), а постепенное развитие катаракты на левом глазу привело к тому, что в 59 лет он окончательно ослеп. Но, как в литературе Гомер, так в математике Эйлер был подлинно «слепец всевидящий». Эйлер скончался в 1783 году и похоронен в Петербургском некрополе. Для решения тех или иных задач гидравлики дифференциальные уравнения Эйлера следует проинтегрировать. Интегрирование дифференциальных уравнений Эйлера движения идеальной жидкости приводит к уравнению Бернулли. 9. Уравнение Бернулли Будем считать, что имеет место такое движение жидкости, при котором давление в какой-либо точке пространства, занятого идеальной жидкостью, с течением времени не изменяется. Для выполнения процедуры интегрирования уравнений Эйлера (8.1) предварительно умножим каждое уравнение, соответственно, на vx, vy и vz. Тогда интегрированию подлежат уравнения вида: dv x p vx ; dt x dv y p vy vy ; dt y dv z p vz v z g v z . dt z vx (9.1) Поскольку компоненты скоростей можно представить в виде v x dx , dt dy dz и v z , то соответствующая замена в правых частях уравнеdt dt ний и умножение всех слагаемых на dt приводит к системе: vy p dx; x p v y dv y dy; y p v z dv z dz g dz. z v x dv x (9.2) 3 Просуммируем правые и левые части всех трёх уравнений: ( v x dv x v y dv y v z dv z ) p p p dx dy dz g dz. y z x Преобразуем это уравнение. Его левая часть может быть представлена в виде: ( v x dv x v y dv y v z dv z ) (9.3) v 2 v 2y v 2 v x2 v 2y v z2 (9.4) d x d d z d 2 2 2 2 2 2 v v d . d 2 2 В соответствии с допущением о неизменности давления во времени, то есть, считая, что p (x, y, z), имеем выражение для полного дифференциала этой функции: p p p (9.5) dp dx dy dz . x y z Тогда, с учётом (9.4) и (9.5), уравнение (9.3) может быть записано в виде: v2 d 2 dp g dz , (9.6) или v2 0, dp g dz d 2 или, заменяя сумму дифференциалов дифференциалом суммы, v2 0. d p g z 2 Интегрируя это уравнение, получаем: p g z v2 const . 2 (9.7) (9.8) (9.9) Уравнение (9.9) называется «интеграл Бернулли» или «уравнение Бернулли для элементарной струйки идеальной жидкости». 4 Даниил Бернулли принадлежал к семье известных швейцарских учёных. Он родился в 1700 году в Гронингене (Нидерланды), а вскоре семья Иоганна Бернулли – отца Даниила (и учителя Леонарда Эйлера(!)) – переехала в Базель, где Даниил сначала окончил гимназию, а затем изучал философию и логику в местном университете. Уже в 16 лет он получил степень магистра философии, в 21 год – степень лиценциата медицины. В это же время он опубликовал свою первую серьёзную научную работу – книгу «Математические упражнения». В 1725 году Даниил вместе с братом Николаем прибыл по приглашению формировавшейся Академии Наук в Петербург. 8 лет работал Даниил Бернулли в Петербургской Академии, и это были годы наибольшего творческого подъёма. Однако, и покинув Россию, Д. Бернулли не прерывал связи с Петербургской Академией Наук, но уже в качестве её иностранного члена. В целом в изданиях Академии вышло 50 работ Д. Бернулли из 75 его научных трудов. Именно в Петербурге Бернулли подготовил первый вариант рукописи своего главного труда: «Гидродинамика или записки о силах и движении жидкости». Кстати, этой работой Д. Бернулли ввёл в науку термин "гидродинамика". Окончательный вариант этой книги был опубликован на латинском языке в 1738 году, в Страсбурге. Однако ещё в 1726 году Даниил Бернулли выступил с докладом на одном из заседаний Петербургской Академии Наук, и в этом докладе, среди прочего, был опубликован ставший теперь классическим принцип гидродинамики, согласно которому: «в струе воды или воздуха давление велико, если скорость мала, и давление мало, если скорость велика». Уравнение Бернулли является, по существу, одной из форм закона сохранения энергии. Энергетический смысл слагаемых уравнения Бернулли становится очевидным из следующих рассуждений, приводимых применительно к элементарной частице жидкости объёмом dV, или массой dm dV, или весом dG dmg g dV. Для того чтобы поднять (переместить) на высоту z элементарную частицу жидкости объёмом dV, необходимо произвести работу против силы тяжести, равную W = dGz gdVz. (9.10) При этом на эквивалентную величину увеличивается потенциальная энергия частицы: Еп W +gdVz . (9.11) Следовательно, удельная (отнесённая к единице объёма) потенциальная энергия положения будет определяться значением: Еп, z g dV z g z , [Дж/м3] = [Па]. (9.12) dV dV 5 За счёт давления р элементарная частица жидкости объёмом dV может быть поднята на высоту h p/(g). При этом производится работа против силы тяжести, равная: dGh gdVh, и потенциальная энергия частицы увеличивается на эквивалентную величину: +gdVh g dVp/(g) dVp. (9.13) Следовательно, удельная (отнесённая к единице объёма) потенциальная энергия давления будет определяться значением: Eп, р dV р (9.14) p , [Дж/м3] = [Па]. dV dV Очевидно, первые два слагаемые уравнения Бернулли в сумме определяют удельную потенциальную энергию элементарной частицы жидкости. Наконец, элементарная частица жидкости массой dm dV, движущаяся со скоростью v, обладает кинетической энергией: Eк dmv22 dVv22. (9.15) Следовательно, удельная (отнесённая к единице объёма) кинетическая энергия элементарной частицы будет определяться значением: E к dV v 2 / 2 v 2 , [Дж/м3] = [Па]. (9.16) dV dV 2 Величина v2/2 именуется также «динамическое давление». В соответствии с уравнением Бернулли сумма потенциальной и кинетической энергий элементарной струйки остаётся неизменной во всех сечениях. Если каждое слагаемое уравнения (9.9) разделить на ускорение свободного падения g, то можно получить уравнение Бернулли в форме: p v2 z const , (9.17) g 2g где каждое слагаемое уравнения есть удельная энергия единицы массы жидкости. Наконец, если каждое слагаемое уравнения (9.9) разделить на постоянное произведение g, то получим уравнение Бернулли в форме: z p v2 const , g 2g (9.18) где каждое слагаемое уравнения есть удельная энергия единицы веса жидкости, а именно: z — нивелирная (геометрическая) высота расположения сечения элементарной струйки жидкости над некоторой плоскостью сравнения, или удельная потенциальная энергия положения, [м] [Дж/Н]; 6 p/(g) — пьезометрическая высота, пропорциональная давлению в рассматриваемом сечении, или удельная потенциальная энергия давления столба жидкости, [м] [Дж/Н]; v2/2g — высота столба жидкости, эквивалентная высоте, с которой в вакууме должна свободно (без начальной скорости) упасть элементарная частица жидкости, чтобы приобрести скорость v, или удельная кинетическая энергия, [м] [Дж/Н]. И вновь отмечаем, что для элементарной струйки идеальной жидкости удельная энергия есть величина постоянная, одинаковая во всех сечениях струйки. В гидравлике удельная энергия единицы веса жидкости называется «гидравлическим напором», или просто – «напором», и обозначается символом Н (от англ. head – напор). Тогда величины z, p/(g) и v2/2g могут рассматриваться как, соответственно, геометрический напор, пьезометрический напор и динамический напор жидкости. И уравнение Бернулли показывает, что при установившемся движении идеальной жидкости сумма геометрического, пьезометрического и динамического напоров в каждом поперечном сечении элементарной струйки есть величина постоянная, то есть Н const. В дополнение к сказанному заметим, что при прекращении движения, то есть при v 0, уравнение Бернулли обращается в основное уравнение гидростатики: (9.19) p g z const . 10. Некоторые практические приложения принципа и уравнения Бернулли Несмотря на то, что принцип Бернулли и его уравнение относятся к течению идеальной (невязкой) жидкости, они используются для решения некоторых практических задач, связанных с течением реальных жидкостей, но лишь в случаях, когда внутренним трением можно пренебречь. 1. На принципе Бернулли основана работа струйных насосов. Всем хорошо известна конструкция водоструйного насоса. (Водоструйный насос изобрёл в 1868 г. Роберт Бунзен, более известный как изобретатель газовой горелки.) В этом устройстве поток рабочей жидкости (например, воды) проходит сначала конфýзор (сопло) — конический сужающийся элемент, имеющий на конце отверстие 2 мм. В конфузоре за счёт уменьшения диаметра увеличивается скорость потока, уменьшается давление, так что в месте выхода рабочей жидкости из конфузора создаётся разрежение. В 7 камере смешения рабочая жидкость смешивается с перекачиваемой средой (например, воздухом), увлекает её за собой и далее поступает в диффýзор — конический расширяющийся элемент насоса. В диффузоре вследствие уменьшения скорости кинетическая энергия смеси преобразуется в потенциальную энергию давления, необходимую для дальнейшего перемещения жидкости. В технике струйные насосы получили название инжекторы и эжекторы. Инжекторы — насосы, предназначенные для сжатия газов и паров, а также для нагнетания жидкостей в различные аппараты. Эжекторы — насосы, предназначенные для отсасывания газов, паров или жидкостей. 2. На принципе Бернулли основана работа некоторых приборов для измерения скорости и расхода жидкости. I) Трубка Пито–Прандтля В названии прибора фигурирует имя французского математика, физика и гидротехника, члена Парижской академии наук (с 1724 г.) Анри Питó (H. Pitot; 1695-1771). В 1732 г. он опубликовал сочинение «Описание одного прибора для измерения скорости воды, текущей струёй из сосуда», в котором показал, что если в поток воды в канале опустить трубку, загнутую навстречу потоку (см. рис. 6), h то вода в трубке поднимается выше уровня воды в самом канале. При этом v высота подъёма воды в трубке (h) проро р порциональна скорости потока (v). Однако измерение скоростей потоРис. 6 ков в напорных трубопроводах с помощью только трубки Пито технически невозможно, так как за счёт повышенного давления жидкость может подниматься на значительную высоту. (Как известно, давление в 1 избыточную атмосферу поднимает воду на 10 м!) В связи с этим в начале XX века немецкий учёный Людвиг Прандтль предложил дополнить конструкцию второй трубкой, отверстие которой параллельно линиям тока. Измеряя разность давлений в этих двух трубках, можно рассчитать скорость потока. Для получения расчетной зависимости рассмотрим горизонтальную трубку тока, упирающуюся своим концом в отверстие трубки Пито. Вдали от отверстия жидкость, имеющая плотность L, течёт со скоростью v; давление в жидкости равно р. У преграды (у отверстия трубки Пито), то есть в критической точке, давление равно ро, а скорость потока vo = 0. 8 Запишем уравнение Бернулли для этой элементарной струйки: v2 v2 pg z L po g zo L o , (10.1) 2 2 откуда, учитывая, что z = zo, а vо = 0, v2 po p L . (10.2) 2 Скорость, а, следовательно, и давление вблизи отверстия трубки Прандтля практически не отличаются от скорости и давления в невозмущённом потоке. Таким образом, в двух трубках прибора создаётся разность давлений, равная р L v 2 2 . Эту разность давлений можно измерить, например, U-образным дифференциальным манометром, заполненным манометрической жидкостью с плотностью м. При фиксируемой разности уровней манометрической жидкости в коленах дифманометра, равной hм, в соответствии с уравнением гидростатики имеем: p (м L ) g hм . Отсюда: м L . (10.3) L Индекс «i» у символа скорости здесь показывает, что определена скорость i-ой элементарной струйки, то есть локальная скорость потока в месте установки датчика (трубки Пито). Измерив скорости в различных точках, можно определить среднюю скорость потока по формуле (4.5), а зная последнюю — расход жидкости по формуле (4.6). vi 2 g hм II) Дроссельные устройства К дроссельным устройствам относятся мерная диафрагма, мерное сопло, труба Вентури и др. Мерная диафрагма (рис. 7) представляет собой устройство, которое имеет тонкий металлический диск Д с центральным круглым отверстием, имеющим заострённую кромку. Диаметр отверстия диафрагмы do меньше диаметра d трубы Т, на которой устанавливается диафрагма. Диск диафрагмы с обеих сторон зажимается металлическими кольцами К, внутренний диаметр которых равен диаметру d трубопровода Т. В наиболее распространённом варианте исполнения диафрагмы в указанных кольцах выполнены кольцевые камеры, усредняющие по поперечному сечению потока давление р до диафрагмы и давление ро за отверстием в диске. 9 При монтаже на трубопроводе мерная Д К Т Ф диафрагма укрепляется между фланцами Ф, приваренными на труd d do do бе Т. Мерное сопло (рис. 8) — деталь специального профиля, имеющая плавно зар ро р ро круглённый вход и цилиндрическое выходное Рис. 7 Рис. 8 отверстие диаметром do, меньше диаметра трубы d. Труба Вентури3 (рис. 9) — конструкp po ция, имеющая на входе цилиндрический учаРис. 9 сток, затем — конфузор (сходящийся усечённый конус), цилиндрическое горло и диффузор (расходящийся конус). Длины цилиндрических участков равны их диаметрам. Отборы давлений р и ро производятся в серединах цилиндрических элементов конструкции. Как видим, названные устройства различаются конструктивно, но являются однотипными по принципу действия. В узких местах этих дроссельных приборов скорость потока возрастает пропорционально квадрату уменьшения диаметра, а давление — понижается от величины р [до устройства] до величины ро [в узком месте]. Измерив, например, дифференциальным манометром, возникающую разность давлений, можно оценить скорость течения жидкости. Формула для расчёта скорости потока в трубе диаметром d имеет вид: 1 v 2 ghм м d 4 4 1 . do (10.4) Вентури Джованни Батиста (G. Venturi; 1746-1822), итал. учёный. В 1797 г. опубликовал исследование об истечении воды через короткие цилиндрические и расходящиеся насадки. В 1887 г. амер. учёным В. Гершелем был предложен водомер, названный именем Вентури. 3 10 Формула (10.4) получена на основе предположения об идеальности жидкости. Фактически дроссельные устройства используются для измерения скоростей реальных (вязких) сред, в связи с чем правая часть формулы умножается на коэффициент расхода дроссельного прибора (α), значение которого индивидуально для каждого устройства и определяется по соответствующим справочникам. Всем хорошо известна история, произошедшая с пароходом «Титаник». И мало кто знает об истории, случившейся несколько ранее с его аналогом – пароходом «Олимпик». Однажды этот океанский лайнер проплывал по водам одной из бухт, а в это же время рядом с ним параллельным курсом шёл крейсер «Гаук». Неожиданно «Гаук» повернул на 90° и на полном ходу врезался в борт «Олимпика», учинив в нём пробоину. Капитан «Гаука» был обвинён в нарушении законов лоции, и подвергнут суду. Впоследствии удалось доказать, что истинным «виновником» происшествия являлся… принцип Бернулли. Дело в том, что суда двигались на небольшом расстоянии друг от друга, и в пространстве между ними давление воды понизилось. В результате повышенная с одной стороны сила давления воды на борт судна развернула корабль, что и привело к катастрофе. Кстати, некоторые историки полагают, что вскоре «травмированный» «Олимпик» и «здоровый» «Титаник» поменялись именами. То есть на ледяные глыбы напоролся латанный, бывший «Олимпик»! По той же самой причине (по причине уменьшения давления в потоке среды) категорически запрещается находиться вблизи железнодорожного полотна, по которому с большой скоростью движется состав. Материал подготовил В. Н. Бобылёв 11