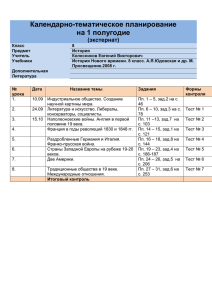
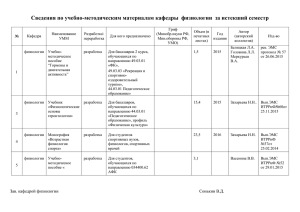
Уравнение механического равновесия

Модели замкнутых
электромеханических систем
Для того, чтобы разработать модель
замкнутой ЭМС необходимо составить:
Систему уравнений, описывающих
процессы в элементах системы;
Структурные схемы отдельных элементов
системы;
Иметь представление о функциональном
назначении этих элементов в составе
функциональной схемы замкнутой
электромеханической системы;
Модель замкнутой
электромеханической системой
с П-регулятором
В замкнутой ЭМС с пропорциональным (П)
регулятором, двигателем постоянного тока
независимого возбуждения
и широтноимпульсным преобразователем обратная
связь осуществляется за счет датчика
скорости, которым обычно служит
тахогенератор.
Структурная
схема
такой
ЭМС
имеет
следующий вид:
Система уравнений
Система дифференциальных уравнений
(СДУ), описывающая данную ЭМС,
состоит из трех уравнений:
• уравнение электрического равновесия
якорной цепи ДПТ НВ;
• уравнение движения электропривода;
• уравнения состояния ШИП.
При составлении уравнения состояния ШИП
внесем для удобства коэффициент
передачи регулятора kР в передаточную
функцию
преобразователя.
Тогда
коэффициент передачи ШИП будет равен
произведению kПР ⋅ kР , причем
U (t )  U (t )  U зад (t ) - U ос (t )  U зад (t )  kпр  kос  ω(t ).
Уравнение состояния преобразователя:
dU d (t )
Tпр 
 U d (t )  kпр  kр  (U зад  U ос )  kпр  kр  (U зад  kос  kтг   (t )).
dt
Уравнение электрического равновесия
ДПТ НВ:
di(t )
U d (t )  Lдв 
 R дв i (t )  c  ω(t ).
dt
Уравнение механического равновесия
ДПТ НВ:
d  (t )
c  i (t )  M с  J дв 
.
dt
Разрешая
каждое
уравнение
относительно производных, запишем
СДУ в нормальной форме Коши:
 dU d (t ) 1
  [kпр  kр  (U зад  kос  kтг  ω(t ))  U d (t )]

dt
T
пр


di (t ) 1

 [U d (t )  R дв i (t )  c  ω(t )]

dt
L
дв


d (t ) 1

 [c  i (t )  M с ]

dt
J дв

Математическая модель ЭМС с
П- регулятором
Математической моделью ЭМС является
СДУ в векторно-матричной форме
представленная в виде:
dX (t )
 A  X (t )  B 1(t )
dt
где
U d (t ) 
X (t )   i(t )  - вектор переменных состояний
 ω(t ) 
 kпр  kр  U зад

Tпр

В 
0

Mс

 J
дв



 - вектор свободных членов





 1

T
 пр
 1
A
 Lдв

 0


0
Rдв

Lдв
c
J дв
kпр  kр  kос  k тг 


Tпр


c


Lдв



0


- матрица коэффициентов (параметров
ЭМС)
Из полученной математической модели
видно, что помимо двух переменных
состояния двигателя (тока и скорости)
ЭМС
имеет
третью
переменную
состояния – выходное напряжение
ШИП, обусловленную инерционностью
преобразователя.
Модель замкнутой
электромеханической системой
с ПИ-регулятором
Структурная
схема
электромеханической системы с ПИрегулятором, двигателем постоянного
тока
независимого
возбуждения
и
широтно-импульсным преобразователем
имеет следующий вид:
Структурная схема
Уравнения электрического
состояния
В данном случае уравнение равновесия
напряжения, подводимого к обмотке
якоря двигателя имеет вид:
di (t )
U d  Lдв 
 Rдв  i (t )  c  ω(t ),
dt
где напряжение питания двигателя
U d (t )  [kр  (U зад  kос  kтг   (t ))  U уи ]  kпр
К этим двум уравнениям прибавляется
уравнение состояния ПИ-регулятора:
Tр 
dU уи (t )
dt
 U зад  kос  kтг  ω(t ),
где Tp - постоянная времени регулятора.
Уравнение механического равновесия
останется без изменений:
d  (t )
c  i (t )  M с  J дв 
.
dt
Математическая модель ЭМС с
ПИ - регулятором
Математической моделью ЭМС является
СДУ в векторно-матричной форме
представленная в виде:
dX (t )
 A  X (t )  B 1(t )
dt
где
 i (t ) 


X (t )   ω(t ) 
U уи (t ) 


- вектор переменных состояний
 kпр  kр U зад 


Lдв


- вектор свободных членов СДУ


Mс


В

J дв




U
зад




T
р


 Rдв

 Lдв
 c
A
 J дв

 0



kпр  kр  kос  k тг  c
Lдв
0
kос  kтг

Tр
kпр 

Lдв 

0 


0 


- матрица коэффициентов (параметров ЭМС)
В замкнутой электромеханической
системе с ПИ регулятором третьей
переменной состояния выступает
напряжение управления интегральной
частью ПИ-регулятора.