Сложение натуральных чисел Вычитание натуральных чисел

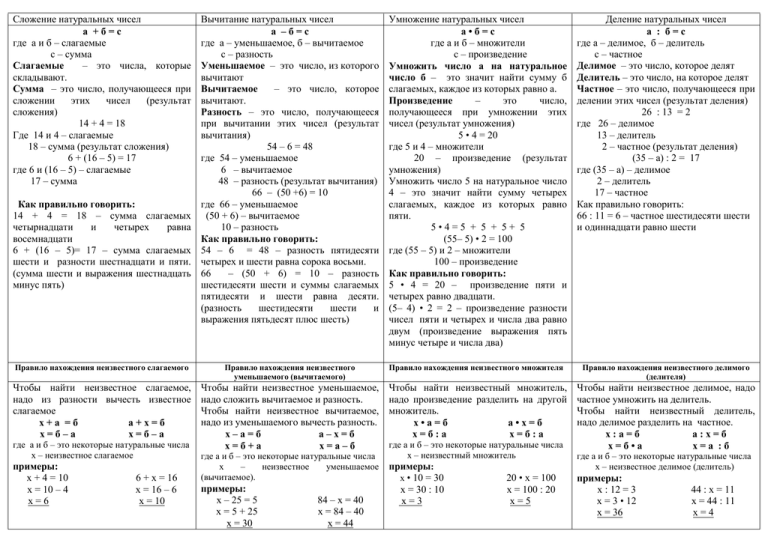
Сложение натуральных чисел
а +б=с
где а и б – слагаемые
с – сумма
Слагаемые
– это числа, которые
складывают.
Сумма – это число, получающееся при
сложении
этих
чисел
(результат
сложения)
14 + 4 = 18
Где 14 и 4 – слагаемые
18 – сумма (результат сложения)
6 + (16 – 5) = 17
где 6 и (16 – 5) – слагаемые
17 – сумма
Вычитание натуральных чисел
а –б=с
где а – уменьшаемое, б – вычитаемое
с – разность
Уменьшаемое – это число, из которого
вычитают
Вычитаемое
– это число, которое
вычитают.
Разность – это число, получающееся
при вычитании этих чисел (результат
вычитания)
54 – 6 = 48
где 54 – уменьшаемое
6 – вычитаемое
48 – разность (результат вычитания)
66 – (50 +6) = 10
где 66 – уменьшаемое
(50 + 6) – вычитаемое
10 – разность
Как правильно говорить:
54 – 6 = 48 – разность пятидесяти
четырех и шести равна сорока восьми.
66
– (50 + 6) = 10 – разность
шестидесяти шести и суммы слагаемых
пятидесяти и шести равна десяти.
(разность
шестидесяти
шести
и
выражения пятьдесят плюс шесть)
Умножение натуральных чисел
а•б=с
где а и б – множители
с – произведение
Умножить число а на натуральное
число б – это значит найти сумму б
слагаемых, каждое из которых равно а.
Произведение
–
это
число,
получающееся при умножении этих
чисел (результат умножения)
5 • 4 = 20
где 5 и 4 – множители
20 – произведение (результат
умножения)
Умножить число 5 на натуральное число
4 – это значит найти сумму четырех
слагаемых, каждое из которых равно
пяти.
5•4=5 + 5 + 5+ 5
(55– 5) • 2 = 100
где (55 – 5) и 2 – множители
100 – произведение
Как правильно говорить:
5 • 4 = 20 – произведение пяти и
четырех равно двадцати.
(5– 4) • 2 = 2 – произведение разности
чисел пяти и четырех и числа два равно
двум (произведение выражения пять
минус четыре и числа два)
Деление натуральных чисел
а : б=с
где а – делимое, б – делитель
с – частное
Делимое – это число, которое делят
Делитель – это число, на которое делят
Частное – это число, получающееся при
делении этих чисел (результат деления)
26 : 13 = 2
где 26 – делимое
13 – делитель
2 – частное (результат деления)
(35 – а) : 2 = 17
где (35 – а) – делимое
2 – делитель
17 – частное
Как правильно говорить:
66 : 11 = 6 – частное шестидесяти шести
и одиннадцати равно шести
Правило нахождения неизвестного слагаемого
Правило нахождения неизвестного
уменьшаемого (вычитаемого)
Правило нахождения неизвестного множителя
Правило нахождения неизвестного делимого
(делителя)
Чтобы найти неизвестное слагаемое,
надо из разности вычесть известное
слагаемое
х+а =б
а+х=б
х=б–а
х=б–а
Чтобы найти неизвестное уменьшаемое,
надо сложить вычитаемое и разность.
Чтобы найти неизвестное вычитаемое,
надо из уменьшаемого вычесть разность.
х–а=б
а–х=б
х=б+а
х=а–б
Чтобы найти неизвестный множитель,
надо произведение разделить на другой
множитель.
х•а=б
а•х=б
х=б:а
х=б:а
Чтобы найти неизвестное делимое, надо
частное умножить на делитель.
Чтобы найти неизвестный делитель,
надо делимое разделить на частное.
х:а=б
а:х=б
х=б•а
х=а :б
Как правильно говорить:
14 + 4 = 18 – сумма слагаемых
четырнадцати
и
четырех
равна
восемнадцати
6 + (16 – 5)= 17 – сумма слагаемых
шести и разности шестнадцати и пяти.
(сумма шести и выражения шестнадцать
минус пять)
где а и б – это некоторые натуральные числа
х – неизвестное слагаемое
примеры:
х + 4 = 10
х = 10 – 4
х=6
6 + х = 16
х = 16 – 6
х = 10
где а и б – это некоторые натуральные числа
х
–
неизвестное
уменьшаемое
(вычитаемое).
примеры:
х – 25 = 5
х = 5 + 25
х = 30
84 – х = 40
х = 84 – 40
х = 44
где а и б – это некоторые натуральные числа
х – неизвестный множитель
примеры:
х • 10 = 30
20 • х = 100
х = 30 : 10
х=3
х = 100 : 20
х=5
где а и б – это некоторые натуральные числа
х – неизвестное делимое (делитель)
примеры:
х : 12 = 3
х = 3 • 12
х = 36
44 : х = 11
х = 44 : 11
х=4