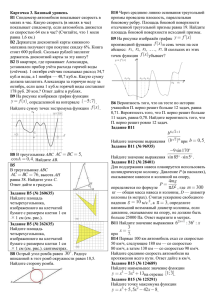
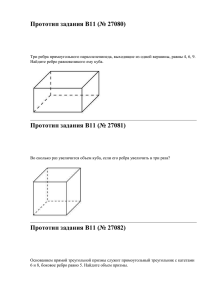
fg(x1,x2,...,xn)
реклама

ПРОЕКТИРОВАНИЕ АВИАЦИОННЫХ КОНСТРУКЦИЙ Аналитические модели проектирования: - параметрический метод оптимизации варьируемых параметров или конструктивный метод оптимизации Математически всю процедуру оптимизации конструкции по массе можно представить в следующем виде. Имеется функция n конструктивных искомых параметров (целевая функция): m=m(x1,x2, ... ,xn) при наличии ограничений на эти параметры fi(x1,x2, ...,xn)=0 i=1,2,...,k; fg(x1,x2,...,xn)=0 g≤1,2,...,p x1≥0, x2≥0, ... ,xn≥0 Критерии оптимальности. Такие критерии, как правило, не соответствуют строго критерию минимума массы. Наиболее известным и простым является критерий равнопрочности. Согласно ему из всех конструкций, воспринимающих данную нагрузку и изготовленных из заданного материала, минимальной массой обладает та, для которой напряженное состояние в каждой точке принадлежит поверхности разрушения Условие оптимальности структуры: 12 0 Коэффициент безопасности при проектировании конструкции из композиционных материалов и критерии прочности • • Наиболее используемые критерии прочности имеют полиномиальный вид, в котором чаще всего учитываются два первых члена в форме (k) = Fii + Fijij 1, k, i, j = 1,2,…6, где Fi и Fij - тензоры прочности 2 и 4 ранга. Чаще используется квадратичный критерий в виде 2 F11 12 F12 1 2 F22 22 F66 12 1 или 1i f ( ) 1 • 2 2 2 i i i i 1 2 2 12 min 1 2 2 12 С учетом знаков и величин пределов прочности 1 1 1 1 i 1 1 1 2i 2 2 2 ( 1i ) 2 12i ( 2i ) 2 1; 1 1 2 2 12 i 1, n. • • Для однонаправленной ленты : - для волокна 2 2 - для связующего . i 2i 12 1 0 в 2 12 1i 1 0, в1 Проектирование крыла кессонного типа Проектирование с использованием условия равнопрочности y Mz 2 5 1 4 7 Mx z 3 6 Qy x Целевой функцией является масса сечения. Два этапа проектирования Этап 1. Он включает в себя определение структуры, толщины слоев в каждой панели, считая их плоскими пластинами и удовлетворяя трем ограничениям: - ограничение по прочности; - ограничение по крутильной жёсткости сечение крыла; - ограничение по изгибной жесткости сечения крыла. 1 00 , 2,3 / 4, 4 / 4 2,3,5,6 – углы укладки укладки , для панелей 1,4,7 углы 2,3 / 4, 4 / 4 , а усилия определяются приближенно по Qy 0 Mx Mz 0 0 0 0 q 3. Q ,r Nz , N zs qК , qК формулам H BH 2B H r 1 После определения толщин нулевого приближения находим усилия следующего M x B11,r , где y J ox 7 Sy 7 J oxy Sx 2 y , x , F hr lr B11, r J ox B11,r y ds, y y y0 ( x x0 ) , x x x ( y y )J / J 0 0 F F 0 0 oxy ox r 1 r J oy r 1 приближения N z ,r k 7 S x B11, r y ds, 7 S y B11,r xds r 1 r 1 , где n a q a к 1 kj k hi( k 1) Qj k k akj k 7 J oy B11, r x ds ds , , B33,r 2 r 1 r aQj k 7 J oxy B11, r x y ds r 1 r qQ . Толщины находим из ds B33,r 1 sin i cos i ) 2 2 N zs E h (cos i sz sin i ) N z G h 1 z zs hi E1i 1 b1 2 2 (sin cos ) N i zs i s E h s (k ) • Погонный угол закручивания находится с помощью теоремы Кастильяно и U записывается в форме • Ограничение по изгибной жесткости x U 1 N z ,r yds xпр M k J ox i r E z ,r hr i Оптимальные свойства однонаправленного материала 2i E 2i (1 21 ) в структуре материала конструкции i 1i E1i (1 21 ) Для тканных материалов лучше использовать критерий типа Хилла Этап 2. Делается с учетом конкретного членения крыла на отдельные элементы: лонжероны, нервюры, панели, поверхности управления, носовой части и т. п. Проводится перераспределение материала по элементам конструкции (полки лонжерона, стрингеры). I. b ТИПЫ ПАНЕЛЕЙ II. Перераспределение III. нагрузки по элементам сечения крыла IV. а) V б) – сотовая панель. N z N z(1) N z(2) (1) (2) B11 B11 B11 N zi i B11 Проектирование лонжеронов, нервюр, соединений, стыковых узлов Учет обжатия лонжеронов и нервюр при изгибе композитного крыла 2 M N ст x B11,панlн y p EJ x 50-60мм 100-120 мм панели h=5,...,7 мм R=5мм А , а Б Рассмотрена трехстрингерная панель, в которой обшивка и средний подкрепляющий элемент на свободном краю не работают, а вся нагрузка передается через два крайних стрингера. Противоположный край панели закреплен. P y P EF N1(x) a x Nx Ex ,Ey, G, xy, h Nxy N2(x) Ex ,Ey, G, xy, h a EF Nxy Nx N1(x) P P EF l Рис. 1.1 7 Усилия Nx и Nxy в обшивках. По результатам такого решения выявлены наиболее нагруженные области конструкции, в которых ожидается интенсивный процесс накопления повреждений и возможного разрушения. 8 Влияние растрескивания в поперечном слое на напряженное состояние многослойной структуры E2cр (h1 h2 ) E1 h1 1 E2cp ( k ) , E2cp cp ( k ) / cp ( k ) , cp ( k ) h2 2X f 2 cp ( k ) 2W / 2 cp 2 cp 0,5 P /(h1 h2( k ) ) 1 W 2X f Xf Xf Xf 2 dx Xf xi2 zi2 1 x zi z xi i2 2E 2 E E xi zi 2G i 1 h 2 E zi zi i xi xi 3 i dx dz Вторая система трещин Первая система трещин Рис. 2.5 Рис.2.6 9 Изменение механических характеристик Развитие межслойных трещин в окрестности поперечных трещин. 2l 2Xf Рис. • В этом случае реальные характеристики модулях принимаются: E1(1) E10 , E2(1) E20 , G12(1) G120 , E1(2) E10 (1 ) , G12(2) G120 (1 ) . упругости l/Xf Поперечный модуль упругости второго слоя определиться по формуле ( X f l ) [ ] 2 X f h2 2E ( X f l ) (2) 2 20 (2) 2 [ 2(2) ]2 dx dy 2 E20 h2 / 2 h2 / 2 10 Модель поврежденности с учетом поперечного растрескивания и расслоения при циклическом нагружении. • Модель деградации свойств КМ при циклическом нагружении. Система уравнений: dP ds dl v N 0 , C (K ) m C ( ) m ( l ) m / 2 dN dN dN dS ds dP ds S s S p P s( N ) P0 dN dN dN dN • К этой системе уравнений следует присоединить начальные условия: S|N N S0 , S|N N * S* , P| N N P0 , l|N N l0 • 0 0 0 Решение системы уравнений дает величину накопления повреждений: 4 3 4 3 12 N 3 3S* 2 N 3 3S* Se 2 1 0 2 1 1 , Sg 2 1 0 2 1 1 3 N* 3 N* b 2 12 11 НДС Аналитический метод, МКЭ Критерии локалного разрушения Определение зон поврежденности и типов поврежденности ( МКЭ ) модель поврежденности с учетом поперечного растрескивания ( Квазистатический случай ) модель поврежденности с учетом поперечного растрескивания и раслоения ( Квазистатический случай ) Модули упругости поврежденности КМ ( Ex , Ey , Gxy… ) модель поврежденности при циклическом нагружении МКЭ расчет НДС, усилиях и деформациях Критерии разрушения ( деформационный ) 12 Заданы для рассматриваемой конструкции площади стрингеров в см2 и структура панели • Заданы параметры : N*0 1.000.000; S* 1; S0 0,1; • С этими параметрами получили напряжения в слоях обшивке и в слоях стрингера • Получено изменение модуля упругости вдоль оси Ox и модуля сдвига в панели в зависимости от числа циклов рис. рис. • Модуль упругости вдоль стрингера и модуль сдвига в крайних стрингерах в зависимости от числа циклов 13 В месте предложении нагрузки Вдали места предложении нагрузки Используя МКЭ, подставим новые характеристик в структуру получим новый результат: Change deformation F=2,5cm2 11,400 epxilon x 1000 11,300 11,200 11,100 11,000 10,900 10,800 10,700 10,600 0 2000 4000 6000 8000 10000 12000 N Таб. Перерасчет НДС в месте приложения нагрузки крайних стрингерах Рис. Деформации в крайних стрингерах в месте приложения зависит от N ( F3=0,00025м2 , =0,5 ) 14