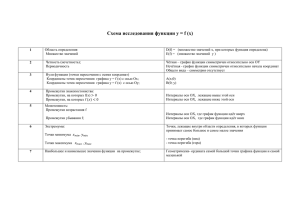
f(х)=1/3x-x³ 1. Областью определения функции являются все
реклама

f(х)=3x-x³ 1. Областью определения функции являются все значения, которые принимает переменная x или аргумент. D(f)=(-∞;+∞) 2. Функция является четной, если для любого x из области определения функции выполняется равенство f(-x)=f(x) Функция является нечетной если для любого x из ее области определения выполняется равенство f(-x)=f(x) f(-x)=3(-x)-(-x)³=-3x+x³=-(3x-x³)=-f(x)-функция является нечетной, непериодическая. 3.Точки в которых график функции пересекается с осью x имеет ординаты равные 0, т.е. F(x)=0, тогда получаем уравнение: 3x-x³=0 x(3-x²)=0 x=0 или x=±√3 f(x) пересекается с осью x в точках (-√3;0) ; (0;0) ; (√3;0) Точка в которой график функции пересекается с осью y имеет абсциссу, равную 0 f(0)=0 f(x) пересекается с осью y в точке (0;0). 4. Промежутки знакопостоянства функции - это промежутки, в которых функция принимает положительные и отрицательные значения. Для нахождения решаем неравенства: f(x)>0 и f(x)<0 3x-x³>0 и 3x-x³<0 f(x)>0 на (-∞;-√3)U(0;√3) f(x)<0 на (-√3;0)U(√3; +∞) 5. Чтобы найти промежутки возрастания и убывания функции находим производную функции f`(x) f`(x)=(3x-x³)`= 3-3x² Функция непрерывна и дифференцируема на всей своей области определения. Находим нули производной f`(x)=0 3-3x²=0 3x²= 3 x²=1 x=±1 Эти точки явл. Критическими точками функции. f`(x)>0 на (-1;1), тогда f возрастает на [-1;1] f`(x)<0 на (-∞;-1)U(1; +∞), тогда f убывает на (-∞;-1] и на [1; +∞) 6.Находим точки экстремума xmin=-1, f(-1)=-2 xmax=1, f(1)=2 7.Построение графика