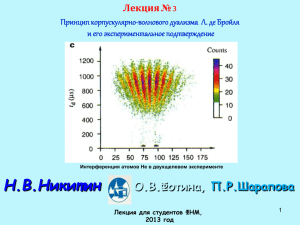
Лекция Корпускулярно-волновой дуализм
реклама

КАФЕДРА ФИЗИКИ КарГТУ 2008 год Слайд-лекция по дисциплине «Физика 2» Корпускулярноволновой дуализм Выполнили: доцент кафедры физики КарГТУ Научный руководитель Орлова Елена Федоровна Филимонова Юлия Шмидт Ирина План лекции: 1. Корпускулярно-волновая природа света. Фотон и его характеристики. 2. Волновые свойства микрочастиц и соотношение неопределенностей Гейзенберга. 3. Формула де Бройля. При излучении проблем теплового излучения Планк эмпирически получил формулу для спектральной плотности энергетической светимости абсолютно черного тела Через некоторое время он объяснил, что тепловое излучение пускается дискретно в виде отдельных порций энергии, средняя энергия которых равна Альберт Эйнштейн Для объяснения ряда закономерностей таких явлений, как фотоэффект, люминесценция, фотохимические реакции А. Эйнштейн (1905) ввёл гипотезу световых квантов, согласно которой электромагнитное излучение состоит из отдельных частиц, квантов излучения, то есть имеет корпускулярно-волновую природу. Позднее эти кванты были названы фотонами (обозначение фотона). Энергия монохроматическом каждого излучении фотона частоты в (и длины волны ) определяется формулой , где h = 6,62610-34 Джс – постоянная Планка или квант действия. Импульс фотона равен: или В векторном виде это соотношение имеет вид: где - волновой вектор. Из уравнения Эйнштейна, следует, что фотон имеет массу, зависящую от частоты и длины волны излучения: m = Согласно СТО масса движущегося фотона определяется формулой Чтобы масса фотона m осталась конечной (при V=c), необходимо предположить, что m0 = 0. Таким образом, фотон – частица, не имеющая массы покоя и существующая только в движении со скоростью света. Опытные данные свидетельствуют, что m 410-21me, где me – масса электрона. Согласно СТО четырехмерный импульса имеет вид: вектор Следовательно, для фотона справедливо соотношение или или По современным представлениям, свет обладает двойственной корпускулярноволновой природой, причём в различных условиях физического опыта он может обнаруживать сходство с потоком частиц либо с распространением волн. Энергия и импульс фотонов равны: Корпускулярно-волновой дуализм микрочастиц.Гипотеза Де Бройля В 1924 г. французский физик Луи де Бройль выдвинул гипотезу, согласно которой установленный ранее для корпускулярно-волновой присущ всем микрочастицам. фотонов дуализм Луи де Бройль (1892-1987) Луи де Бройль, один из создателей квантовой механики - всемирно известный ученый, чьи работы в области теоретической физики, а также выдающийся литературный талант глубоко изменили современную физику и поставили его в один ряд с самыми выдающимися учеными нашего времени. Он первым пришел к выводу, что дуализм волначастица - явление природы, а не ухищрения математиков для преодоления каких-то расходимостей. Его рассчеты волновых свойств частиц были подтверждены экспериментально (дифракция электронов). Луи де Бройль лауреат нобелевской премии за 1929 года по физике за открытие волновых свойств электрона в 1923 году. Таким образом, если частица имеет энергию E и импульс p, то с ней связана некоторая волна, частота которой = и длина = Эти волны получили название волн де Бройля. Для частиц, движущихся со скоростями имеем: p = m = , . Для медленных частиц c и m m0, поэтому . Следовательно, длина волны де Бройля тем меньше, чем больше масса m0 частицы и её скорость . Например, частице с массой покоя в 1 г, движущейся со скоростью 1 м/с, соответствует волна де Бройля с 10-18 Å (10-28 м), что лежит за пределами доступной наблюдению свойства области. Поэтому несущественны макроскопических тел. в волновые механике Волновые свойства электронов проявляются, например, при их рассеянии на тех же кристаллах, на которых наблюдается дифракция рентгеновских лучей. Экспериментально дифракция электронов впервые была обнаружена в опыте американских физиков К. Дэвиссона и Л. Джермера (1927 г.). Распределение отражённых электронов давало максимумы в соответствии с условием Вульфа-Брэгга: 2dsin = k, где d – расстояние между соответствующими кристаллографическими плоскостями, - угол скольжения падающего пучка электронов на данную плоскость, - длина волны де Бройля. Наблюдая лучей дифракцию известной кристаллической длины структуре строения и измеряя рентгеновских волны на неизвестного и m, можно найти межплоскостное расстояние, т.е. определить структуру вещества. Этот метод лежит в основе рентгеноструктурного анализа. Методы исследования структуры вещества, основанные на дифракции электронов и нейтронов, называются электронографией и нейтронографией. Наблюдая дифракцию рентгеновских лучей неизвестной длины волны на кристаллической структуре при известном d и измеряя и m, можно найти длину волны падающего рентгеновского излучения. Этот метод лежит в основе рентгеновской спектроскопии. Соотношения неопределённостей. С уменьшением размеров начинают проявляться качественно новые свойства, не обнаруживающиеся у макрочастиц. Волновая природа электрона (и других микрочастиц) приводит к тому, что в отличие от материальной частицы классической физики электрон не может иметь одновременно точные значения координаты x и соответствующей координате составляющей импульса px. этой Поэтому никакой эксперимент не может привести к точному измерению одновременно обеих этих переменных. При этом произведение неопределённости x координаты x на неопределённость px проекции импульса на ось x должно быть по порядку величины не меньше приведённой постоянной Планка: xpx . Аналогичные соотношения выполняются и для других пар так называемых канонически сопряжённых переменных, так что имеем: xpx , ypy , zpz . Эти соотношения носят название соотношений неопределённостей Гейзенберга (установлены в 1927 г. немецким физиком Вернером Гейзенбергом). Гейзенберг Вернер (5.XII.1901– 1.II.1976 Немецкий физик-теоретик. Один из основателей квантовой механики. Сформулировал (1927) одно из важнейших положений физики – принцип неопределенности. Дал математическое обоснование протонно-нейтронной модели атомного ядра. Ввел концепцию матрицы рассеяния (1943). Труды по квантовой электродинамике, теории поля, квантовой теории ферромагнетизма, философии естествознания. Нобелевская премия (1932). Пусть поток электронов проходит через узкую щель шириной x, расположенную перпендикулярно направлению их движения. В этот же момент вследствие дифракции элетроны отклоняются от первоначального направления и будут двигаться в пределах угла . Следовательно, Подобно тому, как импульс не может быть локализован в пространстве, так и энергия не может быть локализована во времени. Для энергии квантовой системы и времени существует неопределённостей вида Et . соотношение Оно означает, во-первых, что энергию стационарного состояния квантовой системы можно измерить лишь с точностью, не превышающей /t, где t есть длительность процесса измерения. Таким образом, соотношение неопределённостей для энергии и времени может трактоваться как невозможность точного определения энергии квантовой системы времени. за ограниченный интервал КОНЕЦ.