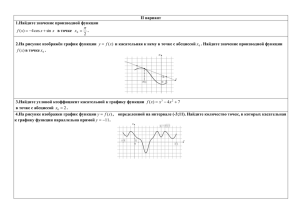
y = f (x)

ЕГЭ –
2015
Прозводная №8
Содержание (виды заданий №8)
1
Найдите значение производной функции в точке х0 по рисунку с изображенным графиком
функции y = f(x) и касательной к нему в точке с абсциссой х0.
2
На рисунке изображен график функции y = f (x), касательная к этому графику, проведенная в
точке х0, проходит через начало координат. Найдите f'(х0).
3
На рисунке изображен график функции y = f (x), определенной на интервале (a; b). Определите
количество целых точек, в которых производная функции отрицательна (положительна).
4
На рисунке изображен график функции y = f (x), определенной на интервале (a; b). Найдите
количество точек, в которых производная функции y = f (x) равна 0.
5
На рисунке изображен график функции y = f (x), определенной на интервале (a; b). Найдите
количество точек, в которых касательная к графику функции параллельна прямой у = с.
6
На рисунке изображен график производной функции f (x), определенной на интервале (a; b).
Найдите точку экстремума функции f (x) .
7
На рисунке изображен график производной функции y = f (x), определенной на интервале
(x1; x2). Найдите количество точек максимума (минимума) функции y = f (x) на отрезке [a;
b].
8
На рисунке изображен график производной функции f(x), определенной на интервале (x1; x2).
Найдите промежутки возрастания (убывания) функции f(x).
9
На рисунке изображен график производной функции f(x), определенной на интервале (x1; x2).
Найдите абсциссу точки, в которой касательная к графику функции f(x) параллельна прямой y =
kx + b или совпадает с ней.
10
11
12
13
14
На рисунке изображён график функции y=F(x) , одной из первообразных некоторой
функции y=f(x), определённой на интервале (x1; x2) . Пользуясь рисунком,
определите количество решений уравнения f(x)=0 на отрезке
[a;b].
Материальная точка движется прямолинейно по закону S=x(t), где x — расстояние
от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В
какой момент времени (в секундах) ее скорость была равна a?
Материальная точка движется прямолинейно по закону S=x(t), где x — расстояние
от точки отсчета в метрах, t — время в секундах, измеренное с начала движения.
Найдите ее скорость (в метрах в секунду) в момент времени t.
Прямая y= kx+d является касательной к графику функции
y=ax2+bx +c . Найдите a (b или c).
На рисунке изображён график некоторой функции y=f(x). Функция F(x) — одна из
первообразных функции . Найдите площадь закрашенной фигуры.
Задача 1.1. На рисунке изображен график функции y = f (x), и
касательная к нему в точке с абсциссой х0. Найдите значение
производной функции y = f (x) в точке х0.
Решение.


А С
f   x0   k  tg ,
BC 3
f   x0   tg 
  3.
AC 1
Ответ: 3.
Теоретические сведения.
Значение производной функции f(x) в точке х0 равно tga — угловому
коэффициенту касательной, проведенной к графику этой функции в данной точке.
Чтобы найти угловой коэффициент, выберем две точки А и В, лежащие на
касательной, абсциссы и ординаты которых — целые числа. Теперь определим модуль
углового коэффициента. Для этого построим ∆ABC. Важно помнить, что тангенс
острого угла прямоугольного треугольника — это отношение противолежащего
катета к прилежащему.
Знак производной (углового коэффициента) можно определить по рисунку,
например, так: если касательная «смотрит вверх» то производная положительна, если
касательная «смотрит вниз» - отрицательна (если касательная горизонтальна, то
производная равна нулю).
Задача 1.2. На рисунке изображен график функции y = f (x), и
касательная к нему в точке с абсциссой х0. Найдите значение
производной функции y = f (x) в точке х0.
б)
a)
А

С
В
А
В
С
Решение.
f   x0   k  tg ,
AC
3
tg (180   )  
   0,5.
BC
6
Ответ: - 0,5 .
f   x0   k  tg ,
AC 3
f   x0   tg 
  0, 75.
AB 4
Ответ: 0,75.
Задача 1.3. На рисунке изображен график функции y = f (x), и
касательная к нему в точке с абсциссой х0. Найдите значение
производной функции y = f (x) в точке х0.
б)
a)

А
А
С
В
С
В
f   x0   k  tg ,
tg (180   )  
Решение.
BC
6
   0, 75.
AC
8
Ответ: - 0,75 .
f   x0   k  tg ,
tg (180   )  
Ответ: - 3 .
AC
6
   3.
BC
2
Задача 2.1. На рисунке изображен график функции y = f (x),
касательная к этому графику, проведенная в точке 4, проходит через
начало координат. Найдите f'(4).
6

Решение.
Если касательная проходит через начало
координат, то можно изобразить ее на
рисунке, проведя прямую через начало
координат и точку касания. В качестве
точек с целочисленными координатами,
лежащих на касательной, можно взять
начало координат и точку касания.
Дальнейшее решение очевидно:
4
f ( x0 )  tg 
Ответ: 1,5.
6
 1,5.
4
Задача 2.2. На рисунке изображен график функции y = f (x),
касательная к этому графику, проведенная в точке х0, проходит через
начало координат. Найдите f'(х0).
Решите самостоятельно!
1
3
х0= 2
х0= - 4

f ( x0 )  tg 
Ответ: 2.

4
2
2
2
f ( x0 )  tg    0,5
4
Ответ: - 0,5.
2
4
х0= 4
х0= - 4

f ( x0 )  tg 
Ответ: 0,5.
2
 0,5
4

f ( x0 )  tg 
3
 0,75
4
Ответ: 0,75.
Задача 3.1. На рисунке изображен график функции y = f (x),
определенной на интервале (-8; 3). Определите количество целых
точек, в которых производная функции отрицательна.
Решение.
f ( x )  0, если f (x ) убывает.
Целые решения:
х=-7; х=-6; х=-2; х=-1.
Их количество равно 4.
Ответ: 4.
Теоретические сведения.
Решим эту задачу, воспользовавшись следующим утверждением. Производная
непрерывно дифференцируемой функции на промежутке убывания
(возрастания) не положительна (не отрицательна). Значит необходимо
выделить промежутки убывания функции и сосчитать количество целых чисел,
принадлежащих этим промежуткам. Причем производная равна нулю на концах
этих промежутков, значит, нужно брать только внутренние точки промежутков.
Задача 3.2. На рисунке изображен график функции y = f (x),
определенной на интервале (—8; 5). Определите количество целых
точек, в которых производная функции положительна.
Решение.
f ( x )  0, если f (x ) возрастает.
Целые решения при : х=-7; х=-6; х=-5; х=-4; х=2; х=3.
Их количество равно 6.
Ответ: 6.
Задача 3.3. На рисунке изображен график функции y = f (x),
определенной на интервале (a;b). Определите количество целых
точек, в которых производная функции положительна.
Решите самостоятельно!
б)
a)
Решение.
f ( x )  0, если f (x ) возрастает.
Целые решения при :
Целые решения при :
х=-2; х=-1; х=5; х=6.
х=2; х=3; х=4; х=10; х=11.
Их количество равно 4.
Их количество равно 5.
Ответ: 4.
Ответ: 5.
Задача 3.4. На рисунке изображен график функции y = f (x),
определенной на интервале (a;b). Определите количество целых
точек, в которых производная функции отрицательна.
a)
б)
Решите самостоятельно!
Решение.
f ( x )  0, если f (x ) убывает.
Целые решения при :
Целые решения при :
х=2; х=7; х=8.
х=-1; х=0; х=1; х=2; х=9; х=10.
Их количество равно 3.
Их количество равно 6.
Ответ: 3.
Ответ: 6.
Задача 4.1. На рисунке изображен график функции y = f (x),
определенной на интервале (-6; 8). Найдите количество точек, в
которых производная функции y = f (x) равна 0.
Решение.
f ( x0 )  0,
если касательная,
проведенная в эту точку
имеет вид у = const.
Считаем количество точек
пересечения графика
функции с касательной.
Ответ: 7.
Теоретические сведения.
Производная функции в точке х0 равна 0 тогда и только тогда, когда
касательная к графику функции, проведенная в точке с абсциссой х0,
горизонтальна. Отсюда следует простой способ решения задачи —
приложить линейку или край листа бумаги к рисунку сверху горизонтально
и, двигая «вниз», сосчитать количество точек с горизонтальной касательной.
Задача 4.2. На рисунке изображен график функции y = f (x),
определенной на интервале (a; b). Найдите количество точек, в
которых производная функции y = f (x) равна 0.
Решите устно!
1
Ответ: 7.
3
Ответ: 7.
4
2
Ответ: 8.
Ответ: 6.
Задача 5.1.
На рисунке изображен график функции y = f (x),
определенной на интервале (-8; 3). Найдите количество точек, в которых
касательная к графику функции параллельна прямой у = 8.
Решение. Прямая у = 8 — горизонтальная, значит, если касательная к
графику функции ей параллельна, то она
тоже горизонтальна.
Следовательно, при решении этой задачи можно воспользоваться решением
задачи 2, то есть приложить линейку или край листа бумаги горизонтально
и, двигая его «вниз», сосчитать количество точек с горизонтальной
касательной.
Ответ: 5.
Задача 5.2. На рисунке изображен график функции y = f (x),
определенной на интервале (a; b). Найдите количество точек, в
которых касательная к графику функции параллельна прямой у = с.
1
Ответ: 4.
Решите устно!
3
Ответ: 8.
4
2
Ответ: 9.
Ответ: 9.
Задача 6.1. На рисунке изображен график производной функции f (x),
определенной на интервале (—7; 5). Найдите точку экстремума функции
f (x) на отрезке [-6; 4].
-6
+ -3
-
4
Решение.
Отметим на рисунке границы отрезка, о котором идет речь в условии задачи.
На этом отрезке производная функции один раз обращается в 0 (в точке -3)
и при переходе через эту точку меняет знак, откуда ясно, что точка -3 и есть
искомая точка экстремума функции на отрезке.
Ответ: -3.
Задача 6.2. На рисунке изображен график производной функции f (x),
определенной на интервале (a; b). Найдите точку экстремума функции f (x)
.
Решите устно!
1
3
-3
4
Ответ: -3.
Ответ: 4.
4
2
7
-1
Ответ: 7.
Ответ: -1.
Задача 7.1. На рисунке изображен график производной функции y = f
(x), определенной на интервале (-3; 8). Найдите количество точек
минимума функции y = f (x) на отрезке [-2; 7].
4,5
+
-
Решение.
В точке минимума производная функции равна нулю либо не существует.
Видно, что таких точек на отрезке [-2; 7] три: —1,5; 4,5; 6,5. При этом в точке 4,5
производная слева отрицательна, а справа положительна, значит, это точка
минимума. В точках -1,5 и 6,5 производная меняет знак с «+» на «—» это точки
максимума.
Ответ: 1 .
Задача 7.2. На рисунке изображен график производной функции
y = f (x), определенной на интервале (x1; x2). Найдите количество
точек максимума функции y = f (x) на отрезке [a; b].
Решение.
1
Найдем точки в которых
f   x   0. Это: -3; 3; 5.
a
+
-
b
x0 - точка максимума, если
производная при переходе
через x0 меняет свой знак с
плюса на минус.
Условие выполняется в
точке x = 3.
Ответ: 1 .
2
Решение.
a
+ -
b
+ - + -
Решение аналогично.
Условие выполняется в
точках: -1; 8; 13.
Ответ: 3 .
Задача 7.3. На рисунке изображен график производной функции
y = f (x), определенной на интервале (x1; x2). Найдите количество точек
экстремума функции y = f (x) на отрезке [ -3; 10 ].
1
Ответ: 4 .
2
Ответ: 4 .
Задача 8.1. На рисунке изображен график производной функции y = f
(x), определенной на интервале (-11; 3). Найдите промежутки
возрастания функции f(x). В ответе укажите длину наибольшего из
них.
-10
-1
-7
2
6
Решение.
В этой задаче необходимо сначала найти промежутки возрастания функции,
т.е. промежутки на которых f´(x) > 0.
В нашем случае их три: (-11; -10), (-7; -1) и (2; 3), наибольшую длину из
них, очевидно, имеет промежуток (-7; -1), его длина равна:
-1-(-7) = 6.
Ответ: 6 .
Задача 8.2. На рисунке изображен график производной функции f(x),
определенной на интервале (x1; x2). Найдите промежутки убывания
функции f(x). В ответе укажите длину наибольшего из них.
1
6
-4
-10
Решение.
Найдем промежутки
убывания функции, т.е.
промежутки на которых
f´(x) < 0.
Наибольшую длину из них
имеет промежуток (-10; -4)
Ответ: 6 .
2
3
Решение.
Решение аналогично: ищем
промежутки на которых f´(x)
< 0.
Наибольший из них имеет
длину равную 3.
Ответ: 3 .
Задача 8.3. На рисунке изображен график производной функции f(x),
определенной на интервале (x1; x2). Найдите промежутки возрастания
функции f(x). В ответе укажите длину наименьшего из них.
3
Решение.
Найдем промежутки
возрастания функции, т.е.
промежутки на которых
f´(x) > 0.
Наименьшую длину из них
имеет промежуток (-2; -1).
Ответ: 1 .
4
Решение.
Решение аналогично: ищем
промежутки на которых f´(x)
> 0.
Наименьший из них имеет
длину равную 2.
Ответ: 2 .
Задача 9.1. На рисунке изображен график производной функции f(x),
определенной на интервале (-11; 3). Найдите количество точек, в
которых касательная к графику функции f(x) параллельна прямой y =
2x -5 или совпадает с ней.
y=2
Решение.
Если касательная к графику функции f(x) параллельна прямой y = 2x-5 или
совпадает с ней, то ее угловой коэффициент равен 2, а значит нам нужно найти
количество точек, в которых производная функции f(x) равна 2.
Для этого на графике производной проведем горизонтальную черту,
соответствующую значению y = 2, и посчитаем количество точек графика
производной, лежащих на этой линии. В нашем случае таких точек 5.
Ответ: 5 .
Задача 9.2. На рисунке изображен график производной функции f(x),
определенной на интервале (x1; x2). Найдите количество точек, в
которых касательная к графику функции f(x) параллельна прямой y = 2x + 7 или совпадает с ней.
1
y = -2
Решение.
Касательная к графику функции f(x)
параллельна прямой y = -2x+7 или
совпадает с ней, то ее
угловой
коэффициент равен -2.
Найдем количество точек, в которых
f´(x)= -2.
Ответ: 3 .
2
y = -2
Решение.
Поступим аналогично, найдем
количество точек, в которых f´(x)=
-2.
Ответ: 4 .
Задача 9.3. На рисунке изображен график производной функции f(x),
определенной на интервале (x1; x2).
3
y=2
Найдите количество точек, в которых
касательная к графику функции f(x)
параллельна прямой y = 2x +10 или
совпадает с ней.
Решение.
Найдем количество точек, в которых
f´(x)= 2.
Ответ: 3 .
4
y = -3
Найдите количество точек, в которых
касательная к графику функции f(x)
параллельна прямой y = -3x+8
или
совпадает с ней.
Решение.
Найдем количество точек, в которых
f´(x)= -3.
Ответ: 3 .
Задача 9.4. На рисунке изображен график производной функции f(x),
определенной на интервале (x1; x2). Найдите абсциссу точки, в которой
касательная к графику функции f(x) параллельна прямой y = 7 - 4x или
совпадает с ней.
Решение.
5
2
y = -4
Для того чтобы найти искомую абсциссу,
выясним, в какой точке f´(x) = - 4. Для этого
проведем горизонтальную прямую y = - 4 и
найдем абсциссу точки пересечения этой прямой
с графиком производной. Она и будет искомой
абсциссой точки касания.
Ответ: 2 .
Решение.
6
-1
y = -4
Поступим аналогично, найдем точку, в которой f´(x)
= - 4, проведем горизонтальную прямую y = - 4 и
найдем абсциссу точки пересечения этой прямой с
графиком производной.
Ответ: -1 .
Задача 10.1 На рисунке изображен график функции y=F(x), одной из
первообразных некоторой функции f(x) ,определенной на интервале
(-3;5). Пользуясь рисунком, определите количество решений уравнения
f(x)=0 на отрезке [-2;4]
Решение.
Поскольку F(x), - первообразная
функции f(x) – это функция, производная
которой равна f(x) : F/(x)= f(x) – исходную
задачу можно переформулировать так: по
графику функции найти количество точек,
принадлежащих отрезку [-2;4], в которых
производная функции равна нулю.
Как мы знаем, производная равна нулю в
точках экстремума.
Отметим на рисунке сам отрезок и точки
экстремума на графике функции.
Точки экстремума («холмики» и
«впадинки») выделены красным цветом. На
отрезке [-2;4] их 10.
Ответ: 10.
, где
Задача 11.1. Материальная точка движется прямолинейно по закону
x(t)=t3 -9t2 -8t-5, где x
— расстояние от точки отсчета в метрах, t —
время в секундах, измеренное с начала движения. В какой момент времени
(в секундах) ее скорость была равна 40м/с?
Решение.
Физический смысл производной - если зависимость расстояния от
времени представляет собой функцию S(x), то, чтобы найти скорость тела
в момент времени t0, нужно найти значение производной
функции S(x) в точке t0 : v(t0 )= S /(x)
x(t)=t3 -9t2 -8t-5
x / (t)=3t2 -18t – 8
3t2 -18t – 8=40
t1 = 8
t2= -2 не удовл.
Ответ: 8 .
Задача 12.1. Материальная точка движется прямолинейно по закону
, где x
— расстояние от точки отсчета в
метрах, t — время в секундах, измеренное с начала движения. Найдите ее
скорость (в метрах в секунду) в момент времени
Решение.
x / (t)=2t3 - 12t2+ 2.
x / (6)= 2∙63 -12 ∙62 + 2 = 2
Ответ: 2 .
t=6 с.
у = -3х+4 является касательной к графику
функции ах2 + 27х +10 . Найдите a.
Задача 13.1. Прямая
Теоретические сведения.
Прямая является касательной к параболе. если имеет с ней одну общую точку.
Решение.
Чтобы найти точку пересечения прямой и параболы нужно
составить и решить систему уравнений
у=-3х+4
у=ах2 + 27х +10
ах2 + 27х +10= -3х+4
ах2 +30х+6=0
Мы получили квадратное уравнение, которое имеет единственный корень,
если дискриминант равен нулю. Приравняем дискриминант к нулю:
D= 302 -4∙a∙6 = 900-24a=0
a= 37,5
Ответ: 37,5 .
Задача 13.2 Прямая у=-3х+1 является касательной к графику
функции 25х2 + bх +10. Найдите b, учитывая, что абсцисса точки касания
больше 0.
Решение.
Чтобы найти точку пересечения прямой и параболы нужно
составить и решить систему уравнений
у=-3х+1
у=25х2 + bх +10
25х2 + bх +10 =-3х+1
25х2 +(b+3)x +9 =0
Мы получили квадратное уравнение, которое имеет единственный
корень, если дискриминант равен нулю. Приравняем дискриминант
к нулю:
D= (b+3)2- 4∙25∙9 = b2 +6b -891=0
b1 = -33
b2 = 27
Производная функции в точке касания равна коэффициенту
наклона прямой
b1 = -33
b2 = 27
50x +b=-3
x= -3-b
50
при
x1 = 0,6
x2 = -0,6
Ответ: 0,6 .
Задача 13.3 Прямая у=-7х-1 является касательной к графику функции
2х2 + х +с. Найдите с
Решение.
Чтобы найти точку пересечения прямой и параболы нужно
составить и решить систему уравнений
у=-7х-1
у=2х2 + х +с
2х2 + х +с= -7х-1
2х2 +8х+(с+1)=0
Мы получили квадратное уравнение, которое имеет единственный корень,
если дискриминант равен нулю. Приравняем дискриминант к нулю:
D= 82 -4∙2∙(с+1) = 81-8с-8=73-8с=0
с= 9,125
Ответ: 9,125 .
Задача 14.1 На рисунке изображён график некоторой функции y=f(x).
Функция F(x)=2x3 +60x2+602x – 1,25 — одна из первообразных
функции y=f(x). Найдите площадь закрашенной фигуры.
Теоретические сведения.
Определенный интеграл
–
это число, равное площади
криволинейной трапеции – фигуры,
ограниченной сверху графиком
положительной на
отрезке [a;b] функции , слева
прямой x=a, справа прямой x=b, и снизу
осью ОХ.
Решение.
Закрашенная фигура представляет собой криволинейную трапецию,
ограниченную сверху графиком функции y=f(x) , слева прямой x =-11, справа
прямой x=-9 , и снизу осью ОХ.
S=F(-9)-F(-11) = (2(-9)3 +60(-9)2+602∙(-9) – 1,25) - (2(-11)3 +60(-11)2+
+602∙(-11) – 1,25) =-2017,75-(-2025,75)=8
Ответ: 8 .
Задача 14.2. На рисунке изображён график некоторой функции y=f(x) (два
луча с общей начальной точкой). Пользуясь рисунком, вычислите
F(6)-F(2), где F(x) — одна из первообразных функции y=f(x) .
Решение.
Определенный интеграл – это ЧИСЛО, значение которого вычисляется
по формуле Ньютона – Лейбница, равное площади криволинейной трапеции :
S=S1 + S2 =2∙3 + (1∙2):2 = 7
Ответ: 7 .