ИНТЕГРАЦИЯ ФИЗИКИ, МАТЕМАТИКИ И ИНФОРМАТИКИ СРЕДСТВАМИ НОМОГРАФИИ НА УРОВНЕ ПРЕДВУЗОВСКОГО ОБРАЗОВАНИЯ
реклама

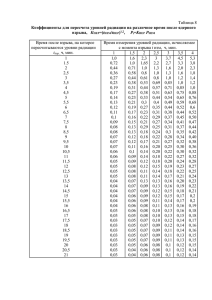
ИНТЕГРАЦИЯ ФИЗИКИ, МАТЕМАТИКИ И ИНФОРМАТИКИ СРЕДСТВАМИ НОМОГРАФИИ НА УРОВНЕ ПРЕДВУЗОВСКОГО ОБРАЗОВАНИЯ Кузнецова Татьяна Ивановна (Москва, Центр международного образования МГУ имени М.В. Ломоносова) Математика дает возможность с помощью математических моделей описывать самые разнообразные реальные процессы и предсказывать результаты, к которым они приводят. Л.Д. Кудрявцев. Среднее образование. Проблемы. Раздумья. Номограммы – это считающие чертежи. Это модели функциональных зависимостей. Разработана методика преподавания основ номографии в средней школе. Доказана возможность демонстрации эффективности номографических методов не только в математике, но в других школьных дисциплинах, а также то, что использование и построение номограмм, организованное в средней школе, повышает математическую культуру учащихся, под которой понимается «…определенный запас знаний, навыков и умений учащихся, в том числе и умение применять накопленные знания и навыки в трудовой и учебной деятельности» (С.И. Шварцбурд). Сетчатые номограммы – часто применяются и в математике, и в физике, и вообще в самых разных областях науки А.Н. Колмогоров П р и м е р. Уравнение Ван-дер-Ваальса, которое связывает объем (v) реального газа, его давление (p) и температуру (T): (p a )(v - b) RT 2 v Изотермы (T=const) Номограмма из выравненных точек – для решения уравнения 1 1 1 x y z В.М. Брадис «Четырехзначные математические таблицы», с. 82 «Оптика» Формула тонкой линзы «Электричество» Формула общего сопротивления при параллельном соединении 1 1 1 F d f 1 1 1 R R1 R2 F — фокусное расстояние d — расстояние от предмета до линзы f — расстояние от изображения до линзы R — общее сопротивление R1, R2 — сопротивления участков Применение ромбоидальных и транспарантных номограмм в расчете точечного взрыва в газе в точке пространства с геометрической координатой r в момент времени t (считая от момента взрыва) Исходные данные: E0 — энергия взрыва, p — давление газа до взрыва, — плотность газа до взрыва, RГ — газовая постоянная, — показатель адиабаты, величина определяет характер взрыва: 1 — плоский взрыв, 2 — цилиндрический, 3 — сферический; Искомые: давление p, плотность , скорость v, температура T, полная энергия в единице объема E. t (q) E p 0 1 p p p p 1 2 (1) (3) r 0 (q) i 1 E 0 Rn (q) p p 1 f 1 ( q ) g 1 ( q, i ) q (4) f 2 ( q ) g 2 ( q, i ) (2) (3′) (4′) v p v (5) v 1 g 3 ( q, i ) q (5′) T p T RГ (6) T 1 f 4 ( q ) g 4 ( q, i ) q (6′) (7) E 1 f 5 ( q ) g 5 ( q, i ) q (7′) E p E Таблицы для вспомогательной безразмерной переменной q и вспомогательных безразмерных функций (q), Rn(q), 0 (q), f1 (q), f2 (q), f4 (q), f5 (q), g1 (q, i), g2 (q, i), g3 (q, i), g4 (q, i), g5 (q, i) Таблица 1 Таблица 2 Номографирование расчета точечного взрыва в газе сводит решение задачи к простым геометрическим операциям. Расчет осуществляется с помощью двух номограмм — ромбоидальной и транспарантной. Неподвижная плоскость Транспарант Расчет номограмм произведен на компьютере по специально составленным программам, предусматривающим квадратичную, а иногда и третьей степени, интерполяцию по соседним узловым точкам таблиц, допускаемую этими таблицами. Важно отметить, что использование номограмм не только существенно упростило решение задачи, но и позволило наглядно проследить изменение ответных величин в зависимости от изменения заданных параметров, что невозможно сделать по таблицам. Таким образом, рассчитанные на компьютере таблицы и предложенные номограммы дополняют друг друга и позволяют быстро исследовать и полностью решить сложную задачу расчета газодинамических функций точечного взрыва в газе.