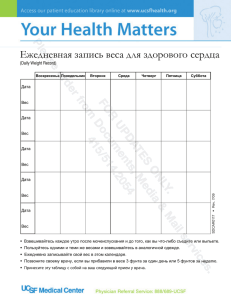
Скейлинговая гипотеза
реклама

Скейлинговая гипотеза ( Для описания перехода металл-изолятор ? При Т=0 ? ) Корреляционная длина x Управляющий параметр Функция состояния Проводимость s [W -1cm 2-d] Кондактанс Y [W -1] Безразмерный кондактанс y Y s L d -2 L - ребро куба Y s Ld -2 y 2 2 e e Скейлинговая теория перехода металл-изолятор d ln y = d ln L Два возможных предела при L= x 1 s = const I. Металл L= 0 yc y ln y = const + (d-2) ln L yx ln y d ln y d -2 d ln L s II. Изолятор d= 3 -1 2 d = =1 d L y y0 e -L 0 x d ln y d L ln y - L const ln y x d ln L dL E.Abrahams, P.W.Anderson, D.C.Licciardello, and T.W.Ramakrishnan, Phys.Rev.Lett. 42, 673 (1979) Рассуждения Таулесса Стыковка 2d гиперкубов объемом Ld каждый в один гиперкуб объемом (2L)d. i Ei j Ej E ~ ( g d Ld ) -1 2L L Ld По теории возмущений i ~ i 0 cij j 0 J J d cij ~ ~ J ( gd L ) ~ nd Ld Ei - E j W При изменении размера L изменения волновых функций зависит от интеграла перекрытия J, как и изменения проводимости Это отношение входит в критерий Андерсона d=3 Уравнение прямой d ln y = d ln L L= x 1 L>x yc du s(u - uc ) dx d ln y s ln y yc d ln L L= 0 u=ln y, x=lnL u - uc Uesx Решение y yx ln y ln y 3 d= В точке ln yx ln yc 1 const s s L y ln yc yc =1 и ln yx /yc = 1/s. Отсюда yx A e2 Yx A e2 1 s A x Величину x можно выразить через y x s ln yc -1 s , т.е. x при y yc Проводимость s может быть сколь угодно малой d=3 T К р и т и ч е с к а я о б л а с т ь s T 1 /2 s T s e x p [(T T )] 0/ m s Т о ч к ап е р е х о д а x c x 1 x На диаграмме (х,Т) переход металл-изолятор изображается изолированной точкой, которую можно обойти В критической области вблизи квантового фазового перехода не один, а два масштаба: x и Lj Критическая область L j <x T T = 0: 1/x x Le e L hopp Точка перехода x= 2 2 (kFl) + 1) e s = - ( --h l Lee 2 1 + -1 ) e s=-(h x Lee x Область прыжковой проводимости m s exp [- (T0 /T) ] Область Друде xc 2 1 e s=-hx s=0 0 Предел Мотта d=3 x1 -1 x = l=kF 1/l Квантовая поправка x 2 (kFl)2 e s = - --h l 1/x d=3 Функция s(T) в критической окрестности В металлической области при Т = 0 В окрестности перехода при Т = 0 Интерполяционная формула e2 1 1 s x LT s e2 g F D Соотношение Эйнштейна x e2 1 s s 03 LT e2 1 s x e2 1 1 s x LT 1 e2 s (Tg F ) 3 LT D , T d = 3 (эксперимент) 40 25 Ge:As 17 10 3.58 3.50 3.00 0.4 0.8 1.2 1/3 1/3 T (K ) 1.6 I.Shlimak, M.Kaveh,R.Ussyshkin, et al., Phys.Rev.Lett. 77,1103 (1996) -1 0 2 15 3 -1 4.60 4.45 4.17 3.91 3.82 -3 1 5.15 s (W cm ) s (W-1cm-1) 20 5.38 20 0 17 4.6 ·10 cm -3 n [10 cm ] 30 Ge:As 10 B= 4 T 5 5 7T 8T 6 0 0 0.2 0.4 0.6 0.8 T (K1/3) 1/3 1.0 1.2 I.Shlimak, M.Kaveh,R.Ussyshkin, et al., Phys.Rev.B 55,1303 (1997) Температурная зависимость 2D-кондактанса n kF2 e2 LT s s 02 - ln l ne2l e2 s 02 (k F l ) k F Оценка критической температуры: s=0 k F l ln LT l LT x l exp( kF l ) Взяв в качестве LT длину межэлектронной расфазировки, получим Tx D x2 LT D , T exp[ -2(kF l )] Даже не очень большие значения kFl ~ 10 приводят к нереально большим значениям x и нереально малым Tx Отсюда - «металлические пленки» Ларкин, Хмельницкий, ЖЭТФ 83, 1140 (1982) 2D: вместо перехода - кроссовер При kFl ~ 1 значения x и Tx становятся реальными Сильная локализация T 2 Lj (T ) e s2 - - ln h l T 1 2 x Слабая локализация n s0 exp [- (T0 / T ) ] l TL L Crossover 2 В отличие от Tx , не содержит экспоненциально малого множителя Increase of disorder TL /L 1 /x 1 d = 2 (эксперимент) (a) ~ y Подгонка T0 106 T0=1K GaAs /AlxGa1-xAs 10 cm-2 12 8 102 y/y00 (h/e2) 10 6 (b) ln (T/T0) 2 ~ y 6.0111 cm-2 -2 10 0 0.5 1.0 T (K) 1.5 F.W. van Keuls et al., Phys.Rev. B 56,13263 (1997) 2.0 (c) 0 -2 ~ y -4 4 1 ln(y/y00) 0.6 111 4 2 0 -6 -4 -2 0 2 ln (T/T0) -6 -8 0 100 200 T0/T Пленки Cu/Ge, Ag/Ge и Au/Ge 0.3-20 А S.-Y.Hsu and J.M.Valles, Jr., Phys.Rev.Lett. 74,2331 (1995) d = 2 (эксперимент) 3 10 -doped GaAs 2 10 R (MW) Сильная локализация Полоска шириной 500 А Слабая локализация 10 0.1 T0 0.1 1 10 T (K) 100 Yu.Havin,M.Gershenson, and A.Bogdanov, Phys.Rev. B 58,8009 (1998) d = 2 (эксперимент) Si 103 10 -2 102 13.7 2 (h/e ) МОП-структура на поверхности Si ....... n [10 cm ] =7.12 10 1 10-1 0 2 4 T (K) 6 S.V.Kravchenko, W.E.Mason, G.E.Bowker, et al., Phys.Rev. B 51,7038 (1995) 8 Проекция формул слабой локализации на скейлинговую диаграмму Спин-орбитальное взаимодействие 2 j e s 2 d ln y =d ln L dt 3 - t so 1 - 2 2e t dlny =dlnL y2 0 ln y y0 yc y1 2 d= 2 d= Оценка для точки перехода : * k F l ln so Переход не произойдет, если so* exp( k F l ) so so* , т.е. so e k Fl lny T 1x Рост беспорядка / 1 x x 2 s0 exp [- (T0 / T )n ] Активационная проводимость T 2 Lj (T ) e s02 - - ln h l Идеальная система 0 xc= 0