реклама

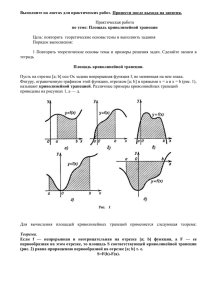
Задача о площади криволинейной трапеции
y
B
y=f(x)
f(ξi)
A
ξ1 ξ2 ξ3
ξi
a x1 x2 xi-1
ξn
xi b
x
n
Sn
f ( )x
k
k
k 1
Эта сумма выражает площадь ступенчатой фигуры, состоящей из
прямоугольников, и приближенно заменяет криволинейную трапецию.
n
Площадью криволинейной трапеции является
S
lim
max x k 0
f ( )x
k
k 1
k
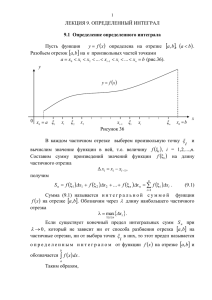
Определение определенного интеграла
Пусть функция y=f(x) определена на [a, b].
1). Разобьем [a, b] на n частей точками x1 < x2
< … < xk <…< xn-1.
T={a=x0, x1, x2, …, xn=b} называется разбиением на
отрезке [a, b], каждый отрезок [xk-1, xk] называется элементарным,
xk = xk – xk-1 – их длина.
2) На каждом элементарном отрезке [xk-1, xk] выберем точку k произвольно!!!
(k ∈ xk).
3) Вычислим f(k) ∈ k.
4) Составим произведение f(.k) xk , k 1, n
Множество
5) Запишем интегральную сумму
(T , )
n
f ( x ) x
k
k
k 1
6) Перейдем к пределу так, что max x k 0
– интегральная сумма
Римана
Определенным интегралом или интегралом Римана на отрезке [a, b]
называется предел интегральной суммы при n→∞
b
n
f ( x)dx lim (T , ) lim f ( )x
0
a
0
i
i 1
i
(1)
Теорема 1. Необходимый признак интегрируемости
Если функция y=f(x) интегрируема на отрезке [a,
этом отрезке.
b], то она ограничена на
Следствие: если функция не ограничена на отрезке [a, b], то она не
интегрируема на [a, b].
Пример. Доказать, что функция Дирихле не интегрируема на отрезке [a,
Функция Дирихле
b].
1 , x Q ( множеству рациональных чисел)
f ( x)
0 , x J ( множеству иррациональных чисел)
Основные свойства определенного интеграла.
a
1.
f ( x)dx 0
a
2.
3.
4.
a
a
b
f ( x)dx f ( x)dx
b
b
a
a
k f ( x)dx k f ( x)dx
b
b
b
a
a
a
f ( x) g ( x)dx f ( x)dx g ( x)dx
b
5.
b
c
b
f ( x)dx f ( x)dx f ( x)dx
a
a
c
каково бы ни было расположение точек
a,b,c.
6. Если функция y=f(x) интегрируема и неотрицательна на [a,
b] и a<b, то
b
f ( x)dx 0
a
7. Если две функции y=f(x) и y=g(x) интегрируемы на [a,
f(x) ≤ g(x) для любого x ∈ [a, b], то
b
b
a
a
f ( x)dx g ( x)dx
8.
b], a<b и
g(x)
y
f(x)
b
b
a
a
f ( x)dx f ( x) dx
a
b
x
x
9. Если функции y=f(x) непрерывна
на [a, b], a<b и ∀ x∈[a, b]
выполняется m
≤ f(x )≤ M , то
y
M
f(x)
m
b
m(b a)
f ( x)dx M (b a)
a
a
10. Теорема о среднем
Пусть функция y=f(x) интегрируема
на [a, b] и ∀x∈[a, b] выполняется
m ≤ f(x )≤ M , тогда
b
x
x
b
x
x
f(x)
y
f(c)
b
f ( x)dx (b a)
a
a
Геометрически: при некотором значении с
c
∈ [a, b] f(с) = .
Площадь под
кривой f( x ) ≥ 0 – площадь криволинейной трапеции – равна площади
прямоугольника с тем же основанием и высотой, равной среднему значению
функции на этом отрезке.
f(с) = – среднее значение функции.
Достаточные условия интегрируемости (классы интегрируемых функций)
Теорема 2. Если функция
y=f(x) определена и непрерывна на [a,b], то она
интегрируема на [a,b].
Теорема 3. Если функция
y=f(x)
монотонна и ограничена на [a,b], то она
интегрируема на [a,b].
Теорема 4. Если функция
y=f(x)
имеет конечное число точек разрыва
первого рода на [a,b], то она интегрируема на [a,b].
y
y=f(x)
a
b
x
Определенный интеграл с переменным верхним пределом.
y=f(x) интегрируема на [a, b] тогда она
интегрируема на любом отрезке [a, x], где a ≤ x ≤ b и имеет смысл
Опр. 2. Пусть функция
интеграл
x
f (t )dt J ( x)
(2)
a
J(x) определена на [a, b] и называется интегралом с переменным
верхним пределом.
Теорема 5. Пусть функция
b]. Определенный
интеграл с переменным верхним пределом от непрерывной на [a, b]
функции y=f(x) является первообразной для подынтегральной
функции f(x)
то есть
y=f(x) непрерывна
на [a,
J ( x) f ( x) x [a, b] ( 3 )
x
(Или функция
J ( x) f (t )dt
a
имеет производную
x [a, b]
причем
J ( x) f ( x))
Следствие
Теорема 5*.
Всякая непрерывная функция имеет непрерывную первообразную
Теорема 6. (Ньютона-Лебница)
Если F(x)
- какая-либо первообразная
от непрерывной функции y=f(x) , то справедлива формула
b
f ( x)dx F ( x)
b
a
F (b) F (a)
(4)
a
b
a
- знак подстановки. Читают
F(x)
от
a
до
b.
Замечание. Формула Ньютона-Лейбница справедлива и для кусочнонепрерывных функций.
Методы вычисления определенного интеграл
- Табличное
b
- Интегрирование по частям
UdV UV
b
b
a
a
- Интегрирование методом подстановки
Теорема 7. Пусть функция
b
y=f(x) непрерывна
VdU
a
на [a,
b] и дан интеграл
f ( x)dx
a
Введем новую переменную
Если
1)
2)
3)
t по формуле x = j (t)
j(a) = a, j (b) = b
j(t) и j'(t) непрерывны на [ a, b ]
f [j (t)] определена и непрерывна на [a, b ] то
b
b
a
f ( x)dx
a
f (j (t ))j (t )d t
Интегралы по симметричному промежутку от четной и нечетной функции.
Теорема 7. Пусть
a
y=f(x) непрерывная четная
на [- a, a] функция, тогда
y
a
f(x)
f ( x)dx 2 f ( x)dx
a
S1
0
S2
-a
Теорема 8. Пусть
y=f(x) непрерывная нечетная
a
на [- a,
a
a] функция, тогда
y
a
f ( x)dx 0
f(x)
-a
S+
a x
S-
x