РТФ РАДИОТЕХНИЧЕСКИЙ ИНСТИТУТ

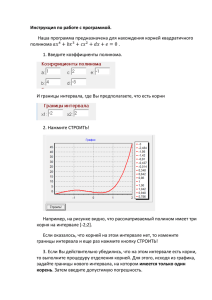
РАДИОТЕХНИЧЕСКИЙ ИНСТИ
РТФ
«Вычислительная математика»
Презентационные материалы к лекциям :
Селиванова Ирина Анатольевна,
ст.преподаватель кафедры
«Автоматики и информационных
технологий» УГТУ-УПИ
РЕАЛИЗАЦИЯ АЛГОРИТМОВ ЛИНЕЙНОЙ АЛГЕБРЫ.
Вычисление корней алгебраических многочленов
•
•
•
•
•
•
•
•
•
•
•
•
•
•
1. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ПОЛИНОМАХ
1.1. Основные определения
1.2. Формы представления полиномов
1.3. Постановка задач
2. МЕТОДЫ ВЫЧИСЛЕНИЯ КОРНЕЙ ПОЛИНОМОВ
2.1. Графический метод определения вещественных корней
2.2. Сравнение погрешностей для простого и кратного корня
приближенного полинома
2.3. Вычисление корней полиномов второй и третьей степени
2.4. Уточнение корней полинома методом Ньютона
2.5. Метод Берстоу уточнения квадратичного делителя полинома
2.6. Схема Горнера
2.7. Метод Рыбакова вычисления всех вещественных корней
2.8. Метод сопровождающей матрицы
СПИСОК ЛИТЕРАТУРЫ
1. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ПОЛИНОМАХ
1.1. Основные определения
Полиномом, или многочленом, называется функция вида
Pn ( x)  a 0  x n  a1  x n 1    a n
(1)
где n - степень полинома, х – аргумент, a0, …,an – коэффициенты, a0≠0.
Число x1 называется корнем полинома Pn(x), если оно удовлетворяет
равенству Рn(x1)=0.
Вычисление корней является наиболее распространенной и в то же
время наиболее сложной операцией с полиномами. По самому
своему определению полином представляет собой сумму членов
k
a k  x. nПри
вида
больших по модулю значениях x и для полиномов
высокой степени некоторые из таких членов могут быть большими.
В то же время нахождение корня связано с определением такого
значения x, при котором полином, т.е. сумма его членов,
обращается в ноль.
НАЧАЛЬНЫЕ СВЕДЕНИЯ О ПОЛИНОМАХ
1.2. Формы представления полиномов
Каноническая форма
Форма представления полинома в виде (1), данная при его
Pn ( x)  a 0  x n  a1  x n 1    a n
определении:
называется канонической. Коэффициент a0 обычно предполагается
отличным от нуля, при этом n – наивысшая степень аргумента x
называется степенью полинома. Фактически задание полинома в
канонической форме сводится к заданию вектора коэффициентов
(a0 , a1 , , a n ) .
Форма разложения
Хорошо известным является способ разложения функции в
степенной ряд. Если разложение ведется в окрестности точки a и
ограничивается конечным числом членов, то возникает функция
S n ( x)  b0 ( x  a) n  b1 ( x  a) n1    bn
(2)
Формы представления полиномов
Факторизованная форма
Факторизованной будем называть форму представления
Pn ( x)  Rm ( x)  S nm ( x)
(3)
где Rm и Sn–m – многочлены, степени которых меньше n (0 < m < n).
Полностью факторизованная форма
Полином представляется в виде произведения линейных множителей
n
(4)
Pn ( x)  a0 ( x  x1 )( x  x 2 )  ( x  x n )  a0  ( x  xi )
i 1
где x1,…, xn – все его корни. Это представление также называют
представлением корнями.
Полностью факторизованная форма с учетом кратностей корней
Среди корней x1, x2,…, xn полинома (4) могут быть совпадающие.
Группируя члены, содержащие одинаковые корни, полином можно
представить в виде
Pn ( x)  a0 ( x  x1 ) r ( x  x2 ) r ( x  x s ) r
(5)
где числа r1, r2,…,rs – называются кратностью соответствующих корней,
причем r1+ r2+…+rs = n. Если rj= 1 для какого-либо j, то j-ый корень
называется простым.
1
2
s
Формы представления полиномов
R-факторизованная форма полинома с комплексными корнями
Возьмем в (4) пару линейных множителей, соответствующих
сопряженным корням. Пусть ( x  xk )( x  xk 1 ), причем xk 1  xk . Тогда
квадратичный полином d 2 ( x)  ( x  xk )( x  xk 1 )  x 2  ( xk  xk 1 ) x  xk xk 1  x 2  ax  b
имеет вещественные коэффициенты a   xk  xk 1  ( xk  xk ) ,
b  xk xk 1  xk xk .
Группируя попарно скобки с комплексно-сопряженными корнями в (4)
и оставляя в неизменном виде линейные множители с
вещественными корнями, можно представить полином в виде
произведений квадратичных и линейных сомножителей с
вещественными коэффициентами:
Pn ( x)  a 0 ( x 2  a1 x  b1 )  ( x 2  a k x  bk )( x  x 2 k 1 )  ( x  x n )
(6)
НАЧАЛЬНЫЕ СВЕДЕНИЯ О ПОЛИНОМАХ
1.3. Постановка задач
Сегодня существует огромное множество проблем, так или иначе
требующих
использования
алгебраических
многочленов.
Различные задачи, связанные с полиномами, требуют применения
различных форм их представления.
Различные формы представления полиномов теоретически
равносильны. Однако на практике некоторая несогласованность
может иметь место. Кроме того, практические преобразования
всегда сопровождаются потерей точности в результате ошибок
округления. Для полиномов высокой степени ошибки округления
зачастую могут приводить к непредсказуемым результатам.
Остановимся на одном из наиболее важных аспектов – нахождении
корней полиномов, так как именно это зачастую доставляет
наибольшие трудности, особенно для многочленов степени n>3.
Для них не существует готовых формул для нахождения корней,
поэтому необходимо использовать итерационные методы
вычисления. Рассмотрим различные виды таких методов.
2. МЕТОДЫ ВЫЧИСЛЕНИЯ КОРНЕЙ ПОЛИНОМОВ
2.1. Графический метод определения вещественных корней
Вещественные корни представляют собой точки пересечения
графика полинома P(x) с горизонтальной осью. Графический
метод определения корней заключается в снятии значений
абсцисс точек пересечения графика и оси. Такой способ дает
большую погрешность, и в случае близости нескольких корней
очень сложно построить график в таком масштабе, чтобы эти
корни стали хорошо различимы.
8
6
4
2
x  4x 3
2
5
4
3
2
1
0
2
x
1
Графический метод определения вещественных корней
В случае корня кратности два график полинома не пересекает ось, а
касается её, поэтому снять значение корня с хорошей точностью
тяжело. Даже если при этом будет получено значение корня с
удовлетворительной точностью, то о кратности его ничего не будет
известно. Для локализации корня кратности два можно привлечь
график производной. Для производной этот корень будет простым,
следовательно, график производной пересекает ось. Точка
пересечения и определит значение кратного корня.
4
2
x  2x 1
2
2x 2
2
1.5
1
0.5
x
0
0.5
1
Графический метод определения вещественных корней
Корень более высокой кратности, чем 2, является кратным корнем и
первой производной. В этом случае график производной также
будет касаться оси и плохо поможет в определении значения
корня. Здесь можно использовать производную r–1 порядка,
которая содержит уже простой корень и пересекает ось, а не
касается её.
МЕТОДЫ ВЫЧИСЛЕНИЯ КОРНЕЙ ПОЛИНОМОВ
2.2. Сравнение погрешностей для простого и кратного корня
приближенного полинома
Исходя из математических выражений погрешностей корней,
погрешность кратного корня значительно больше погрешности
простого. Так, если для простого корня, к примеру, Δx=10–12, то для
корня кратности r получим Δx=10–6 при r = 2, Δx=10–3 при r = 4 и
т.д. Помимо резкой потери точности, кратные корни вносят
проблемы и методологического характера. Так, в ряде прикладных
задач имеет смысл рассматривать только вещественные корни.
При этом корень четной кратности может “пропасть” при сколь
угодно малом изменении коэффициентов полинома.
Например, полином
имеет кратный корень
.
2
P2 ( X )  x  2 x  1
,2  1
При округлении, например,
свободного члена до 1+ε x1(ε
>0), этот
корень превращается в пару комплексных корней вида:
и
, вещественных корней у полинома не остается.
x 1 i 
x 1 i 
МЕТОДЫ ВЫЧИСЛЕНИЯ КОРНЕЙ ПОЛИНОМОВ
2.3. Вычисление корней полиномов второй и третьей степени
Корни квадратного уравнения ax2+bx+c=0 находятся по известным
формулам:
 b  b 2  4ac
(7)
x1, 2 
2a
Однако эти формулы могут приводить к потере точности одного из
корней, которая связана с эффектом вычислительной ловушки
при вычитании близких чисел. Поэтому в случае вещественных
корней рекомендуется пользоваться формулами:

b  b 2  4ac
 x1   sign (b)

2a

2c
 x 2   sign (b)

b  b 2  4ac
(8)
Вычисление корней полиномов третьей степени
Для уравнения третьей степени вида y  py  q  0 также возможно
вычисление корней по известным формулам Кардано. К такому
виду может быть приведено любое кубическое уравнение
ax 3  bx 2  cx  d  0 при использовании следующей замены:
3
b
x y
3a
b2
c
p 2 
a
3a
2b 3
bc d
q


27a 3 3a 2 a
Сама формула Кардано имеет вид:
y3 
q
q


 
3   
2
108
2
108
где   27q 2  4 p 3 есть дискриминант многочлена y3 + py + q.
(9)
МЕТОДЫ ВЫЧИСЛЕНИЯ КОРНЕЙ ПОЛИНОМОВ
2.4. Уточнение корней полинома методом Ньютона
Уточнение действительных корней
Метод служит для уточнения корней, найденных другим способом,
например, графическим. Пусть xt – вещественный корень
полинома P(x), x0 – его приближенное значение. Поскольку
полином имеет непрерывные производные, в том числе и второго
порядка, его значение в окрестности точки x0 , можно представить
с помощью формулы Лагранжа в виде
P( x)  P( x 0 )  P ( x 0 )( x  x 0 ) 
1
P ( z )( x  x 0 ) 2
2
где z– некоторая точка, лежащая между x0 и x. В частности, если
положить x=xt, то с учетом P(xt)=0, получим для xt уравнение
P( x 0 )  P ( x 0 )( xt  x 0 ) 
1
P ( z )( xt  x 0 ) 2  0
2
Если xt–x0 мало, пренебрегая этим членом, получим приближенное
линейное уравнение. Обозначая его корень через x1, найдем
P ( x0 )
(10)
x x 
1
0
P( x0 )
Уточнение корней полинома методом Ньютона
Эта формула определяет одну итерацию в методе Ньютона. Метод
Ньютона называют также "методом касательных", что связано с
определенной графической интерпретацией. На рисунке ниже
изображена функция, нуль которой необходимо найти, и
касательная в точке очередного приближения. Можно увидеть, что
каждое последующее приближение xn1 лучше предыдущего .
Уточнение корней полинома методом Ньютона
Схема алгоритма:
Находим значение xn1 по формуле (10), которое служит начальным
приближением для следующей итерации метода Ньютона. При
первом прохождении алгоритма начальное приближение x0
необходимо задать вручную. Можно, например, вычислить его с
помощью графического метода.
Критерием
окончания
итераций
служит
близость
двух
последовательных значений. Проверка условия xn1  xn   после
каждого шага свидетельствует о том, что фактическая точность
последнего приближения еще выше. Если условие выполняется,
то xn+1 – искомый корень, останавливаем итерационный процесс.
Если нет, то берем xn+1
за начальное приближение для
следующей итерации и вновь выполняем шаг 1.
Метод Ньютона, не обладает неизбежной сходимостью. Поэтому
обычно контролируется число итераций. Если вторая производная
P (x) на отрезке (x0, xt) и при этом
не изменяет знака
x0 )  P(Ньютона
x0 )  0
тоP(метод
неизбежно сходится.
Уточнение корней полинома методом Ньютона
Уточнение комплексных корней
Метод Ньютона был рассмотрен применительно к случаю
вещественных корней, однако он применим и к уточнению
комплексных корней. Производимые операции абсолютно
аналогичны операциям с вещественными корнями.
МЕТОДЫ ВЫЧИСЛЕНИЯ КОРНЕЙ ПОЛИНОМОВ
2.5. Метод Берстоу уточнения квадратичного делителя
полинома
Используемая в методе Ньютона идея линеаризации, применяется
во многих других задачах вычислительной математики. Одним из
таких применений является метод Берстоу, служащий для
уточнения приближенного делителя полинома.
Вместо уточнения найденных комплексных корней можно уточнять
квадратичные делители, соответствующие сопряженным корням
R-факторизованной формы (6) полинома.
Основная идея метода заключается в следующем.
n
n 1
Разделим заданный полином Pn ( x)  a 0  x  a1  x    a n
на
квадратичный делитель с неопределенными коэффициентами
p и q: Q(x)=x2+px+q. В результате получим:
P( x)  Q( x) R( x)  Ax  B
(11)
Метод Берстоу уточнения
квадратичного делителя полинома
Коэффициенты остатка являются некоторыми, неизвестными пока,
функциями p и q: A = A(p, q), B = B(p, q). Для того, чтобы деление
P(x) на Q(x) осуществлялось нацело, необходимо, чтобы эти
функции обращались в ноль, т.е. задача нахождения Q(x) сводится
к решению системы уравнений:
(12)
 A( p, q)  0,

 B( p, q)  0.
МЕТОДЫ ВЫЧИСЛЕНИЯ КОРНЕЙ ПОЛИНОМОВ
2.6. Схема Горнера
Схемой Горнера называют схему деления полиномов для частного
случая, когда делителем является линейный полином Q=x - x1.
В общем случае операция деления полинома Р (делимое) на
полином Q (делитель) определяется как поиск такого полинома S
(частное) и такого полинома R (остаток), чтобы выполнялось
P  QS  R
условие:
(13)
Если остаток R равен нулю, то происходит деление нацело, т.е.
P=QS, при этом, степень частного S равна n – m, где n – степень
полинома P, а m – степень полинома Q, причем n >= m.
При делении полинома на линейный полином вида Q  x  x1 , получаем
простое рекуррентное соотношение для коэффициентов частного:
c n 1  a n ;
k=n-2, n-3,…0
(14)
c k  a k 1  c k 1 x,
где c0, c1,…, cn–1 являются коэффициентами частного, аn – делимого.
Схема Горнера
Соотношение (13) приобретает вид:
Pn ( x)  ( x  x1 ) S ( x)  c n
(15)
По следствию из теоремы Безу, если xi является корнем полинома, и
только в этом случае деление полинома P(x) на двучлен (x – xi)
осуществляется нацело.
Для пары комплексных сопряженных корней деление на Q  ( p  z )( p  z ) ,
где z=x+jy, проводится по следующей схеме:
r=2x; q= -x2 -y2; cn-2= an;
(16)
cn-3= an-1 +ran; cn= ak+2 +rck+1 +qck+2, k=n-4, n-5, …0
где с0, … сn-2 – коэффициенты полинома, полученного в результате
2
деления на ( p  z )( p  z )  p  rp  q .
Итак, схему Горнера можно использовать для нахождения корней
полинома. Данный алгоритм требует порядка 2n арифметических
операций (сложений и умножений), так что является довольно
экономичным.
Схема Горнера
Алгоритм.
1. Пусть zi – очередное приближение для корня полинома
f ( p)  a n p n  a n 1 p n 1    a0 , m – степень полинома. Построим
квадратичную аппроксимацию для значений
полинома в
2
 

 (z )
f
,
f
, fi
f
(
z


z
)

f

f


z

f
i
i
окрестности точки zi :
.
Здесь
–
i
i
i
i
2
значения полинома, его первой и второй производных в точке zi.
Следующее приближение для корня полинома определим в виде
zi 1  zi  zi 1 , где приращение z i 1 находим, решая квадратное
2

 (z i 1 )
0 .
уравнение f i  f i  zi1  f i
2
Из двух решений этого уравнения выберем наименьшее по модулю:
f
(17)
2 i
z i 1 
fi

2f  f
1 1 i i

( fi )2

Схема Горнера
z i 1
Если z ,то есть приращение на очередном шаге становится мало
i
по сравнению с zi, то принимаем текущее значение zi за
очередной, комплексный в общем случае, корень полинома
z=x+iy. Переходим к шагу 2. Если же поставленное условие не
выполняется, то повторяем текущий шаг, взяв zi равным zi+1
.
2. Если мнимая часть корня равна 0, т.е. z=x, то полученный корень –
вещественный. В этом случае включаем z в число корней и
переходим к шагу 3. Если же мнимая часть не равна нулю, то
z=x-iy также является корнем полинома. Включаем z и в число
z
корней и переходим к шагу 4.
3. Разделим исходный полином на (p-x), используя схему Горнера для
нахождения коэффициентов полинома, получающегося после
деления на линейный полином. Уменьшим m на 1. Переход к шагу
5.
4. Разделим исходный полином на (p-x-iy)(p-x+iy), используя схему
Горнера
для
нахождения
коэффициентов
полинома,
получающегося после деления на квадратичный полином.
Уменьшим m на 2. Переход к шагу 5.
Схема Горнера
5. Если степень полинома m стала равна 0, то заканчиваем
выполнение алгоритма, т.к. все корни были найдены. Если m>0, то
для выделения следующего корня или комплексной пары корней
применим итерационный процесс, описанный в шаге 1, к
полиному, полученному после деления по схеме Горнера.
Примечания:
1. Рассмотрим особые случаи, которые могут иметь место при
вычислении корней. Если fi не равна нулю в точке zi, первая
производная в ней обращается в ноль, а вторая – нет, то вместо
формулы (17) необходимо воспользоваться формулой:
f
(18)
z i 1   2 i
fi

2. Если fi не равна нулю в точке zi, а первая и вторая производные в
ней обращаются в ноль, то сделаем случайный шаг, то есть
присвоим некоторое случайное значение. Остановка процесса
поиска текущего корня производится в том случае, когда величина
очередного шага станет крайне мала по сравнению с величиной zi.
МЕТОДЫ ВЫЧИСЛЕНИЯ КОРНЕЙ ПОЛИНОМОВ
2.7. Метод Рыбакова вычисления всех вещественных корней
Рассмотрев графический метод нахождения вещественных корней,
можно убедиться, что этот метод позволяет найти все
вещественные корни полинома. Недостатком является невысокая
точность, а также необходимость больших затрат личного времени
в тех случаях, когда приходится иметь дело с полиномами
высокой степени. Однако можно избежать этих недостатков и
сделать этот метод полностью автоматическим.
В методе Л.М.Рыбакова шаг сканирования hк=хк+1–хк отрезка (xl, xr)
определяется
по
формуле,
напоминающей
формулу,
используемую в методе Ньютона:
P( xk )
(19)
xk 1  xk 
P
МЕТОДЫ ВЫЧИСЛЕНИЯ КОРНЕЙ ПОЛИНОМОВ
2.8. Метод сопровождающей матрицы
Можно доказать, что матрица
 a n1

 an
A 1

 
 0


an2
an
0
 

a1
an
0
0

1







0 
a0
an
0

(20)
называемая
сопровождающей матрицей для полинома
n
P( x)   ai x i , имеет собственные значения равные корням
i 0
полинома. Как известно, собственными значениями матрицы
называются такие числа λ, для которых выполняется равенство
Av  v (причем имеется ненулевое решение уравнения
( A  E )v  0 .
На сегодняшний день существуют некоторые весьма эффективные
методы поиска собственных значений матриц. Таким образом,
задачу поиска корней полинома можно свести к задаче поиска
собственных значений сопровождающей матрицы.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Загускин В.Л. Курс лекций «Полиномы». – Н. Новгород: Издательство
Нижегородской лаборатории программных технологий, 2000.
2. Загускин В.Л. Справочник по численным методам решения
алгебраических и трансцендентных уравнений. / Под редакцией А.М.
Лопшица. – М.: ФИЗМАТГИЗ, 1988.
3. Лапчик М.П. Численные методы. – М.: Издательский центр «Академия»,
2005.
4. Бахвалов Н.С. Численные методы. – М.: Высшая школа, 2002.
5. Корнюшин П.Н. Численные методы. – Владивосток: Издательство
Дальневосточного университета, 2002.
6. Удерман Э. Г. Метод корневого годографа в теории автоматических
систем. – М.: Наука, 1972.
7. Максимов Ю.А., Филлиповская Е.А. Алгоритмы решения задач
нелинейного программирования. — М.: МИФИ, 1982.
8. http://alglib.sources.ru/
9. http://ru.wikipedia.org/wiki
10. Рыбаков
Л.М.
Метод
последовательного
вычисления
всех
действительных корней уравнения. //Математическое просвещение. –
1961. №6. –с.262–263.