L_8
реклама

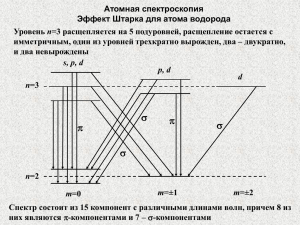
Атомная спектроскопия Эффект Штарка Эффект Штарка – расщепление уровней атома на ряд подуровней при помещении атома во внешнее электрическое поле Поправки к уровням энергии находятся при использовании теории возмущений в первом и втором порядках E (1) n Vnn , 2 E (2) n Vmn (0) , (0) m En Em Vij – матричные элементы возмущающего потенциала Оператор взаимодействия поля с атомом имеет вид: Hˆ ' ED ( Ez E) EDz D - дипольный момент атома E - напряженность электрического поля Атомная спектроскопия Эффект Штарка Матричные элементы оператора дипольного момента равны нулю. Поэтому 2 E f E 2 j f Dz j Ef Ej Выражение для отличных от нуля матричных элементов имеет вид: nJM Dz n ' J ' M J 2 M 2 , J ' J 1 nJM Dz n ' J ' M M , J ' J Отсюда: E E 2 A BM 2 Расщепление уровней пропорционально квадрату напряженности электрического поля - квадратичный эффект Штарка Расщепляются только те уровни, для которых проекция полного момента отлична от нуля Атомная спектроскопия Эффект Штарка Уровни с M=0 не расщепляются, а только испытывают сдвиг Снятие вырождения происходит частично, поскольку уровни с противоположными значениями M смещаются одинаково Расщепление пропорционально квадрату M -асимметричное Случай сильных полей или вырожденных состояний – линейный эффект Штарка Поправки к энергии состояний находятся из решения секулярного уравнения Vnm E (1) n δ nm 0 2 2 E nJ E 0 , 2 En ' J ' E0 . 2 Атомная спектроскопия Эффект Штарка H'' – оператор суммарного вклада электростатического и спин-орбитального взаимодействий Тогда: nJ H '' nJ , 2 n ' J ' H '' n ' J ' . 2 nJ Dz nJ E 2 nJ H '' nJ E nJ Dz n ' J ' E 2 nJ H '' n ' J ' 0 2 2 n ' J ' Dz nJ E n ' J ' H '' nJ n ' J ' Dz n ' J ' E n ' J ' H '' n ' J ' E nJ Dz nJ n ' J ' Dz n ' J ' 0 nJ H '' n ' J ' n ' J ' H '' nJ 0 Атомная спектроскопия Эффект Штарка E 2 nJ Dz n ' J ' E 2 n ' J ' Dz nJ E 2 E 2 0 2 Решение имеет вид: E1 =-E 2 = nJ Dz n ' J ' E 2 2 2 При отсутствии внешнего поля: E= 2 2 2 При условии: nJ Dz n ' J ' E 2 2 2 nJ Dz n ' J ' E1 E 2 E2 2 Атомная спектроскопия Эффект Штарка 2 2 При условии: nJ Dz n ' J ' E 2 2 2 E1 E 2 nJ Dz n ' J ' E линейный эффект Штарка E /2 /2 E Атомная спектроскопия Эффект Штарка. Частоты спектральных компонентов M 1 Наблюдение вдоль оси z - s-компоненты: ωσ ( M ) ω0 ( A A ') BM 2 B '( M 1) 2 E 2 Наблюдение в других направлениях - s-компоненты и p-компоненты: ωπ (M ) ω0 ( A A ') ( B B ') E M=±1 M=0 J=1 s p J=2 M 0 2 s p s M=±2 M=±1 M=0 Атомная спектроскопия Эффект Штарка для атома водорода Вследствие вырождения энергетических состояний даже в сколь угодно слабых полях эффект Штарка всегда линеен Расщепление состояний при n=2 (l=0, m=0; l=1, m=0,±1) 00 Dz 0 1 00 Dz 11 0; 00 Dz 10 0 для m=±1 для m=0 E1 E 1 0 E 0 00 Dz 10 E 0 10 Dz 00 E E 0 E E 00 Dz 10 E (1) 0 (2) 0 Состояние n=2 расщепляется на три подуровня. Один из них двукратно вырожден, а два других расщеплены симметрично в противоположных по энергиям направлениях Атомная спектроскопия Эффект Штарка для атома водорода Расщепление состояний при n=3 (l=0, m=0; l=1, m=0,±1; l=2, m=0,±1 ,±2) Имеем 4 отличных от нуля матричных элемента: 11 Dz 21 ; 00 Dz 10 ; 10 Dz 20 ; 1 1 Dz 2 1 для m=±2 для m=±1 E 2 E 2 0 E m 1m Dz 2m E 0 2m Dz 1m E E m E1 E-1 1m Dz 2m E для m=0 E 0 00 Dz 10 E 0 10 Dz 00 E E 0 10 Dz 20 E 0 0 20 Dz 10 E E 0 E 0 0; E 0(1) E (2) E 0 2 00 Dz 10 10 Dz 20 2