Основные результаты выполнения проекта

ЗАДАЧИ ВЫСОКОСКОРОСТНОГО СОУДАРЕНИЯ НЕЛИНЕЙНО-УПРУГИХ ТЕЛ
О.В. Дудко, Ю.Е. Иванова, А.А. Лаптева, А.А. Манцыбора, Д.А. Потянихин, В.Е. Рагозина, М.М. Русанов
Федеральное государственное бюджетное учреждение науки Институт автоматики и процессов управления Дальневосточного
отделения Российской академии наук
Проект РФФИ № 11-01-98514-р_восток_а
Введение
Задачи о соударении упругих и упругопластических тел являются предметом многочисленных теоретических и экспериментальных исследований.
Вопросы современного машиностроения, связанные с конструированием подводных и космических аппаратов, нефте- и газопроводов, быстроходных
машин и механизмов, заставляют исследователей все глубже проникать во внутренние закономерности процесса удара, потому что ошибки при
проектировании таких высокотехнологичных объектов крайне нежелательны. Помимо уровня деформаций и напряжений, конструкторам необходимы
сведения о поверхностях разрывов, вызываемых производимым ударом. В зависимости от возможности существования волн разгрузки и от
интенсивностей разрывов на волновых поверхностях необходимо выбирать материалы, способные адекватно реагировать на оказываемые возмущения,
продлевая тем самым срок службы корпусов и механизмов. Настоящий проект направлен на постановку и решение ряда задач о соударении твердых
тел, обсуждение возникающих при этом комбинаций волновых поверхностей и вопросов единственности решения таких задач. Результаты исследования
процессов, происходящих при контактных взаимодействиях твердых тел, представляют несомненный интерес как с фундаментальной, так и с
прикладной точки зрения.
Основные результаты
Плоские автомодельные задачи динамики нелинейно-упругой и упругопластической сред.
Критерии единственности решения
Любое динамическое воздействие на твердое тело неизменно сопровождается нагреванием материала, поэтому полная система модельных
соотношений динамики деформирования содержит закон теплопроводности. Однако в сплошной среде тепло распространяется существенно
медленнее ударных волн – передних фронтов продвижения граничных возмущений. Пренебрежение тепловыми эффектами (адиабатическое
приближение) – естественный логический шаг при изучении волн деформаций в твердых телах, который приводит в автомодельных задачах упругого
деформирования к неединственности их решения. На этапе постановки краевой задачи невозможно определить характер возникающих волновых
фронтов (ударные волны или простые волны Римана). Для разрешения этой проблемы в проекте предложены методики выбора единственной волновой
картины из числа математически допустимых вариантов путем проверки термодинамического условия совместности разрывов и условия
эволюционности ударных волн непосредственно во время численного счета. Для описания механических свойств деформируемой нелинейно-упругой
среды выбрана пятиконстантная нелинейная модель (материал Мурнагана), упругопластическая среда рассматривалась в рамках модели больших
упругопластических деформаций. Разработанные алгоритмы численного счета основаны на неявных конечноразностных схемах и методе пристрелки по
параметру. Построены решения плоских автомодельных задач о высокоскоростном соударении нелинейно-упругих, упругопластических тел с плоскими
непараллельными границами, о внедрении тонкого жесткого клина в нелинейно-упругую среду, о движении ступенчатой нагрузки по границе
упругопластического полупространства, о снятии нагрузки с границы упругопластического полупространства.
Высокоскоростное соударение двух тел с плоскими
непараллельными границами
S4
G3n (3)
S3
G4n
(4)
5
+
3
G n
v 20
3
v10
b4
b3
L
v0
GLn
S
b1
G2n
S4
G3n (3)
S3
0
(2)
S1
G1n (1)
b
2
GLn ( L )
b
2
+
2
S
b1
q  [q ,q ]
2
1
+
2
G n
0
(2 + )
S1
G n
G1n
I
b3-
L
x1
G1n (1)
x2
G2
G4n (4)
b3+
b
2
b
q  [q ,q ]
2
v10
v0
0
(2 + )
S1
pij  const
0

2
+
2
 G
+
2


+
1

1 1

S
x2
pij  const
1
x1
+
1
G
+
1
x1

0
21

L1
S
b1
G1n (1)
x2
S
21
L2
O
1
+
2
nn  n  0
v 20
G2- n (2 - )
+
2
+
1
f (ij )  k
5
II
bL
2

11
(3 - )
+
2
1
I
x1
G
0
b4
G n
(1)
S4
3
x2
0
4
3
GLn ( L )
G2- n (2 - )
+
2
3

L1
L1
S
(2)
q  [q ,q ]
+
3
L2
O

O
1
G3+ n (3+ )
v0
0
S1
G2n
f (ij )  k
nn  n  0
L2
v0
b1
2
5
v 20
v10
b2
S1
v10
bL
+
3
bL
S2
II
b4
b
x1
G4n (4)
b3
L
L
v 20
(3 - )
b4
b3-
x2
5
II
3
I
4
3
G n
GLn ( L )
1
S2
L1
G4n (4)
4

b2
( L)
3
3
L2
O
bL
2
q  [q ,q ]
+
3
II
4
(3 + )
S4
Динамика разгрузки упругопластического
полупространства
I
x1
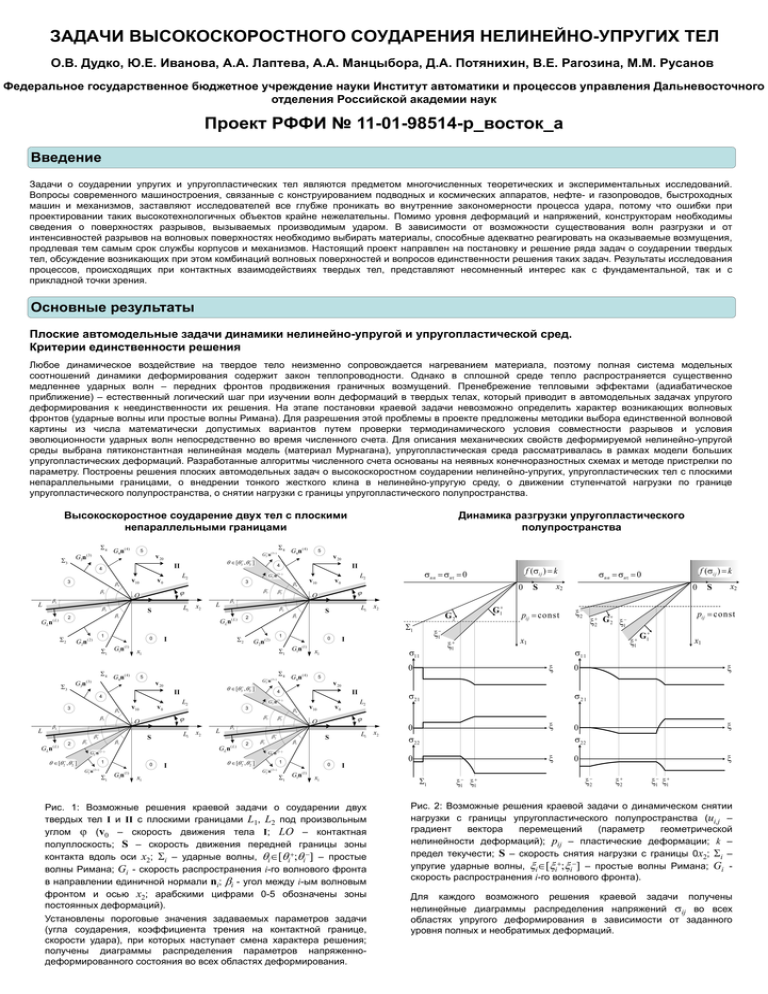
Рис. 1: Возможные решения краевой задачи о соударении двух
твердых тел I и II с плоскими границами L1, L2 под произвольным
углом  (v0 – скорость движения тела I; LO – контактная
полуплоскость; S – скорость движения передней границы зоны
контакта вдоль оси x2; Si – ударные волны, qi[qi+;qi-] – простые
волны Римана; Gi - скорость распространения i-го волнового фронта
в направлении единичной нормали ni; bi - угол между i-ым волновым
фронтом и осью x2; арабскими цифрами 0-5 обозначены зоны
постоянных деформаций).
Установлены пороговые значения задаваемых параметров задачи
(угла соударения, коэффициента трения на контактной границе,
скорости удара), при которых наступает смена характера решения;
получены диаграммы распределения параметров напряженнодеформированного состояния во всех областях деформирования.
x2

0
22

0
S1
1

+
1


0
22

0
-2
+2
1- 1+
Рис. 2: Возможные решения краевой задачи о динамическом снятии
нагрузки с границы упругопластического полупространства (ui,j –
градиент
вектора
перемещений
(параметр
геометрической
нелинейности деформаций); pij – пластические деформации; k –
предел текучести; S – скорость снятия нагрузки с границы 0x2; Si –
упругие ударные волны, i[i+;i-] – простые волны Римана; Gi скорость распространения i-го волнового фронта).
Для каждого возможного решения краевой задачи получены
нелинейные диаграммы распределения напряжений ij во всех
областях упругого деформирования в зависимости от заданного
уровня полных и необратимых деформаций.
Особенности распространения и взаимодействия волн деформаций при дополнительных ограничениях,
накладываемых на механические свойства материалов, геометрию и характеристики волновых фронтов
Нестационарная задача плоской деформации массива
нелинейно-упругой среды с границей ненулевой кривизны
С целью исследования процесса распространения возмущений при
ударном нагружении криволинейной границы нелинейно-упругого
полупространства
предложено
обобщение
метода
построения
приближенных
решений
краевых
задач
динамики
ударного
деформирования в виде лучевых разложений для двумерного случая
плоской деформации. Метод лучевых рядов, получивший широкое
распространение при изучении различных динамических процессов, в
случае нестационарного деформирования применяется в окрестности
передних волновых фронтов с выбором коэффициентов лучевых рядов
в виде разрывов частных производных от искомых функций. До
настоящего времени модификации лучевого метода были построены
для простейших задач одномерного типа, изменение лучевого метода
для описания ударных волн путем построения внутренних
дополнительных рядов специального вида проведено для наиболее
простой задачи о плоской продольной ударной волне. Решение задачи
плоской деформации массива нелинейно-упругой среды с границей
ненулевой кривизны позволяет для двух ударных волн изучить вопросы
работы с несколькими лучевыми сетками. Для каждой ударной волны в
окрестности ее волнового фронта решение определяется на основе
лучевых координат, согласованных с данной волной. Учтены факторы
расходимости лучевых координат, связи геометрии этих координат и
поля деформаций. Предложенные методы приближенного описания
лучевой геометрии, установления взаимосвязи между несколькими
лучевыми сетками, а также между лучевой сеткой и подвижной границей
могут быть перенесены на задачи ударного деформирования более
общего вида, не связанные предположением о плоском характере
деформации, а также на краевые задачи динамики сред с
усложненными механическими свойствами.
Одномерное взаимодействие двух идущих навстречу друг
другу плоских сдвиговых ударных волн, поляризованных
в различных плоскостях
В общем случае нестационарная динамика деформирования твердых тел
изучает нелинейные эффекты возникновения и распространения
поверхностей сильных разрывов – ударных волн, на которых процессы
деформаций изменения формы и объема оказываются взаимозависимыми,
а разрывы – комбинированными. Если основным интересом исследований
являются закономерности распространения по среде сдвиговых
деформаций, то естественным ограничением на механические свойства
материала является запрет изменения объема (т.е. среду полагают
несжимаемой). Такое упрощающее предположение позволило провести
анализ особенностей взаимодействия ударных волн на примере решения
краевой задачи о столкновении двух плоских одномерных ударных волн
сдвиговой нагрузки с различной поляризацией. Построенные обобщенные
решения демонстрируют возможность возникновения в результате такого
взаимодействия различных отраженных волновых картин из ударных и
простых волн. Указаны критерии, согласно которым можно уже на
постановочном этапе, исходя из параметров идущих навстречу ударных
волн сдвиговой нагрузки (их интенсивности и поляризации), определить
характер отраженных волновых фронтов.
1
-H1
1
G1
0
0
G2
x3
2
x2
0:
0
I
e2
y
z
0 e1
G1
x1
l μ sm
ν
n
L(t ) t 0
L(t ) t 0 S 2
II G 2
I:
II:
(0)
i
0
(0)
i, j
0
u
u
u  u ( x1 , x2 , t )
(I)
i
u
u
(II)
i
3
x3

a0t 
u |r  r0 () +  v0t +
e1 , t  0, v 0 , a0 - const

2 

S1 - продольная ударная волна со скоростью G1:
[ui , j ]|S1 ni n j  1  0, [ui , j ]|S1 mi n j  1  0
( y, s ) - лучевые координаты на S1
S 2 - квазипоперечная ударная волна со скоростью G2:
[ui , j ]|S2 i  j  2  0, [ui , j ]|S2 i  j   2  0, 2   2
( z, l ) - лучевые координаты на S 2
(2)
2,1
1
(i 1,2)
2
x2
5
0
x3
0
S2
(2)
3,1
G3
+
G4
4
G6
2
G5
S3
4
x2
S6
S5
H2
x1
| s1 || s5 || s 2 |, s5  s1 + s 2
-H1
G3
G4
4
G6
2
G5
2
S3
S4
x2
S6
S5
H2
x1
| s1 || s 2 || s5 |, s5  s1 + s 2
1
-H1
5
2
3
H2
1
( x1 , x2 , t )
Рис. 3: Движение криволинейной границы L(t) нелинейноупругого полупространства по закону
i i 1, i i  0,
(1)
3,1
(i 1,2)
(II)
i
S1
1
s1 {u ;u }, s2 {u ;u }
(1)
2,1
(I)
i
S1
ni ni 1, mi ni  0,
2
x1
1
1
3
x3
0
-H1
G3
+
G4
5
+
6
4
G
2
G5
2
S3
4
x2
6
S5
H2
x1
| s5 || s1 || s 2 |, s5  s1 + s 2
Рис. 4: Отраженные волновые картины, возникающие внутри
несжимаемого нелинейно-упругого слоя [-H1;H2] в результате
взаимодействия двух ударных волн сдвиговой нагрузки S1, S2 (Si –
упругие ударные волны, i – простые волны Римана; Gi - скорость
распространения i-го волнового фронта; sj – вектор сдвига в j-й
зоне постоянных деформаций, j=0,1…5).
Основные публикации
1. Буренин А.А., Дудко О.В., Потянихин Д.А. О соударении двух упругих тел с плоскими границами // Вычислительная механика сплошных сред = Computational continuum mechanics,
2013. Т. 6. № 2. С. 157-167. ISSN 1999-6691.
2. Манцыбора А.А., Русанов М.М. Автомодельная задача о динамике разгрузки упругопластического полупространства // Сибирский журнал индустриальной математики. 2013.
Новосибирск: Изд-во Института математики им. С.Л. Соболева СО РАН. Т. XVI. № 2(54). С. 122-129. ISSN 1560-7518.
3. Буренин А.А., Дудко О.В., Лаптева А.А. К закономерностям распространения деформаций изменения формы // Сибирский журнал индустриальной математики. Новосибирск: Изд-во
Института математики им. С.Л. Соболева СО РАН. 2011. № 4. С. 14-23. ISSN 1560-7518.
4. Потянихин Д.А., Дудко О.В. К выбору физически обоснованных решений автомодельных краевых задач нелинейной динамической теории упругости // Вестник Нижегородского
университета им. Н.И. Лобачевского, 2011. № 4 (5). C. 2440–2442. ISSN 1993-1778.
5. Дудко О.В., Лаптева А.А. Распространение сдвиговых деформаций при не одномерном соударении двух плоских ортогонально поляризованных ударных волн нагрузки // Материалы
IX Международной конференции по неравновесным процессам в соплах и струях (NPNJ 2012), 25-31 мая 2012 г., Алушта. М.: Издательство МАИ, 2012. С. 360-361. ISBN 978-5-43160063-0.
6. Дудко О.В., Потянихин Д.А. Задача об отражении плоской продольной ударной волны от свободной границы // XXXVI Дальневосточная математическая школа-семинар имени
академика Е.В. Золотова, 4 – 10 сентября 2012 г., Владивосток : сборник материалов. (Электронный ресурс). Владивосток: ИАПУ ДВО РАН, 2012. С. 119-124. ISBN 978-5-7442-1517-0.
7. Русанов М.М., Манцыбора А.А. Задача разгрузки упругопластического полупространства // XXXVI Дальневосточная математическая школа-семинар имени академика Е.В. Золотова, 4
– 10 сентября. 2012 г., Владивосток: сборник материалов. (Электронный ресурс). Владивосток: ИАПУ ДВО РАН, 2012. С. 200-205. ISBN 978-5-7442-1517-0.
8. Потянихин Д.А. Высокоскоростное внедрение тонкого жесткого клина в упругую среду // Материалы XVII Международной конференции по вычислительной механике и современным
прикладным программным системам (ВМСППС 2011), 25–31 мая 2011 г., Алушта. М.: Изд-во МАИ-ПРИНТ, 2011. С. 397–400.
9. В.Е. Рагозина, Ю.Е. Иванова. О применении лучевых рядов в динамических задачах плоской деформации, обусловленной ударной нагрузкой // Известия Российской академии наук.
Механика твердого тела. 2013. (в печати).