Численное исследование резонансного радиального переноса быстрых ионов в газодинамической ловушке

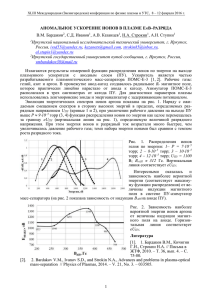
Численное исследование
резонансного радиального
переноса быстрых ионов в
газодинамической ловушке
Е.Ю.Колесников, Ю.А.Цидулко
Содержание
•
•
•
•
Постановка задачи
Модель и приближения
Результаты численных экспериментов
Выводы
В ходе экспериментов на ГДЛ
было обнаружено, что
радиальный профиль
распределения плотности
быстрых ионов уже, чем это
можно было бы ожидать
исходя из инжекции.
Формирование такого
профиля происходит за
время много меньшее
характерного времени
столкновений быстрых
ионов. Эксперименты также
показали отсутствие потерь,
которые могли быть
причиной формирования
подобного профиля.
Особенности ГДЛ
Важные особенности ГДЛ – высокое β и большой по
сравнению в радиусом плазмы ларморовский радиус
быстрых ионов.
Это приводит к тому, что становятся сравнимы частоты
азимутальных и баунс-колебаний:
VB V
 ~
~ 2
aB
a
V
b ~
L

a
 ~
a L
В отличии от ловушек с продольным током, резонансы не
являются следствием винтового характера силовых линий.
Постановка задачи
Наличие радиального переноса свидетельствует о нарушении
аксиальной симметрии.
Какова должна быть степень аксиальной
асимметрии, чтобы возник существенный перенос?
•
•
•
•
•
Приближения:
движение быстрых ионов бесстолкновительное,
магнитный момент сохраняется,
магнитном поле параксиальное.
Два этапа решения:
нахождение возмущения поля, создаваемое быстрыми ионами при
движении в аксиально-симметричном поле,
Рассмотрение движения тестовых частиц в возмущенном поле.
Движение в аксиальносимметричном поле
Запишем кинетическое уравнение для быстрых ионов:
df f d f
f


 Vz
 S,
dt t dt 
z
где источник ведущих центров быстрых ионов выберем в виде:
S
m 
 [J  J
m  
0
] [    0 ] [ ]S m exp[ m(   m )]
Стационарное решение кинетического уравнения будет
иметь вид:

n[ z , p] 

 d z  dE S



[ z , E , p]Dm [ z , z , E , p]  S  [ z , E , p]D m [ z , z , E , p]
Движение в аксиальносимметричном поле
где
Dm [ z , z , E , p ] 
[ z, E , p] 

1
cos[ m [ z ]] 

[ z, E , p][ z, E , p] sign[ z  z ]e im [ z ]  e im [ z ]  2i
2
tan[ mq] 

1

Vz [ z, E ]
1
2( E  B[ p, z ])
и

i
q

 m 
Знак τ задает направление обхода для правила Ландау
Роль резонансов
Неосесимметричное возмущение само по себе не может привести к
радиальному дрейфу, т.к. оно быстро исчезнет по причине фазового
размешивания при движении частиц, даже при слабом затухании.
Это обусловлено тем, что частицы на разных радиусах вращаются
с разной угловой скоростью.
Однако, высокое бета в ГДЛ позволяет реализоваться другому
режиму движения частиц – резонансному.
 M
 ,
 N
Где ωθ – частота баунс колебаний, ωφ – частота азимутальных
колебаний, а N и M – целые числа. При этом траектория
замкнута, и частица возвращается в те же точки на сечении
Пуанкаре. Фазового размешивания на резонансных
радиусах не происходит.
Нерезонансное движение
Резонансное движение
Возмущение магнитного поля
Поскольку основной вклад в несимметричное возмущение
плотности дают окрестности резонансных поверхностей,
возмущение магнитного поля удается записать в виде:
B  4 n f   hm,l K m,l [r /  ]Dm,l [ z ] cos[ m(   m )]
m ,l
Здесь Кm,l – ядро оператора двукратного усреднения по
площади ларморовской орбиты.
Возмущение магнитного поля
Динамика пробных частиц
Движение иона в магнитном поле, возмущаемом быстрыми
ионами описывается гамильтонианом:
2
mVz
H
  ( B  B),
2
где возмущение поля:
B  4n f
Черта - усреднение по площади ларморовской орбиты.
Гамильтониан записан в потоковых координатах ведущего
центра.
Численные эксперименты
Путем численного решения уравнений Гамильтона для
различных амплитуд неосесимметричного возмущения, были
получены следующие результаты.
B
B
 2 10
3
B
B
 7 10
3
B
B
 0 .2
Зависимость радиального переноса от времени для различных
значений δB/B
Выводы
• Для возникновения существенного резонансного переноса
быстрых ионов необходимо аксиально-несимметричное
возмущение их плотности на уровне 3%.
• Аксиально-несимметричное возмущение обусловленное
несимметричностью инжекции является недостаточным для
возникновения переноса.
Фазовое размешивание
Неосесимметричное возмущение само по себе не
может привести к радиальному дрейфу, т.к. оно
быстро исчезнет по причине фазового размешивания
при движении частиц, даже при слабом затухании.
Это обусловлено тем, что частицы на разных
радиусах вращаются с разной угловой скоростью.
Фазовое размешивание
Резонансы
Фазового
размешивания
на резонансных
радиусах не
происходит и
возмущение
сохраняется.
Перенос, δB/B=7*10-3
Перенос, δB/B=0,2
B
B
B
B
B
 2 10
3
 4 10
3
 7 10
B
B
3
B
B
2
 6 10
B
 0,2
r

 r 
 
  
2
x
y