ОГЭ 2015 1 вариант Часть 1 Модуль «Алгебра»
реклама
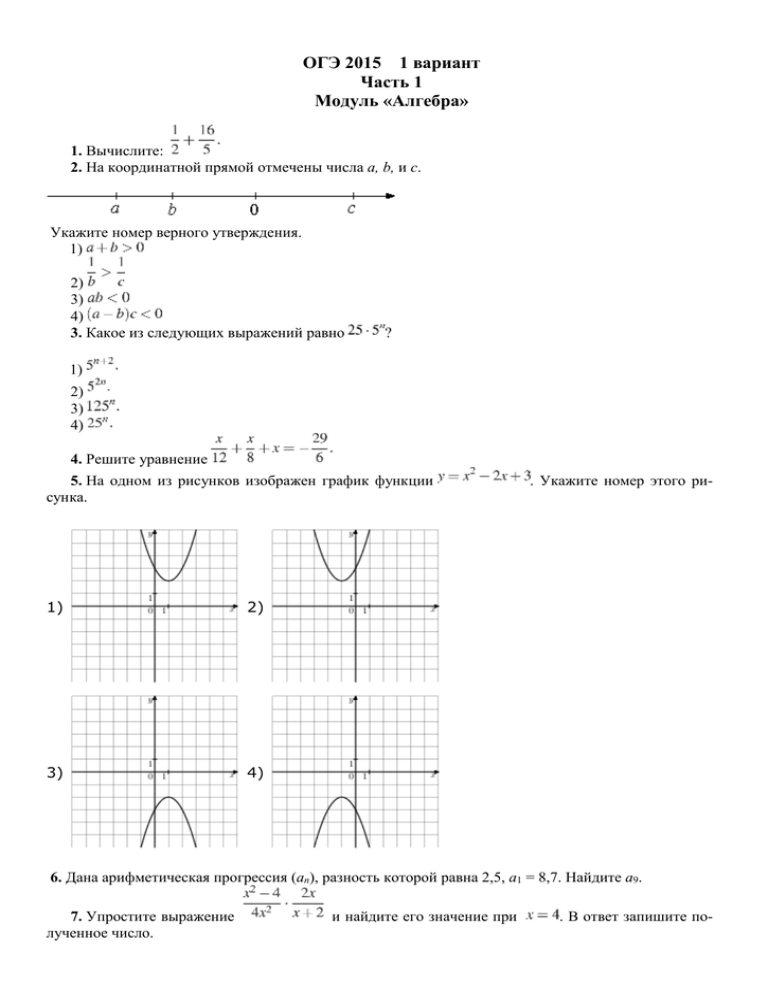
ОГЭ 2015 1 вариант Часть 1 Модуль «Алгебра» 1. Вычислите: 2. На координатной прямой отмечены числа a, b, и c. Укажите номер верного утверждения. 1) 2) 3) 4) 3. Какое из следующих выражений равно ? 1) 2) 3) 4) 4. Решите уравнение 5. На одном из рисунков изображен график функции сунка. 1) 2) 3) 4) . Укажите номер этого ри- 6. Дана арифметическая прогрессия (an), разность которой равна 2,5, a1 = 8,7. Найдите a9. 7. Упростите выражение лученное число. и найдите его значение при . В ответ запишите по- 8. Решите неравенство 1) (− ∞; 8) 2) (− ∞; 1) 3) (8; +∞) 4) (1; +∞) Модуль «Геометрия» 9. Биссектрисы углов B и C треугольника ABC пересекаются в точке K. Най дите , если ,а 10. Радиус окружности с центром в точке O равен 65, длина хорды AB равна 126 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k. 11. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 30°. Найдите площадь треугольника. 12. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В иС. Найдите расстоя- ние от точки А до прямой BC. Ответ выразите в сантиметрах. 13. Какие из следующих утверждений верны? 1) Любые два прямоугольных треугольника подобны. 2) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8. 3) Стороны треугольника пропорциональны косинусам противолежащих углов. 4) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними. Если утверждений несколько, запишите их через точку с запятой в порядке возрастания. Модуль «Реальная математика» 14. В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России с 1 сентября 2013 года. Превышение скорости, км/ч 21—40 41—60 61—80 81 и более Размер штрафа, руб. 500 1000 2000 5000 Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 90 км/ч на участке дороги с максимальной разрешённой скоростью 40 км/ч? 1) 500 рублей 2) 1000 рублей 3) 2000 рублей 4) 5000 рублей 15. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления (в мм рт. ст.) во вторник в 12 часов дня. 16. В городе 190 000 жителей, причем 29% – это пенсионеры. Сколько примерно человек составляет эта категория жителей? Ответ округлите до тысяч. 17. На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 4 м? 18. На диаграмме показано количество MS, присланных слушателями за каждый час четырёхчасового эфира программы по заявкам на радио. Определите, на сколько больше сообщений было прислано за последние два часа программы по сравнению с первыми двумя часами этой программы. 19. У бабушки 20 чашек: 5 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами. Часть 2 Модуль «Алгебра» 20. Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, гдеI — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 588 ватт, а сила тока равна 7 амперам. 21. Сократите дробь 22. Чтобы накачать в бак 117 л воды, требуется на 5 минут больше времени, чем на то, чтобы выкачать из него 96 л воды. За одну минуту можно выкачать на 3 л воды больше, чем накачать. Сколько литров воды накачивается в бак за минуту? 23. Постройте график функции и найдите все значения при которых прямая имеет с графиком данной функции ровно одну общую точку. Модуль «Геометрия» 24. В треугольнике угол равен 56°, угол ной около этого треугольника окружности. равен 64°, . Найдите радиус описан- 25. В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что треугольники BEF и DFE равны. 26. На стороне BC остроугольного треугольника ABC (AB ≠ AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD = 27, MD = 18, H — точка пересечения высот треугольника ABC. Найдите AH.
