Расчёт сооружений С Ч I
реклама

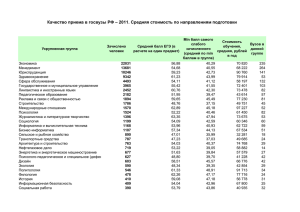
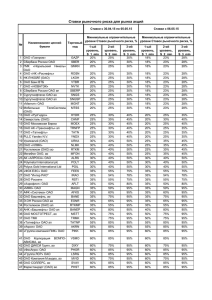
СТРОИТЕЛЬНАЯ МЕХАНИКА. Часть I Расчёт сооружений на действие подвижных и других временных нагрузок ТЕОРИЯ ЛИНИЙ ВЛИЯНИЯ 3 Определение силовых факторов с помощью линий влияния Определение с помощью линии влияния значения силового фактора от заданной нагрузки называется загружением линии влияния. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ НЕПОДВИЖНЫМИ НАГРУЗКАМИ 1. Сосредоточенная нагрузка F F yF Л.В. S SF = F* yF ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ НЕПОДВИЖНЫМИ НАГРУЗКАМИ 2. Сосредоточенный момент М F F = M/dx M k SM = SF + SFr = l = (–F)* yF + F* (yF +dy) = k dx dy yF yF + dy Л.В. S = F* dy = (M/dx)* dy = = M* dy/dx = M* tgaM aM SM = M* tgaM ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ НЕПОДВИЖНЫМИ НАГРУЗКАМИ 3. Распределённая нагрузка q x Sq dSq q ( x ) y ( x ) dx a x q(x) а dSq = dF* y(x) = = q(x) * y (x) * dx; dx q(x) dF=q(x) * dx y(x) wS Л.В. S При q(x) = const = q: Sq = q * w S ω S y ( x ) dx a ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ НЕПОДВИЖНЫМИ НАГРУЗКАМИ Формула загружения л.в. S: S = S F* yF + S M* tg aM + S q* wS Правило знаков: F>0 M>0 q>0 aM > 0 Л.В. S yF > 0 wS > 0 ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ НЕПОДВИЖНЫМИ НАГРУЗКАМИ Использование статически эквивалентных преобразований нагрузок Статически эквивалентное преобразование – замена группы сил другой группой, имеющей такие же главный вектор и главный момент (такую же равнодействующую), как и исходная. Правило: загружение прямолинейного участка линии влияния любыми статически эквивалентными нагрузками даёт один и тот же результат. a F1 F2 R F1 F2 F2 c a F1 F2 c y yR 2 F2 y1 yR y1 c ( y2 y1) y1 ( y2 y1) a F1 F2 Fy F y Л.В. S 1 1 2 2 F1 F2 SF1 F2 F1 y1 F2 y2 Fy F y SR SF1 F2 SR R yR (F1 F2) 1 1 2 2 F1 y1 F2 y2 F1 F2 R ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ НЕПОДВИЖНЫМИ НАГРУЗКАМИ Использование статически эквивалентных преобразований нагрузок Статически эквивалентное преобразование – замена группы сил другой группой, имеющей такие же главный вектор и главный момент (такую же равнодействующую), как и исходная. Правило: загружение прямолинейного участка линии влияния любыми статически эквивалентными нагрузками даёт один и тот же результат. a F qF F FFF q F1 y1 R c F2 yR y2 R1 = F R2 = 2(F + qb) R1 Ri = qli Rn = 3F yR1 Л.В. S b b li R2 yR2 n Ri yRi Л.В. S S Ri yRi i 1 SF1 F2 F1 y1 F2 y2 Fy F y SR R yR (F1 F2) 1 1 2 2 F1 y1 F2 y2 F1 F2 d d Rn yRn SR SF1 F2 ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ x q Л.В. S S(x) Smax Smin x Условие экстремума: dS ( x ) 0 dx Smax Smin ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ Условия максимума и минимума кусочной функции S(x) Условие максимума: S(x) Случай 1 Smax dS ( x ) > 0 при x = x0 –dx x dx < 0 при x = x0 +dx x0 dS ( x ) 0 ( x ( x0 x* ) dx ) S(x) Случай 2 > 0 при x = x –dx Smax x x 0 x* S(x) 0 dS ( x ) dx = 0 при x0< x < x* Случай 1 Случай 2 Smin x 0 x* x dx 0 ( x ( x0 x* ) dx ) < 0 при x = x* + dx Условие минимума: dS ( x ) 0 ( x ( x0 x* ) dx ) dx 0 ( x ( x0 x* ) dx ) ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 1. Сосредоточенная подвижная нагрузка F x F yF (x) yF,min yF,max Л.В. S SF,max = F* yF,max SF,min = F* yF,min ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 2. Подвижная полоса распределённой нагрузки q x q wS (x) а Л.В. S x Sq,max = q* wS,max Sq,min = q* wS,min wS ,max max wS ( x) max x x wS ,min min wS ( x) min x x y () d xa x y () d xa ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 3. Распределённая нагрузка q с произвольными разрывами q q q Л.В. S Загружение на Smax Загружение на Smin q q q q q Sq,max = q* wS,max = q* SwS+ Sq,min = q* wS,min = q* SwS– ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов x F1 F2 … Fn a1 a2 … Полигональная Л.В. S S(x) = S Fi * yFi (x) Smax Smin x ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов x dx F1F1 F2F… FnFn Fi F… 2… i … a1 a1 a2 a2 …… dx yFi yF2 ai yFi + dyFi dyFi dyFi yFn dx yF1 Полигональная Л.В. S S(x) + dS(x) S(x) = S [FFi i**y(FiyFi + dyFi )] ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов dS(x) = S [Fi * ( yFi + dyFi )] – S Fi * yFi = ai dyFi = dx * tg ai dyFi dx S Fi * dyFi dS(x) = dx * S(Fi* tg ai ) dS ( x ) ( Fi tg a i ) dx ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов xcr F1 F2 …Fcr … Fn Полигональная Л.В. S Груз, при расположении которого над вершиной линии влияния фактора S значение S от действия системы параллельных сосредоточенных грузов становится экстремальным ( Smax или Smin ), называется критическим грузом. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов x xcr F21 … F2…… F1 F FcrF… n Fn Fl SFr Л.В. S – треугольная Частный случайSполигональной ув al ar tg al = yв /a tg ar = – yв / b a b l ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов xcr = xcr – dx : F1 F2…Fcr …Fn dS(x) = (SF +F ) * tg a + l cr l dx + SFr * tg ar = SFl tg al = yв /a al dx При x = yв * [(SFl + Fcr ) /a – – SFr /b], SFr ув a ar b l dS(x) > 0 tg ar = – yв / b ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов xcr F1 F2 …Fcr …Fn SFl tg al = yв /a dx SFr ув dx al a = xcr + dx : dS(x) = SFl * tg al + + ( Fcr + SFr ) * tg ar = = yв * [SFl /a – – (Fcr + SFr )/b], ar b l При x dS(x) < 0 tg ar = – yв / b ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов Критерий определения критического груза в случае треугольной линии влияния a F F l l a F F F l cr l Графическая интерпретация критерия F1 F2 … … Fn F1 F2 Fcr Fn ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов Критерий определения критического груза в случае треугольной линии влияния a F F l l a F F F l cr l Графическая интерпретация критерия F1 F2 … … Fn Fn Fcr F2 F1 ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов Критерий определения критического груза в случае треугольной линии влияния a F F l l a F F F l cr l Критерий можно применить: F1 F2 … … Fn Критерий неприменим: F1 F2 Fn tg αl Fn Fcr F2 F1 Матрицы влияния Задача: определить силовые факторы S1 , S2 ,…, Si ,…, Sn от нагрузки, F1 A состоящей из сосредоточенных сил F1 , F2 ,…, Fj ,…, Fm . F2 Fj Например, S1= RA , S2 = Q1 , Si = M2 , Sn = MB Определение Si с помощью линии влияния: m 1 2 Fm F1 Si Fj y ji yji F2 j 1 y2i B В матричной форме: Si = [ y1i y2i …yji …ymi ]* Fj lSi Л.В. Si ymi S = l *F матрица (строка) влияния Fm i Si (M ) y1i силового фактора Si Все искомые силовые факторы: 2 yj2 S = L S* F = y12 y22 Л.В. S2 ym2 ( Q1 ) Матрица влияния силовых факторов – это матрица, строки которой состоят из ординат линий влияния искомых силовых факторов в точках приложения сосредоточенных нагрузок. F матрица ( вектор ) нагрузок λ S1 F1 y11 y21 y j1 ym1 F1 λ S2 F2 y12 y22 y j2 ym2 F2 F F λ Si y1i y2i y ji ymi j j λ Sn Fm y1n y2n y jn ymn Fm влияния LS LS матрица силовых факторов S (nxm) Матрицы влияния Общий случай загружения ( сосредоточенные и распределённые, силовые и моментные нагрузки ) F2 F1 Fj y q F1y A F2y Fjy qy A qx F2x M Fjx Разложение нагрузки на составляющие в общей системе координат B Fm M B Fmx x Замена заданных нагрузок расчётными узловыми нагрузками ( сосредоточенными силами в расчётных точках загружения ) 1. Границы дисков (узлы) Расчетные 2. Места сечений с искомыми необходимые; точки для СОС – и достаточные внутренними усилиями загружения: 3. Любые точки – дополнительные ( нужны для обеспечения требуемой Способ приведения j заданных нагрузок к расчётным точкам – статически эквивалентное преобразование в пределах расчётного участка Fj, j ( в случае линейной Л.В. результат – точный ) j точности при нелинейных Л.В. в СНС ) j+1 aj Rj bj Fj, j + 1 j j+1 Равнодействующая: Rj = S yF(j); aj = S bj mj,F(j)/Rj Fj, j Rj a j bj эквивалентные aj Fj, j 1 Rj a j bj расчётные узловые нагрузки Матрицы влияния Общий случай загружения ( сосредоточенные и распределённые, силовые и моментные нагрузки ) S = L S* F Fx LS = [ LSx LSy LSz ] F Fy Fz От Fx= 1 От Fy= 1 От Fz= 1 y В общем случае пространственной системы F1y F2y Fjy qy A qx F2x M Fjx Разложение нагрузки на составляющие в общей системе координат B Fmx x Замена заданных нагрузок расчётными узловыми нагрузками ( сосредоточенными силами в расчётных точках загружения ) 1. Границы дисков (узлы) Расчётные 2. Места сечений с искомыми необходимые; точки для СОС – и достаточные внутренними усилиями загружения: 3. Любые точки – дополнительные ( нужны для обеспечения требуемой Способ приведения j заданных нагрузок к расчётным точкам – статически эквивалентное преобразование в пределах расчётного участка Fj, j ( в случае линейной Л.В. результат – точный ) j точности при нелинейных Л.В. в СНС ) j+1 aj Rj bj Fj, j + 1 j j+1 Равнодействующая: Rj = S yF(j); aj = S bj mj,F(j)/Rj Fj, j Rj a j bj эквивалентные aj Fj, j 1 Rj a j bj расчётные узловые нагрузки Матрицы П р и м е р q = 10 кН/м М = 20 кН*м F = 60 кН q = 10 кН/м влияния А 2м 2 2 2 3 1 3 2 4 2 2 VA S M1 ? Q 2 Расчётные точки загружения и участки: 1 2 1 2 3 3 4 5 4 6 5 7 6 8 Замена заданных нагрузок расчётными узловыми нагрузками 50 q q Rq= 40 86 Вектор M q 4 R4= 20 R2= 20 расчетных 0 узловых 5 30 5 F F нагрузок: y 4 40 16 10 10 20 20 10 25 F2,1= 70 F5,4= 10 F6,4= 10 F7,5= 25 25 F3,3= 0 F2,2= 16 F7,6= 0 F6,5= 15 F3,2= 4 F4,3= 0 F8,6= 0 0 Rq= 60 F = 60 q 30 20 F1,1= 50 F1= 50 F2= 86 F6= 25 F = 10 5 F3 = 4 F4 = 0 F7= 25 F8 = 0 1 2 3 4 5 6 7 8 Расчётные точки загружения Матрицы П р и м е р q = 10 кН/м М = 20 кН*м F = 60 кН q = 10 кН/м влияния А 2м 2 2 2 1 3 3 2 4 2 2 VA S M1 ? Q 2 Расчётные точки загружения и участки: 1 2 1 3 2 3 4 5 4 6 5 7 6 8 Формирование матрицы влияния искомых силовых факторов 1,333 1 0,5 0 1,5 0,667 0 0,333 1 1 0,167 Расчётные точки загружения: 0 1 0,5 λV 0,667 1,333 0,5 0 A ΛS ΛSy λ M 1 0,5 1 1,5 0 λQ 2 0,167 0,333 0,5 1 1 2 3 4 0 0 Л.В. 0 0 Л.В. M1 0 0 Л.В. Q2 0,333 0,5 0,333 0 0,333 0 0 1 0 0 0,333 0 5 6 7 0 0 0 8 50 86 4 0 F 10 25 25 VA 0 VA 75 S M1 ΛS F 80 Q 10 2 РАСЧЁТНЫЕ УСИЛИЯ И ОБЪЕМЛЮЩИЕ ЭПЮРЫ Расчётным значением силового фактора S ( расчётным усилием ) называется его экстремальное ( максимальное Smax или минимальное Smin ) значение от совместного действия постоянной нагрузки и временных воздействий, каждое из которых занимает невыгоднейшее ( опасное) – соответственно по максимуму или минимуму фактора S – положение на сооружении. x xr F1 F F2 F3 xl p q Постоянная (const) нагрузка Временные (temp) нагрузки Stemp= S Stemp, i Sconst Stemp ( = Stemp(x, xl , xr ) ) График изменения расчётных усилий Smax Sconst Stemp, max Smax и Smin по длине элементов Sрасч ( или их объему – для нестержневых S S S const temp, min элементов ) называется min Объемлющая эпюра S ( эпюра S ) объемлющей эпюрой силового фактора S. расч имеет две ветви – Smax и Smin ; которые являются границами области возможных значений силового фактора S ( значений S при произвольных положениях временных нагрузок ): Smin S Smax Smax Smin РАСЧЁТНЫЕ УСИЛИЯ И ОБЪЕМЛЮЩИЕ ЭПЮРЫ Расчётным значением силового фактора S ( расчётным усилием ) называется его экстремальное ( максимальное Smax или минимальное Smin ) значение от совместного действия постоянной нагрузки и временных воздействий, каждое из которых занимает невыгоднейшее ( опасное) – соответственно по максимуму или минимуму фактора S – положение на сооружении. Алгоритм определения расчётных усилий и построения объемлющей эпюры 1. Назначаются сечения 1, 2, …, j, …, m в которых будут определяться расчётные усилия ( расчётные сечения ). 2. В назначенных сечениях определяются усилия от постоянной нагрузки Sj,const ( j = 1, 2, …, m ) – строится эпюра Sconst . 3. Строятся линии влияния усилий в назначенных сечениях – Л.В. Sj ( j = 1, 2, …, m ). П р и м е р - иллюстрация Построение объемлющей эпюры М q p F …j… 1 2 3… …m const temp Эпюра Mconst Mj, const M2, const 4. Каждая Л.В. Sj ( j = 1, 2, …, m ) загружается временными нагрузками на max и min усилия. Определяются Sj, temp, max и Sj, temp, min . 5. Для каждого сечения ( j = 1, 2, …, m ) вычисляется пара расчётных значений Sj, max и S j, min . 6. По найденным парам расчётных усилий во всех сечениях строится объемлющая эпюра S . p p F1 F2 F1 F2 Mj, temp, min Л.В. Mj Mj, temp, max p F1 F2 Mmin Эпюра Mрасч Mmax Mj, max Mj, min РАСЧЁТНЫЕ УСИЛИЯ И ОБЪЕМЛЮЩИЕ ЭПЮРЫ З а м е ч а н и е: для выполнения практических расчётов конструкций на прочность при сложном сопротивлении, кроме расчётных усилий (в первую очередь, изгибающих моментов), необходимы также возникающие одновременно с ними ( при той же комбинации воздействий ) другие силовые факторы – поперечные и продольные силы, а в пространственных системах также крутящие моменты: Мрасч Алгоритм определения расчётных усилий и построения объемлющей эпюры 1. Назначаются сечения 1, 2, …, j, …, m в которых будут определяться расчётные усилия ( расчётные сечения ). 2. В назначенных сечениях определяются усилия от постоянной нагрузки Sj,const ( j = 1, 2, …, m ) – строится эпюра Sconst . 3. Строятся линии влияния усилий в назначенных сечениях – Л.В. Sj ( j = 1, 2, …, m ). Qсоотв , Nсоотв П р и м е р - иллюстрация Построение объемлющей эпюры М q p F …j… 1 2 3… …m const temp Эпюра Mconst Mj, const M2, const 4. Каждая Л.В. Sj ( j = 1, 2, …, m ) загружается временными нагрузками на max и min усилия. Определяются Sj, temp, max и Sj, temp, min . 5. Для каждого сечения ( j = 1, 2, …, m ) вычисляется пара расчётных значений Sj, max и S j, min . 6. По найденным парам расчётных усилий во всех сечениях строится объемлющая эпюра S . p p F1 F2 F1 F2 Mj, temp, min Л.В. Mj Mj, temp, max p F1 F2 Mmin Эпюра Mрасч Mmax Mj, max Mj, min Контрольные вопросы ( в скобках даны номера слайдов, на которых можно найти ответы на вопросы; для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*); для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши и выбрать «Перейти к слайду 32» ) 1. Какая операция называется загружением линии влияния? ( 2 ) 2. По каким формулам с помощью линии влияния вычисляется силовой фактор S а) от сосредоточенной нагрузки F? ( 3 ) б) от сосредоточенного момента М? ( 4 ) в) от распределённой нагрузки q(x)? ( 5 ) г) от равномерно распределённой нагрузки? ( 5 ) 3. Правила знаков, используемые в операции загружения линии влияния – ? ( 6 ) 4. Что такое статически эквивалентное преобразование нагрузок ( 7 ) и как его можно использовать при загружении линий влияния? ( 8 ) 5. Условие экстремума силового фактора S при действии подвижной нагрузки – ? ( 9 ) 6. Как записываются условия максимума и минимума S в случае кусочно-линейной линии влияния? ( 10 ) 7. Как определяются опасные положения подвижных нагрузок и соответствующие им экстремальные значения фактора S в случаях: а) одиночной сосредоточенной подвижной силы F? ( 11 ) б) подвижной полосы равномерно распределённой нагрузки q? ( 12 ) 8. Как располагается равномерно распределённая нагрузка q с произвольным разрывами при загружениях на максимум и минимум силового фактора S? ( 13 ) 9. Критерий опасного положения подвижной системы параллельных сосредоточенных сил в случае полигональной линии влияния – ? ( 16 ) 10. Что такое критический груз? ( 17 ) 11. Критерий опасного положения подвижной системы параллельных сосредоточенных сил в случае треугольной линии влияния: а) аналитическое выражение критерия – ? ( 18–21 ) б) графическая интерпретация критерия – ? ( 21, 22 ) 12. Каковы ограничения в использовании критерия определения критического груза при треугольной линии влияния? ( 23 ) ____________________________________________________________ *) Только в режиме «Показ слайдов» Контрольные вопросы ( в скобках даны номера слайдов, на которых можно найти ответы на вопросы; для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*); для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши и выбрать «Перейти к слайду 33» ) 13. По какой матричной формуле вычисляется совокупность ( вектор ) искомых силовых факторов S? ( 24 ) 14. Что такое матрица влияния силовых факторов? ( 24 ) Как она формируется ( смысл строк матрицы влияния )? ( 24 ) 15. Какие величины включаются в вектор F при нагрузках, отличных от сосредоточенных сил? ( 25 ) 16. По каким правилам назначаются расчётные точки загружения? ( 25 ) 17. Как выполняется приведение заданных произвольных нагрузок к расчётным точкам загружения? ( 25 ) 18. Если нагрузки на рассчитываемую систему изменяются, то нужно ли вносить изменения в матрицу влияния силовых факторов? ( 25 ) 19. Какова структура матрицы влияния силовых факторов и вектора расчётных узловых нагрузок в случаях двух- и трёхмерных систем? ( 26 ) 19. Что называется расчётными усилиями и как они вычисляются? ( 29 ) 20. Какие усилия называются соответствующими расчётным усилиям? ( 31 ) 21. Что такое объемлющая эпюра некоторого силового фактора? ( 29 ) 21. По какому алгоритму осуществляется построение объемлющей эпюры? ( 30 ) 22. Как по объемлющей эпюре определить область возможных значений силового фактора S? ( 29 ) ___________________________________ *) Только в режиме «Показ слайдов»