ВСЕРОССИЙСКИЙ ИНТЕРНЕТ-КОНКУРС ПЕДАГОГИЧЕСКОГО ТВОРЧЕСТВА (2013/14 учебный год)
реклама

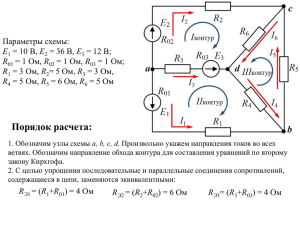
ВСЕРОССИЙСКИЙ ИНТЕРНЕТ-КОНКУРС ПЕДАГОГИЧЕСКОГО ТВОРЧЕСТВА (2013/14 учебный год) Государственное бюджетное образовательное учреждение среднего профессионального образования (ССУЗ) «Златоустовский индустриальный колледж им. П. П. Аносова» Номинация конкурса: Педагогические идеи и технологии: профессиональное образование Конспект урока по теме «Методы расчёта цепей постоянного тока» Дисциплина: «Электротехника и электроника» Специальность: 140448 «Техническая эксплуатация и обслуживание электрического и электромеханического оборудования» Автор: Войсковая Елена Юрьевна, преподаватель специальных дисциплин ГБОУ СПО (ССУЗ) «ЗлатИК им. П. П. Аносова», высшая категория Место выполнения работы: ГБОУ СПО (ССУЗ) «ЗлатИК им. П. П. Аносова», г. Златоуст Челябинской области, ул. Таганайская 2 МЕТОДЫ РАСЧЕТА СЛОЖНЫХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА это электрическая цепь, которая не сводится к последовательному и Сложная параллельному соединению потребителей. электрическая цепь Электрический узел Электрическая ветвь Контур это точка цепи, в которой соединяются три и более ветви. это единственный путь тока от узла к узлу. это любой замкнутый путь, по которому проходит электрический ток. Независимый контур Контур, который имеет только одну общую ветвь с другими контурами Зависимый контур Контур, который получается путем сложение нескольких независимых IV 1 VII R1 E2 I2 B R7 А12С; АВ; ВС; С3D; ВD; D4А D 4 Если ветвь содержит источник ЭДС, то направление тока совпадает с R3 направлением ЭДС. Если ветвь не содержит источника ЭДС, то E3 направление тока задается произвольно III R4 I5 C В каждой ветви задается направление тока I6 I4 II I3 V Схема содержит 4 узла: А; В; С; D 6 ветвей: R6 E4 R5 2 E1 I R2 A I1 3 Контуры обозначаются римскими цифрами. Обход конура задается по часовой стрелке Независимые контуры I - А12СВА; II - ABD4A; III - ВС3DB; Зависимые контуры IV - 12C3D4A1; V - ABC3D4A VI – А12С3DBA; VII – A12CBD4A Законы Кирхгофа Первый закон Кирхгофа. Применяется для узла электрической цепи В ветвях, образующих узел электрической цепи, алгебраическая сумма токов равна нулю. I 0 « + » если ток в ветви направлен к узлу « - » если ток в ветви направлен от узла n I1 I5 I3 I1 I2 I4 I 5 I 2 I1 I 4 I 3 0 I4 I5 I3 I6 I2 I 2 I 5 I1 I 4 I 3 I 6 0 Сумма токов входящих в узел равна сумме токов выходящих из узла I 5 I1 I 3 I 4 I 2 I 2 I1 I 3 I 4 I 5 I 6 Второй закон Кирхгофа. Применяется для контура электрической цепи. Алгебраическая сумма ЭДС источников в замкнутом контуре равна алгебраической сумме падений напряжения на элементах данного контура. Е I k n Rn « + » Если направление ЭДС и тока совпадает с направлением обхода контура « - » Если направление ЭДС и тока не совпадает с направлением обхода контура R1 1 E1 I 1 II I2 R2 A E2 B R3 I3 R4 III Контур I E2 I 2 R2 I 3 R3 R4 R5 I R5 4 2 3 Контур II E1 E2 I1R1 I 2 R2 Контур III E1 I1R1 I 3 R3 R4 R5 R1 E1 I 1 I A E2 I2 R2 IV II I 5 I 2 I1 0 R3 I4 III R4 E3 R7 D V Первый закон Кирхгофа. Узел А C I6 E4 R5 I5 B R6 Контур I I3 Второй закон Кирхгофа. E1 E2 I1R1 I 6 R6 I 2 R2 I2 I4 I6 0 Контур II E2 E4 I 2 R2 I 4 R4 I 5 ( R5 R7 ) E3 E4 I 6 R6 I 3 R3 I 4 R4 Узел С I 6 I1 I 3 0 Контур III Узел D I3 I 4 I5 0 Узел В Контур IV E1 E3 I1R1 I 3 R3 I 5 ( R5 R7 ) Контур V E2 E3 I 2 R2 I 6 R6 I 3 R3 I 5 ( R5 R7 ) Метод узловых и контурных уравнений Является основным методом. Позволяет рассчитать цепь любой сложности Цель расчета: Определение токов в ветвях Порядок расчёта. 1. Определить количество узлов, ветвей и независимых контуров в цепи. В каждой ветви задать направление тока. 2. Записать уравнения по первому закону Кирхгофа. Количество уравнений на 1 меньше чем узлов. 3. Задать направления обходов в каждом независимом контуре и записать уравнения по второму закону Кирхгофа. 4. Общее количество уравнений в системе должно быть равно количеству неизвестных токов в цепи. R1 E1 I 1 I A I2 E2 R2 II C I6 E4 R5 I5 B R6 R3 I4 III R4 E3 R7 D Количество неизвестных токов - 6 Общее количество уравнений в системе - 6 Количество узлов - 4 Уравнений по I закону - 3 Уравнений по II закону - 3 I3 I 2 I 4 I 6 0 I I I 0 6 1 3 I 3 I 4 I 5 0 E1 E 2 I 1 R1 I 2 R2 I 6 R6 E 2 E 4 I 2 R2 I 4 R4 I 5 R5 R7 E3 E 4 I 3 R3 I 4 R4 I 6 R6 Метод контурных уравнений Цель расчета: Определение токов в ветвях Основан на втором законе Кирхгофа Является универсальным и рациональным методом и позволяет рассчитать цепь любой сложности. Контурный ток – это ток протекающий по элементам одного контура. Порядок расчёта. 1. Задать направление основных токов в ветвях. 2. Определить количество независимых контуров и задать направление контурного тока. 3. Выразить основные токи в ветвях через контурные токи: - если ветвь принадлежит только одному контуру, то ток в ней равен контурному; - если ветвь одновременно принадлежит двум контурам, то ток в ней равен алгебраической сумме контурных токов. « + » если направление основного тока и контурного тока совпадают «-» если направление основного тока и контурного тока не совпадают 4. Для каждого независимого контура составить уравнения по II закону Кирхгофа с учётом контурных токов Контурный ток протекает по всем элементам этого контура. Если ветвь принадлежит двум контурам, то ток второго контура берётся со знаком «-» R1 III I5 B R6 C I6 E4 R5 Схема содержит 4 узла, 6 ветвей, 3 независимых контура II E2 I2 R2 A E1 I 1 R3 I4 IIII R4 R7 D I3 E3 3 контурных тока: II ; III ; IIII Независимые ветви I1 I I I 3 I III I 5 I II Зависимые ветви I 2 I II I I I 4 I II I III I 6 I III I I Система уравнений по II закону Кирхгофа E1 E2 I I R1 R2 R6 I II R2 I III R6 E2 Е4 I II R 4 R2 R5 R7 I I R2 I III R3 E3 Е4 I III R3 R4 R6 I II R4 I I R6 Метод узлового напряжения Цель расчета: Определение узлового напряжения Основан на первом законе Кирхгофа Применяется для схем только с двумя узлами. При расчёте необходимо все токи направить в одном направлении Порядок расчёта. 1. Направить токи во всех ветвях в одном направлении. 2. Для каждой ветви определить величину проводимости. g 1 R 3. Для каждой ветви записать уравнение для узлового напряжения с учётом зависимостей, приведённых в таблице 1 4. Из полученных уравнений выразить величину тока. 5. Составить уравнение по первому закону Кирхгофа и подставить в него полученные значения токов. 6. Определить величину узлового напряжения и токи в ветвях. Формулы для определения узлового напряжения с учетом направления обхода Е I R Обход Е I R Обход Е I R Обход Е I А R А А А Обход В U AB E IR В U AB E IR В U AB E IR В U AB E IR Пример расчёта Необходимо определить токи в ветвях методом узлового напряжения R1 E1 I 1 1. Определить проводимость ветвей 1 1 g1 g 2 E3 E2 R1 R2 I2 R2 B A 1 g3 R3 R4 R5 R5 R3 2. Записать уравнение для узлового Обход I 3 R4 напряжения для каждой из ветви и выразить величину тока U BA E1 I1R1 U BA E1 I1 U BA g1 E1 g1 R1 U BA E2 E3 I 2 R2 U BA E2 E3 I2 U BA g 2 ( E2 E3 ) g 2 R2 U BA I 3 R5 R4 R3 U BA I3 U BA g 3 R3 R4 R5 3. Составить уравнение по первому закону Кирхгофа и подставить в него значение токов I1 I 2 I 3 0 U BA g1 E1 g1 U BA g 2 ( E2 E3 ) g 2 U BA g3 0 U BA ( g1 g 2 g3 ) E1 g1 ( E2 E3 ) g 2 E1 g1 ( E2 E3 ) g 2 U BA g1 g 2 g 3 Определить величину узлового напряжения UAC E1 I 1 R1 A I2 E2 R2 R6 C R5 I3 обход R3 E3 R4 U AC E1 I1R1 U AC E2 I 2 ( R2 R6 ) U AC E3 I 3 R5 R4 R3