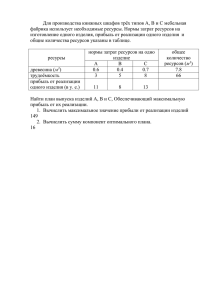
Построение морфологических спектров по параметру сложности

Критериальные
морфологические спектры
Визильтер Ю.В., Сидякин С.В.
viz@gosniias.ru, sersid@bk.ru
Москва,
ФГУП “Государственный научноисследовательский институт авиационных систем”
Морфология Серра
Структурирующий элемент
Трансляция
T
BT
B
Исходный образ
A
Базовые операции ММ
Сжатие AB
Расширение AB
A
AB
A
Морфологические фильтры
Открытие: X○B = (XB)B
Закрытие: X●B = (XB)B
Морфология Серра
Структурирующий элемент
T
Исходный образ
BT
B
Трансляция
Открытие: X○B = (XB)B
Закрытие: X●B = (XB)B
Идея построения морфологического спектра
rB
X
r
XrB
X◦rB








Скачкообразное
изменение площади
фигуры на размер
объекта
Формальное определение морфологического спектра
PSX(r,B) = - S(X◦rB)/r, r0,
(1)
PSX(-r,B) = S(X●rB)/r, r>0,
(2)
где S(X◦B) – площадь открытия образа Х элементом B
Морфологический спектр с круглым структурирующим элементом
и этапы морфологической обработки изображения при его построении.
Критериальная проективная морфология
Критерий морфологического риска
F ( A, L)  J ( A, L)    Q(L)
A, L- одномерные (сигналы) или двумерные (изображения) функции,
обобщенно называемые также образами
J(A,L)– функционал (критерий) соответствия L и A;
Q(L)– функционал (критерий) качества морфологической реконструкции L;
α - параметр морфологической сложности оператора ψα
Оператор максимально достоверной морфологической реконструкции
  A  argmin L F  A, L
Критериальный морфологический спектр по параметру
морфологической сложности α:
PS ( A,  )  J ( A, r ( ) A) /    J r ( A, r ( ) A)r ( )
J r ( A, r ( ) A)  J ( A, r ( ) A) / r r ( )  r( ) / 
Алгоритм дискретного приближения морфологического спектра сложности
Fα(A,r) = (1- α)S(A◦rB) + αS(ArB), α[0,1]
1
ЭТАП
Задать шаг (дискрет) r и диапазон [rmin, rmax] вычислений по r.
Задать шаг (дискрет) α вычислений по α.
С выбранным шагом r для всех точек диапазона r[rmin, rmax]:
Вычислить площади открытия S(r)=S(A◦rB), сжатия S(ArB).
С выбранным шагом α для всех точек диапазона α[0,1] вычислить
значения функции-критерия Fα(A,r).
4. С выбранным шагом α для всех точек диапазона α[0,1] вычислить
значения:
1.
2.
3.
•
•
r(A,α) = arg minr[rmin, rmax] Fα(A,r)
5. С выбранным шагом r для всех точек диапазона r[rmin, rmax] вычислить
дискретный морфологический спектр по параметру r:
PS(r) = S(r) - S(r+r)
2
ЭТАП
6. С выбранным шагом α для всех точек диапазона α[0,1] вычислить
дискретную производную r (α):
r ( )  r (   ) - r ( -  )
7. Подставляя зависимость r(α) в зависимость PS(r), рассчитать значения
морфологического спектра по параметру сложности:
PS ( A, )  PS (r( ))r ( )
A
анализируемый объект
Первый этап (характерные зависимости)
Fα(r)
2r
структурирующий
элемент (квадрат)
шаг r =2
шаг α= 0,05
Второй этап (характерные зависимости)
S(r)  S ( A B(r)) / S ( A)
r( )  arg min Fα (r)
r
r
PS (r)   S (r)
r
r=21
r=26
Нормализованный спектр по параметру r
r=24
r=31
Пиковые составляющие формы фигуры А
PS ( )  PS (r)r ( )
Нормализованный спектр по
параметру α (PS(α)), для
пересчета использовались
зависимости PS(r) и r(α).
Нормализованный спектр по параметру α
Построение непрерывных критериальных
морфологических спектров
Рассмотрим критерий морфологического риска:
Fa(A,L) = J(A,L) + αQ(L)
Функция, представляющая собой минимум критерия морфологического риска
от параметра морфологической сложности:
F(α)=minαFa(A,L) - кусочно–линейная функция с конечным числом линейных участков
Решения L1,…,Lk L, оптимальные, по крайней мере,
для одного значения параметра α - доминантные решения.
Геометрическая интерпретация построения кусочно-линейной функции минимума
критерия морфологического риска от параметра морфологической сложности α
Дано I=[αmin,αmax], необходимо вычислить
L1,…,Lk и I1=[αmin,α1], I1=[α1,α2],…,Ik=[αk-1,αmax],
где решение Li оптимально на αIi и
sup Ii ≤ inf Ij для Ii,Ij (j=i+1).
Алгоритм вычисления всех узловых точек нижней огибающей αi  [αmin,αmax]:
Шаг 1. Вычислить значения Lmin,Lmax для αmin,αmax
если Lmin=Lmax, то инициализировать список (Lmin, [αmin,αmax]),
иначе инициализировать список (Lmin,{ αmin}),( Lmax,{ αmax }).
Шаг 2. Пока между соседними элементами рассматриваемого списка существует пустой
интервал, то есть (αi,αj)=(sup Ii, inf Ij)≠ :
Решить линейное уравнение Fα(A,Li)=Fα(A,Lj), найти α,
если αi является решением, то установить границы j-го интервала следующим образом
Ij= Ij U [αi,αj].
если αj является решением, то установить границы i-го интервала следующим образом
Ii= Ii U [αi,αj].
иначе α - единственное решение на интервале α  (αi,αj):
вычислить L для Fα(A,L).
если L =Li или L= Lj, то установить значения интервалов Ii, Ij следующим образом:
Ii= Ii U [αi,α], Ij= Ij U [α,αj],
иначе добавить элемент в список следующим образом:
(L,{α}) между (Li,Ii ) и (Lj,Ij).
После вычисления решения L для α  (αi,αj) нужно решить какой интервал обрабатывать
следующим.
Для этого последовательно просматриваются все интервалы на отрезке [αmin,αmax] и
выбирается тот, для которого (sup Ii, inf Ij) ≠  .
Шаг 3. Если ни один интервал на отрезке [αmin,αmax] не удовлетворяет условию
(sup Ii, inf Ij) ≠ , то завершить работу.
Схема вычисления непрерывных критериальных морфологических спектров
Fα(A,r) = (1- α)S(A◦rB) + αS(ArB), α[0,1]
A
Дискретный
спектр
Анализируем объект
с точки зрения
занимаемой им
F min(  )  min r F (r)
площади
Непрерывный
спектр
Площадь открытия S от параметра α
Этапы построения морфологического спектра контура фигуры
по параметру сложности α
F(A,L) = –J(L) + Q(L)  min(L), α≥0
где J(L) – длина контура бинарной фигуры,
Q(L) – число узловых точек ломаной (многоугольного контура).
Fmin()

а - график минимума функции - критерия морфологического риска от параметра
морфологической сложности α;
b - чередующиеся зеленые и красные линии соответствуют областям, на которых
значение функции решения остается постоянным (длина контура не меняется)
L
=5
=24

Зависимость длины контура фигуры от
параметра морфологической сложности α
L/
=26

Спектр контура фигуры от параметра
морфологической сложности α
=45
=38
=47
Заключение
Предложен новый подход к вычислению дискретных и
непрерывных критериальных морфологических спектров по
параметру морфологической сложности, основанный на
критериальных проективных морфологиях. Основная идея
рассматриваемого алгоритма заключается в построении
кусочно-линейной
функции
минимума
критерия
морфологического риска от параметра морфологической
сложности α. После этого полученный результат позволяет
формировать точное, а не приближенное, представление
морфологических
информативность,
спектров,
а
что
следовательно,
повышает
и
их
потенциальное
качество сравнения таких спектров между собой.
Спасибо за внимание!