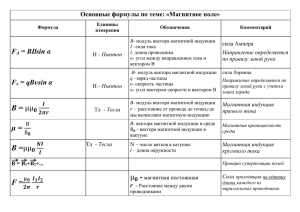
rotB j
реклама

3.20 Напряженность магнитного поля Применим операцию ротор к уравнению (3.19.1) ' 0 Ранее было получено rotB rotB rotB rotB0 0 j где j - плотность макроскопического тока. Аналогичная формула имеет место и для вектора ' собственной магнитной индукции B rotB 0 jмол ' где jмол - плотность молекулярных токов. Поэтому ротор результирующего магнитного поля в веществе можно записать в виде rotB [ B] 0 ( j jмол ) j (3.20.1) Плотность молекулярных токов мол сама зависит от магнитной индукции В. Поэтому, чтобы найти rotB надо знать плотность не только макроскопических, но и молекулярных токов, что сопряжено с определенными трудностями. Чтобы обойти эти трудности, найдем величину, которая определяется только макроскопическими токами. Для этого выразим плотность молекулярных токов через намагниченность . J Рассмотрим некоторый замкнутый контур Г внутри вещества. Сумма всех молекулярных токов, протекающих через такой контур, равна j мол dS S где S – поверхность, натянутая на контур Г. В данный интеграл вклад дают лишь те молекулярные токи Iмол, которые нанизаны на контур и пересекают поверхность S только один раз. Пусть dl – элемент контура, образующий с намагниченностью J угол . На этот элемент нанизаны молекулярные токи, центры которых находятся внутри косого цилиндра. Объем цилиндра равен S мол cos dl где S мол - площадь, охватываемая одним молекулярным током (основание цилиндра). Пусть n - концентрация молекул, тогда ток, охватываемый элементом контура dl, равен nI мол S мол cos dl Но этой формуле можно дать и другую интерпретацию. Действительно, произведение I S - есть магнитный момент pm мол мол одного молекулярного тока. Поэтому nI мол S мол - есть магнитный момент единицы объема, и значит, согласно определению (3.19.2), равен модулю вектора намагниченности J . Тогда величину nI мол S мол cos можно рассматривать как проекцию вектора намагниченности на направление элемента контура dl. Поэтому молекулярный ток, охватываемый элементом dl, можно записать как (Jdl) . J В результате ток, созданный молекулами, находящимися вблизи элемента контура dl равен nI мол S мол cos dl ( Jd l ) Итак, сумма всех охватываемых контуром Г молекулярных есть j мол dS токов, Jdl Г S Преобразуем правый интеграл с помощью теоремы Стокса Jdl [ J ] dS Г S В результате получаем равенство S jмол dS [ J ]dS S которое должно выполняться при произвольном выборе контура Г и поверхности S. А это возможно, лишь если равны подинтегральные функции jмол [ J ] (3.20.2) Следовательно, плотность молекулярных токов равна ротору вектора намагниченности. Подставим (3.20.2) в (3.20.1) [ B] 0 j 0[ J ] Это уравнение можно переписать в виде [ ( B 0 J )] j Откуда следует, что вектор (3.20.3) B H= -J μ0 (3.20.4) определяется только плотностью макротоков . j Вектор H называется напряженностью магнитного поля. Он характеризует магнитное поле макротоков. С учетом (3.20.4) формула (3.20.3) принимает вид [ H] = j (3.20.5) Ротор напряженности магнитного поля равен вектору плотности макроскопических токов. Возьмем поверхностный интеграл от обеих частей этого равенства по поверхности S, натянутой на замкнутый контур Г [ H]dS = jdS S S Согласно теореме Стокса левый интеграл можно представить в виде [ H]dS = S Hdl Г Следовательно H dl jdS I Г S (3.20.6) Если макроскопические токи текут по нескольким проводам, охватываемым контуром, то формула (3.20.6) принимает вид Hdl I k k Г Формулы (3.20.7) (3.20.7) выражают собой теорему о циркуляции вектора напряженности H : циркуляция вектора напряженности магнитного поля по некоторому контуру равна алгебраической сумме макроскопических токов, охватываемых этим контуром. Напряженность магнитного поля H является аналогом электрического смещения D . (3.20.6) и Из (3.20.7) магнитного поля следует размерность напряженности A [H ] м Согласно (3.20.4) такую же размерность имеет и намагниченность J . Опыт показывает, что в не сильных магнитных полях намагниченность пропорциональна напряженности магнитного поля J H где - магнитная безразмерная величина. восприимчивость (3.20.8) магнетика, Подставим (3.20.8) в (3.20.4) Откуда Величина B H= - H μ0 B H= μ0 (1 + ) (3.20.9) 1 (3.20.10) называется магнитной проницаемостью вещества. Магнитная проницаемость показывает во сколько раз магнитное поле макротоков изменяется в магнетике за счет поля микротоков. Формулу (3.20.9) можно переписать в виде B H= μ0 (3.20.11) В изотропных средах направления векторов индукции В и напряженности Н совпадают. В анизотропных средах направления векторов В и Н могут не совпадать. Рассмотрим магнитное поле в вакууме. У вакуума магнитная восприимчивость и намагниченность равны нулю, а магнитная проницаемость равна единице 0 J =0 1 Поэтому напряженность магнитного поля в вакууме связана с магнитной индукцией формулой B H= μ0 Найдем для примера напряженность магнитного поля прямого тока, текущего в магнетике. Согласно (3.3.1) магнитная индукция прямого тока равна 0 I B 2 R Подставляя в (3.20.11), получаем напряженность магнитного поля прямого тока в магнетике I H= 2π R (3.20.12) 3.21 Условия на границе раздела двух магнетиков Пусть имеются два однородных магнитными проницаемостями 1 и магнетика 2 . Найдем связь векторов В и Н в двух средах на границе их раздела. Построим вблизи границы цилиндр с высотой h и n основаниями S . Внешние нормали n и n' к основаниям направлены в противоположные стороны. с S μ2 h μ1 n' Согласно теореме Гаусса поток магнитной индукции ФВ через замкнутую поверхность цилиндра равен нулю ФВ BdS 0 (3.21.1) S С другой стороны, этот поток можно представить как сумму потоков через два основания и боковую поверхность цилиндра ФВ B1n 'S B2n S Bnбок Sбок 0 Устремим высоту цилиндра к нулю h 0, тогда потоком через боковую поверхность можно пренебречь и получаем B1n ' B2 n 0 Спроецируем вектора индукции ту же нормаль (например получим n В1 и В2 на одну и ), тогда знак изменится и B1n = B2n Нормальная составляющая вектора индукции на границе магнетиков непрерывна. (3.21.2) магнитной Используя (3.20.11), переписать в виде равенство H 1n 2 = H 2n 1 или (3.21.2) можем (3.21.3) 1 H 1n = 2 H 2n Следовательно, нормальная составляющая вектора напряженности магнитного поля на границе магнетиков терпит разрыв. Теперь выберем вблизи границы прямоугольный контур АВCD длиной l = АВ и высотой h = AD, и вычислим циркуляцию напряженности контуру. Согласно (3.20.6) ABCD Пусть макроскопические токи по границе не текут, тогда I=0 ABCD и Hdl 0 Н по этому Hdl jdS I S l μ2 μ1 С другой стороны, криволинейный интеграл можно расписать в виде вкладов от его отдельных участков ABCD Hdl H l dl = H 1τ l - H 2τ l + < H l > 2h ABCD где H l - проекция вектора H на направление вектора перемещения d l вдоль контура АВCD. Устремляя h 0, получаем условие непосредственно на границе H 1τ = H 2τ (3.21.4) Тангенциальная составляющая вектора напряженности магнитного поля на границе магнетиков непрерывна. Выражая Откуда Н через В, находим B1τ 0 1 B1τ 1 = B2τ 2 = B2τ 0 2 (3.21.5) Тангенциальная составляющая вектора магнитной индукции Вτ терпит скачок. Итак, на границе раздела магнетиков : 1) нормальная составляющая вектора магнитной индукции Вn и тангенциальная составляющая вектора напряженности магнитного поля Н непрерывны, 2) тангенциальная составляющая вектора магнитной индукции В и нормальная составляющая вектора напряженности Нn терпят скачок. Рассмотрим поведение линий магнитной индукции при пересечении границы. Из рисунка следует, что tg1 B1 / B1n tg 2 B2 / B2 n С учетом (3.21.2) и (3.21.5) получаем tg1 1 tg 2 2 (3.21.6) закон преломления магнитной индукции Из закона преломления следует, что при переходе в магнетик с большей магнитной проницаемостью линии индукции отклоняются от нормали, что приводит к их сгущению. Это используют для магнитной защиты приборов. Приборы окружают железным экраном, в толщине которого происходит сгущение линий магнитной индукции, что приводит к ослаблению магнитного поля внутри экрана. 3.22 Виды магнетиков Формула (3.20.8) J H определяет магнитную восприимчивость единицы объема вещества. Часто используют восприимчивость, отнесенную к одному молю вещества m . Они связаны между собой формулой m Vm где Vm – молярный объем. Поэтому, в то время как m - имеет размерность 3 м [m ] моль величина безразмерная, Vm - В зависимости от знака и величины магнитной восприимчивости все магнетики делят на 3 группы: 1) диамагнетики – χm отрицательна и мала по величине м моль 3 χ m ~ -10 2) парамагнетики – величине 3) ферромагнетики – χm -11 ÷ 10 -10 положительна и тоже мала по м ÷ 10 моль 3 χ m ~ 10 -10 -9 χm положительна и велика по величине м χm ~ 1 моль 3 Следовательно, у парамагнетиков ферромагнетиков намагниченность J совпадает и по направлению с напряженностью магнитного поля Н, Н тогда как у диамагнетиков вектора J направлены в противоположные стороны. и Кроме того, у диамагнетиков и парамагнетиков магнитная восприимчивость χ не зависит от напряженности магнитного поля. В отличие от них у ферромагнетиков магнитная χ восприимчивость является функцией от напряженности магнитного поля. Рассмотрим природу свойств магнетиков подробнее.