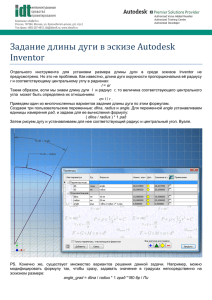
i, j
реклама

Введение в теорию сетевого планирования
Проект
Проект – это список частично упорядоченных работ,
направленных на достижение одной цели.
Работа i предшествует работе j, если работа j не может быть
начата раньше завершения работы i.
Проект считается выполненным, если выполнены все работы
списка.
В любом проекте можно выделить подмножество критических
работ, увеличение продолжительности выполнения которых
приведет к увеличению времени выполнения всего проекта.
При анализе проекта необходимо определить, в частности, min
время его выполнения, а также найти узкие места.
Сеть
Для анализа проекта в теории сетевого планирования исп-ся сеть,
отражающая отношения предшествования работ.
Сеть S=(X, U) – это простой ориентированный ациклический
граф с одним источником и одним стоком
(a, b) - путь из вершины a в вершину b
Вершина i предшествует вершине k, если в сети S путь (i, k).
Дуга (i, k) предшествует дуге (p, q), если в сети S путь (k, p).
Работа i непосредственно предшествует работе j, если i
предшествует j и нет такой работы k, что i предшествует k и k
предшествует j.
Сетевая модель
Сеть наз. взвешенной, если её вершинам или/и дугам приписаны
числа – «веса».
Длиной пути (i, k), обозначим ее |(i, k)|, из вер. i в вер. k в
взвешенной сети явл. весов, включенных в путь элементов.
Обозн. *(i, k) самый длинный путь из вер. i в вер. k.
Сетевая модель (сетевой график) – это представление списка
работ проекта в виде взвешенной сети, которое позволяет
адекватно отразить связи между работами проекта.
2 типа сетевых моделей:
1. «работы-вершины»
2. «работы-дуги»
Типы сетевых моделей
1. «работы-вершины»: вершина – образ работы;
дуги служат для пред. отношения предшествования работ.
Для построения: работе проекта вершина, имеющая вес =
длительности;
дуга (i, j) , если работа i непосредственно предшествует работе j.
2. В моделях «работы-дуги»: работы – дуги;
направление дуги отображает част. порядок на мн. работ.
Вершины соответствуют событиям – моменты завершения одних
работ и возможность начала выполнения других.
Для построения: работе дуга, имеющая вес = длительности.
Из конечной вер. дуги p проводится дуга в начальную вер. дуги q,
если работа p непосредственно предшествует работе q. Дуга,
которая не имеет прообраза в мн. работ и введена для задания
отношения предшествования, наз. фиктивной.
Не фиктивные дуги наз. фактическими.
Упрощение сети
U – мн. фактических дуг сети
Ui – подмн. фактических дуг (1, i)
Ui – подмн. фактических дуг (i, n)
2 сети с одинаковым мн. фактических дуг наз. эквивалентными,
если они представляют одно и то же отношение предшествования
фактических дуг.
Рассмотрим пару вершин i и k:
(1) не инцидентной им обеим фактической дуги
(2) не дуг p, q U :
p
i
– i(p)=i(q), k(p)=i, k(q)=k;
q
k
– или k(p)=k(q), i(p)=i, i(q)=k.
i
i
k
k
p
q
Упрощение сети
Результатом склейки вер. i и k в сети S, удовлетворяющих
свойствам (1) и (2), является сеть S, в кот. вер. k удалена, а все
дуги, кот. были ей инцидентные в S, в S инцидентны вер. i.
Если в S окажется несколько параллельных фиктивных дуг, то
все они, кроме одной, удаляются.
Теорема. Пусть вершины i и k удовлетворяют условиям (1) и (2).
Сеть S, полученная из S в результате склеивания вершин i, k и
исключения k, эквивалентна S Ui = Uk, или Ui = Uk.
Пример упрощения сети
4
8
1
10
3
6
5
2
9
7
Пример упрощения сети
4
8
1
3
10
6
9
2
7
Обозначения
{1, …, n} – вершины;
{1, …, m} – дуги;
1 – источник;
n – сток.
Если первоначально в
сетевой модели имеется
несколько источников (стоков)…
Сетевая модель – разреженная сеть…:
j – номер дуги;
i(j) – номер начальной вер. дуги j;
k(j) – номер конечной вер. дуги j;
j – длина дуги j (продолжительность выполнения
соответствующей работы).
(j)
i(j)
j
k(j)
Параметры сетевой модели
Ранним временем наступления события i наз. величина
Ti E | * (1, i ) |
E
Время T Tn критическое время проекта – min возможное
время выполнения всего проекта
Любой путь *(1, n), а также дуги (работы) и вершины
(события), этому пути, также наз. критическими.
Поздним временем наступления события i наз. величина
Ti L T | * (i, n) |
Если событие i наступит не позднее момента Ti L , то время
выполнения всего проекта не увеличится
Событие i является критическим Ti E Ti L
Резервы выполнения работ
Свободным резервом выполнения работы j наз. величина
TkE( j ) Ti (Ej ) j , кот. = max увеличению продолжительности
выполнения работы j, не меняющему ранние времена наступления
всех событий
Полным резервом выполнения работы j наз. величина
TkL( j ) Ti (Ej ) j . На такую величину можно увеличить
продолжительность выполнения работы j, чтобы не изменилось
критическое время проекта
Критические работы имеют нулевой свободный и полный резервы
Ранг события
Ранг Ri события (вершины) i, равен max количеству дуг в {(1, i)}
Алгоритм Форда:
Шаг 0. вершин i=1,…,n полагаем ri = 0.
Пусть в результате k1 шагов найдены величины ri.
Шаг k. Просматриваем последовательно работы-дуги j=1,…,m и
пересчитываем величины rk(j)=max{rk(j), ri(j)+1}.
Если на каком-то шаге k ни одна из величин ri не изменилась, то
они являются рангами событий, и алг. останавливается. Иначе,
полагаем k=k+1 и повторяем шаг k.
T=O(mn)
M=O(n)
Ранг события
Теорема. В результате вып. k шагов алг. Форда вер. i:
1) ri Ri;
2) ri = Ri, если ранг события i не превосходит k.
Доказательство. Докажем 1) индукцией по рангу события. Для
входа r1 = 0. Предположим неравенство справедливо для событий
рангов 1,…,R. Рассмотрим событие l, ранг которого Rl=R+1. Пусть
k(j)=l и j последняя работа, при рассмотрении кот. изменилась
величина rl (т.е. rl=ri(j)+1). по предположению индукции,
rl=ri(j)+1 ri(j)+1 Ri(j)+1 Rl.
Докажем 2) индукцией по номеру шага алгоритма. На шаге 0 для
един. вер. ранга 0 имеем r1=R1=0. Пусть в результате k1 шагов
величины rl = Rl событий l, ранги которых не превосходят k1,
найдены. Рассмотрим событие l ранга k и работу j такую, что
k(j)=l, Ri(j)=k1. По индукционному предположению и утв. 1)
величина ri(j) не меняется на шаге k и равна Ri(j)
rl ri(j)+1=Ri(j)+1=k.
Правильная нумерация вершин
Нумерация вершин наз. правильной, если i(j)< k(j) дуг j=1,…,m
Зная ранги событий…:
• вход 1;
• вершинам ранга 1 номера 2,…,n1;
• вершины, имеющие ранг 2 номера n1+1,…,n2;
и т. д.
• выход n.
4
5
3
5
8
0
1
4
1
7
3
2
5
6
2
6
7
5
6
1
8
4
2
3
Нахождение ранних времен (алгоритм Форда)
Шаг 0. вершин i=1,…,n полагаем Ti E 0
Пусть в результате k1 шагов найдены значения Ti E
Шаг k. Просматриваем последовательно дуги j=1,…,m и
пересчитываем величины TkE( j ) max{TkE( j ) , Ti (Ej ) j }
Если на шаге k ранние времена событий не меняются, то алг.
останавливается. В противном случае увеличиваем k на единицу и
повторяем шаг k
Правильное упорядочивание дуг
Если дуг p и q, p(1, i(q)) выполняется неравенство p<q, то
говорят, что дуги сети правильно упорядочены
Другими словами, если в проекте работа p предшествует работе q,
то номер соответствующей ей дуги должен быть < номера дуги,
соответствующей работе q
Предположим, вершины занумерованы правильно. Для
получения правильно упорядоченного списка дуг в этом случае
достаточно воспользоваться номерами конечных вершин:
Шаг 0. Положим k=2 и nk=0.
Шаг k. Дуги, входящие в вер. k, нумеруются числами
nk+1,…,nk+mk, где mk=|{i : (i, k)U}|.
Если k n, то k=k+1, nk=nk+mk и повторяем шаг k.
Иначе конец.
Правильное упорядочивание дуг
7
5
5
1
1
3
2
6
4
2
8
9
4
3
7
6
12
11 8
10
Нахождение ранних времен за 1 просмотр дуг
Теорема. Если дуги правильно упорядочены, алгоритм Форда
находит ранние времена наступления событий за один просмотр
дуг в порядке их нумерации j=1,…,m.
Доказательство. Пусть дуги правильно упорядочены и величины
Ti, i=1,…,n, являются ранними временами, вычисленными на 1
шаге алг. Форда. Предположим, что на 2 шаге алг. не остановился.
Значит, вер. l, у кот. раннее время, полученное на
1 шаге Tl < раннего времени Tl, полученного на 2 шаге.
Пусть дуга j является 1-ой в списке, когда величина Tl=Tk(j)
изменилась на 2 шаге алг. Тогда для вер. i(j) раннее время также
изменилось на 2 шаге, т.е. Ti( j ) Ti(j ) .
Но дуги, заканчивающиеся в вер. i(j), имеют номера < j.
Ti( j ) Ti ( j ) и изменение Ti(j) на 2 шаге алг. (до просмотра дуги j)
противоречит выбору j.
Нахождение поздних времен (алгоритм Форда)
Шаг 0. вер. i=1,…,n полагаем Ti L T TnE .
Пусть в результате k1 шагов найдены значения Ti L .
Шаг k. Просматриваем последовательно дуги j=1,…,m и
пересчитываем величины Ti (Lj ) min{ Ti (Lj ) , TkL( j ) j }.
Если на шаге k поздние времена событий не меняются, то алг.
останавливается. В прот. сл. полагаем k=k+1 и повторяем шаг k.
Теорема. В случае правильной упорядоченности дуг, поздние
времена находятся с помощью алгоритма Форда за 1 просмотр
дуг в обратном порядке j=m,…,1.