3.13 Работа, совершаемая при перемещении Поместим в
реклама
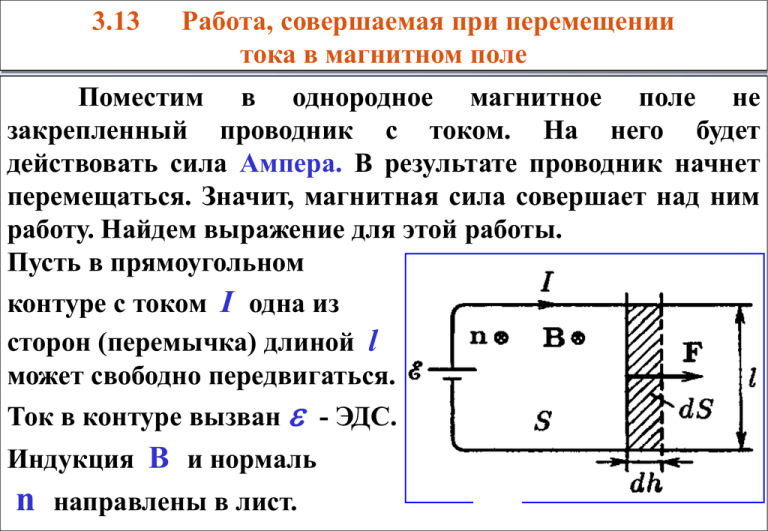
3.13 Работа, совершаемая при перемещении тока в магнитном поле Поместим в однородное магнитное поле не закрепленный проводник с током. На него будет действовать сила Ампера. В результате проводник начнет перемещаться. Значит, магнитная сила совершает над ним работу. Найдем выражение для этой работы. Пусть в прямоугольном контуре с током I одна из сторон (перемычка) длиной l может свободно передвигаться. Ток в контуре вызван - ЭДС. Индукция В и нормаль n направлены в лист. На перемычку действует сила Ампера F = IBl вызывающая ее перемещение на некоторое расстояние На этом пути сила Ампера совершает работу dA = Fdh = IBldh = IBdS = IdФ dh. (3.13.1) Следовательно, работа магнитных сил по перемещению проводника с током равна произведению силы тока на магнитный поток через площадь, пересеченную проводником. Однако, эта работа совершается не за счет энергии внешнего магнитного поля, а за счет источника, поддерживающего постоянным ток в контуре. Теперь найдем работу по перемещению произвольного замкнутого контура (ABCD) с постоянным током I в магнитном поле с индукцией B. Пусть контур лежит в плоскости листа и перемещается под действием силы Ампера на малое расстояние. Вектор магнитной индукции, как и раньше, входит в лист. Разобьем контур (ABCD) на два проводника (АВС) и (СДА), соединенных своими концами. Работа силы Ампера по перемещению контура (ABCD) равна сумме работ по перемещению этих двух проводников dA = dA1 + dA2 где dA1 - работа проводника АВС, проводника СДА. силы dA2 - Ампера по перемещению работа по перемещению Силы Ампера, приложенные к участку АВС, образуют с вектором перемещения тупые углы, поэтому работа этих сил отрицательная dA1 < 0 и ее можно записать как dA1 = -I(dФ0+dФ1), где dФ0 – поток через заштрихованную поверхность, а dФ1 – поток через контур в его начальном положении ABCD. На участке СДА силы Ампера образуют с вектором перемещения острые углы, поэтому их работа положительная dA2 > 0 и ее можно записать как dA2 = I(dФ0+dФ2) где dФ2 – поток через контур в его конечном положении A´B ´ C ´ D ´. Полная работа сил Ампера по перемещению контура равна dA = I(dФ0+dФ2) - I(dФ0+dФ1) = = I(dФ2-dФ1) (3.13.2) где (dФ2 - dФ1) – изменение магнитного потока сквозь площадь контура. Если перемещение конечное, то работа равна интегралу от (3.13.2) A = IФ (3.13.3) Таким образом, работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока Ф, сцепленного с контуром. 3.14 Явление электромагнитной индукции В 1831 году Фарадей обнаружил, что в замкнутом контуре при изменении потока магнитной индукции через поверхность, ограниченную контуром, возникает электрический ток. Этот ток назвали индукционным током. Возникновение индукционного тока указывает на наличие в цепи ЭДС, которую называют ЭДС электромагнитной индукции . Опыт показывает, что i величина не зависит от способа, с помощью которого i осуществляется изменение магнитного потока, а зависит лишь от скорости изменения потока dФ Закон электромагнитной i =индукции Фарадея dt (3.14.1) Знак минус в формуле (3.14.1) определяется правилом Ленца: индукционный ток в контуре всегда направлен так, чтобы противодействовать вызвавшей его причине Это значит, что индукционный ток создает такое магнитное поле, которое препятствует изменению потока, вызвавшему индукционный ток. Рассмотрим явление электромагнитной индукции на примере двух проводников в виде контуров, по одному из которых течет ток. Ток I1 в контуре 1 При увеличении тока ним и поток создает магнитное поле I1 растет и поле Ф, пронизывающий контур 2. Согласно закону Фарадея в контуре 2 возникает индукционный ток I2, который течет против тока I1. Поэтому контуры будут отталкиваться, а поле второго контура В2, будет направлено против поля первого контура В1. I2 В1. В1, а вместе с 2 1 I1 B2 dФ/dt > 0 B1 Если же ток I1 уменьшать, то будет уменьшаться и магнитный поток Ф, пронизывающий контур 2. Поэтому в контуре 2 ЭДС электромагнитной индукции i изменит свой знак, вместе с ней изменит направление и индукционный ток I2 и 2 1 будет течь в том же I2 направлении, что и ток I1. I1 В результате контуры будут притягиваться друг к другу, а созданные ими магнитные поля B 2 будут совпадать по B1 направлению. dФ/dt < 0 Покажем, что закон Фарадея является результатом действия силы Лоренца на электроны в движущихся проводниках. Рассмотрим снова контур с подвижной перемычкой. Поместим его в однородное магнитное поле В, перпендикулярное к плоскости контура и направленное за лист. Туда же направлен и вектор нормали n. Начнем передвигать перемычку со скоростью υ. Вместе с перемычкой будут перемещаться и находящиеся в ней электроны. На каждый электрон действует сила Лоренца, направленная вдоль перемычки FЛ = e[ B] – заряд электрона (е < 0). Действие силы Лоренца эквивалентно действию электрического поля с напряженностью где е E = [ B] Однако, это поле имеет электростатическое происхождение. магнитное, а не Найдем циркуляцию вектора E по замкнутому контуру. Эта циркуляция должна равняться ЭДС в контуре Edl [ B]dl i Направление обхода контура показано на рисунке. Поскольку поле E отлично от нуля лишь на перемычке (участок контура 1-2), то [ B]dl [ B] dl ([ B] l ) 2 2 1 1 i Воспользуемся свойством смешанного произведения ([ B] l ) ([l ] B) i Умножим и разделим правую часть на dt ([l ] B)dt ([l dt ] B) i dt dt Из рисунка следует, что [l dt ] ndS где dS – приращение перемещения контура dt. площади контура за время Поэтому можем записать ( B n )dS ( B dS ) dФ i dt dt dt Таким образом, получили закон Фарадея. Следовательно, роль сторонних сил, вызывающих ЭДС электромагнитной индукции, играет магнитная сила – сила Лоренца. 3.15 Вращение рамки с током Явление электромагнитной индукции используется в генераторах для преобразования механической энергии в электрическую. Рассмотрим принцип действия генератора на примере плоской рамки, вращающейся в однородном магнитном поле В, созданном постоянным магнитом. Магнитный поток, пронизывающий рамку равен Ф ( B S ) BS cos Пусть рамка вращается (за счет энергии пара, воды и т.д.) с постоянной угловой скоростью . Тогда угол между нормалью к поверхности рамки магнитной индукции В n и вектором будет зависеть от времени Магнитный поток гармоническому закону = t меняется Ф BS cos(t ) со временем по При вращении рамки в ней возникает переменная ЭДС электромагнитной индукции , изменяющаяся тоже i по гармоническому закону dФ BS sin(t ) i dt Эта переменная ЭДС снимается с вращающегося витка с помощью щеток (см. рисунок). В России принята частота = /(2) = 50 Гц. 3.16 Электродвигатели В электродвигателях явление электромагнитной индукции используется для обратного преобразования электрической энергии в механическую. Если по рамке, помещенной в магнитное поле B, пропускать переменный электрический ток I, то на нее со стороны магнитного поля будет действовать вращательный механический момент M [ pm B] где pm ISn - магнитный момент рамки, S – площадь рамки. В результате рамка будет вращаться с частотой, равной частоте переменного тока .




