Тарификация российского рынка ОСАГО на

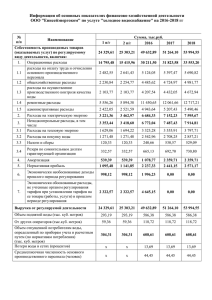
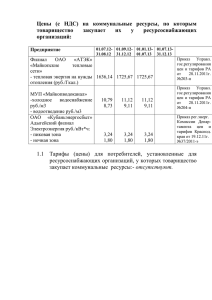
НЕЗАВИСИМЫЙ
АКТУАРНЫЙ ИНФОРМАЦИОННОАНАЛИТИЧЕСКИЙ
ЦЕНТР
Тарификация российского рынка ОСАГО на основе обобщенной
линейной модели
Селиванова Анна, актуарий
Москва, май 2008 г.
1
Содержание:
Применение обобщенной линейной модели для
расчета тарифов ОСАГО;
Особенности сбора статистических данных ОСАГО;
I.
II.


Анализ модели
III.


IV.
2
структура данных, представленных для анализа;
сделанные предположения с учетом особенностей статистики;
чувствительность модели к закону распределения убытка;
анализ влияния специфики сбора данных на оценки тарифов
ОСАГО;
Сравнение результатов, полученных с использованием
однофакторной и многофакторной моделей
Процедура расчета страховых тарифов
Основные предположения методики расчета тарифов,
основанной на обобщенной линейной модели

количество страховых случаев в каждой тарифной ячейке имеет
пуассоновское распределение П(λ);

распределение убытков по каждой тарифной ячейке имеет гамма
распределение Г(μ,φ);

параметры λ , μ мультипликативно зависят от уровней факторов
риска, определяющих ячейки рынка автострахования:
i , j ,... k  base  f1 j   f 2 j   ...  f nk 
3
 i , j ,.. k   base  f1i   f 2i   ...  f nk 
Особенности сбора статистических данных
Базовые уровни факторов риска
4
Фактор
Используется для
типа ТС
Базовый уровень
Тип
используемых
данных
Число
уровней
Собственник ТС
Легковые
автомобили
Физическое лицо
не объединенные
2
Территория
Все типы ТС
Населенные пункты с
территориальным
коэффициентом КТ=1
не объединенные
7
Возраст и стаж
Все типы ТС, кроме
прицепов
От 22 лет и старше со стажем
вождения свыше 2 лет
объединенные
4
Ограничение на число
лиц, допущенных к
управлению ТС
Все типы ТС, кроме
прицепов
Договор предусматривает
ограничение
объединенные
2
Мощность
Легковые
автомобили, такси
Свыше 70 до 95 л.с.
включительно
не объединенные
7
Период использования
Все типы ТС
Более 9 месяцев
объединенные
5
Анализ модели
Чувствительность модели к закону распределения
убытка;
I.




II.
5
гамма;
логарифмически – нормальное;
равномерное;
смесь двух гамма – распределений;
Чувствительность модели к специфике сбора
данных.
Чувствительность к закону распределения убытка
25
25
20
20
Гамма -распределение
Гамма -распределение
Логнормальное распределние
Равномерное распределение
15
%
%
15
10
10
5
5
0
0
24950 24958 24965 24973 24980 24988 24995 25003 25010 25018 25025 25033 25040 25048 25055 25063 25070 25078
Распределение
25
Средний размер выплат
Гамма -распределение
25 000.18
Логнормальное распределение
25 000.30
24950 24958 24965 24973 24980 24988 24995 25003 25010 25018 25025 25033 25040 25048 25055 25063 25070 25078
20
Гамма -распределение
Смесь Гамма- распределений
15
25 008.35
Равномерное распределение
25 000.52
%
Смесь Гамма- распределений
10
5
0
6
24950 24958 24965 24973 24980 24988 24995 25003 25010 25018 25025 25033 25040 25048 25055 25063 25070 25078
Чувствительность к закону распределения убытка
Гамма распределение
Смесь Гамма-распределений
Отклонение среднего размера убытка в базовой
ячейке, распределенного по гамма-распределению и
смеси гамма- распределений от истинного значения
с доверительными интервалами
0
0
-30
-20
-10
0
10
20
30
40
Отклонение коэффициентов страховых тарифов от
истинных значений с доверительными интервалами
для двух распределений: гамма-распределения и
смеси гамма- распределений
-0.03
7
-0.02
-0.01
0
0.01
0.02
0.03
Гамма
Смесь Гамма
КТ 1
КТ 1
КТ 2
КТ 2
КТ 3
КТ 3
КТ 4
КТ 4
КТ 5
КТ 5
КТ 6
КТ 6
КМ1
КМ1
КМ2
КМ2
КМ3
КМ3
КМ4
КМ4
КМ5
КМ5
Чувствительность к специфике исходных данных
I модель
Мощность Территория
x
II модель
Возраст и стаж
Мощность Территория
x
Возраст и стаж
x
GENMOD
GENMOD
GENMOD
Коэффициенты страховых тарифов
8
Коэффициенты страховых тарифов
Чувствительность к специфике исходных данных
0
-2
Модель: 3 фактора
Модель: 2+1 фактор
КТ 1
КТ 1
КТ 2
КТ 2
КТ 3
КТ 3
КТ 4
КТ 4
КТ 5
КТ 5
КТ 6
КТ 6
КМ1
КМ1
КМ2
КМ2
КМ3
КМ3
КМ4
КМ4
КМ5
КМ5
КВС1
КВС1
КВС2
КВС2
КВС3
КВС3
-1.5
-1
-0.5
0
0.5
1
1.5
2
Отклонение среднего размера убытка в базовой ячейке, рассчитанного по
полной и усеченной модели
9
Чувствительность к специфике исходных данных
Отклонение оценок среднего
размера выплат для базовой
ячейки от заданных значений,
рассчитанные по 2 вариантам
0
-150
-100
-50
Модель: 2+1 фактор
0
50
100
Модель: 3 фактора
Отклонение оценок частоты для
базовой ячейки от заданных
значений, рассчитанные по 2
вариантам
0
-0.003
-0.002
-0.001
0
Модель: 3 фактора
10
0.001
0.002
0.003
0.004
0.005
Модель: 2+1 фактор
0.006
Сравнение результатов однофакторной и
многофакторной модели
Типы ТС
11
Отношение суммарных выплат к премии
Многофакторная модель
Однофакторная модель
Легковые а/м физ. лица
1.00
0.92
Легковые а/м юр. лица
1.01
0.93
Прицепы к легковым а/м
1.00
1.08
Такси
0.98
0.79
Грузовые а/м до 16 т
1.01
1.08
Грузовые а/м свыше 16 т
1.02
1.29
Прицепы к грузовым а/м
1.00
1.04
Автобусы до 20 мест
1.00
1.02
Автобусы свыше 20 мест
1.00
1.08
Троллейбусы
1.00
0.91
Трамваи
1.00
0.92
Тракторы
1.00
1.00
Мотоциклы и мотороллеры
1.01
0.87
Все типы ТС
1.00
0.95
Сравнение результатов однофакторной и
многофакторной модели
Отношение суммарных выплат к премии
12
КТ
Многофакторная
модель
Однофакторная модель
КТ = 2
1.00
0.86
КТ = 1.8
1.00
0.91
КТ = 1.7
1.00
0.93
КТ = 1.6
1.01
0.99
КТ = 1.3
1.00
0.93
КТ = 1
1.00
0.96
КТ = 0.5
1.00
1.06
Все территории
1.00
0.95
Выводы

Оценка страховых тарифов для российского рынка ОСАГО, построенная
на основе ОЛМ (GenMod), достаточно устойчива к возможным
отклонениям закона распределения убытков от базисных предположений.

Использование для расчета тарифов ОЛМ (GenMod), в которой
одновременно включены не все исследуемые факторы тарификации,
может привести к существенному смещению оценок, как для поправочных
коэффициентов, так и для среднего размера убытка и частоты страхового
случая в базовой ячейке в том случае, если факторы тарификации
сильно коррелируют между собой. Как следствие этого, оценка для
премии также будет смещенной от истинного значения.
13
Выводы

Использование более простых однофакторных моделей вместо
многофакторных для оценки страховых тарифов может в конечном счете
существенно сказаться на убыточности страховой компании (как в случае
добровольного, так и в случае обязательного страхования).

Применение ОЛМ и детализированных статистических данных,
полностью соответствующих требованиям модели, позволяет не только
рассчитать адекватные рынку тарифы, но также проводить анализ
убыточных сегментов рынка для принятия бизнес решений.
14
Контактная информация
НЕЗАВИСИМЫЙ
АКТУАРНЫЙ ИНФОРМАЦИОННОАНАЛИТИЧЕСКИЙ
ЦЕНТР
Адрес: 125284, Москва, 1-й Хорошевский проезд, 3А
тел.: +7 (495) 255-63-08, +7 (495) 945-41-31
Адрес в Интернете: www.iaac.ru
e-mail: Chief@Actuaries.ru
15