Документ 472271

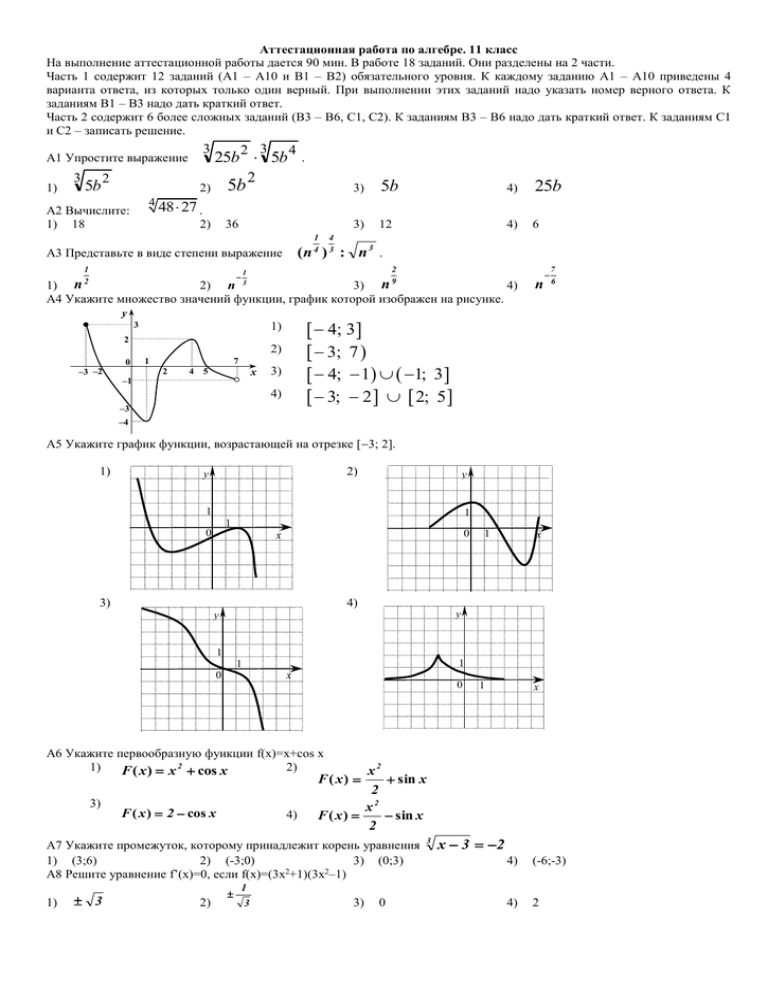
Аттестационная работа по алгебре. 11 класс
На выполнение аттестационной работы дается 90 мин. В работе 18 заданий. Они разделены на 2 части.
Часть 1 содержит 12 заданий (А1 – А10 и В1 – В2) обязательного уровня. К каждому заданию А1 – А10 приведены 4
варианта ответа, из которых только один верный. При выполнении этих заданий надо указать номер верного ответа. К
заданиям В1 – В3 надо дать краткий ответ.
Часть 2 содержит 6 более сложных заданий (В3 – В6, С1, С2). К заданиям В3 – В6 надо дать краткий ответ. К заданиям С1
и С2 – записать решение.
3
А1 Упростите выражение
1)
3
5b
2
2 3
25b  5b
А2 Вычислите:
1) 18
.
5b 2
2)
4
4
3)
5b
4)
25b
3)
12
4)
6
48  27 .
2)
36
1
4
(n ) : n 3 .
А3 Представьте в виде степени выражение
1
2
4
3
2
9
1
3

1) n
2) n
3) n
4)
А4 Укажите множество значений функции, график которой изображен на рисунке.
y
3
2)
–3 –2
–1
1
7
2
x
4 5
7
6
  4; 3
  3; 7 
  4;  1   1; 3 
  3;  2    2; 5 
1)
2
0
n

3)
4)
–3
–4
А5 Укажите график функции, возрастающей на отрезке [3; 2].
1)
2)
y
y
1
1
1
0
0
x
3)
1
x
4)
y
y
1
1
1
0
x
0
1
x
А6 Укажите первообразную функции f(x)=x+cos x
1)
2)
F ( x )  x 2  cos x
x2
 sin x
2
x2
F ( x) 
 sin x
2
F ( x) 
3)
F ( x )  2  cos x
4)
А7 Укажите промежуток, которому принадлежит корень уравнения
1) (3;6)
2) (-3;0)
3) (0;3)
А8 Решите уравнение f’(x)=0, если f(x)=(3x2+1)(3x2–1)
1)
 3
2)

3
x  3  2
4)
(-6;-3)
4)
2
1
3
3)
0
А9 На рисунке изображен график функции
y  f  x  . Какому из следующих промежутков
y
принадлежит точка максимума функции?
1)
3)
1
(– 4; –2)
(– 3; 0)
2)
4)
1
(5; 7)
(0; 3)
А10 Вычислите значение производной функции у = sin x – 2х
1)
–3
2)
1
x
0
в точке х0 = 0.
–1
3)
4)
0
2 х  37  x  1.
В1 Решите уравнение
В2 Функция у = f(x) определена на промежутке (– 6; 4). График ее производной
изображен на рисунке. Укажите точку минимума функции у = f(x) на этом
промежутке.
у
у = f (x)
1
–6
В3 Укажите наименьшее натуральное решение неравенства
В4 Вычислите площадь фигуры, ограниченной линиями
В5 Укажите абсциссу точки графика функции
нулю.
 х  2 4 х  3
х4
С1 Известно, что
c c
с 1
1
2

с

1
2
1 с
С2 Решите неравенство x -2x<x.
2
1

1
. Найдите с.
28
4
х
 0.
2
2
, в которой угловой коэффициент касательной равен
В6 Найдите решение (x0; y0) системы уравнений и вычислите значение суммы x0+y0:

1
у  х  1; х  1; х  4 , y=0.
f ( x)  5  4 x  x

 x2 y 4


2 x  y  3
0