Гильбертов куб иньективно универсальный объект в классе метрических компактов.
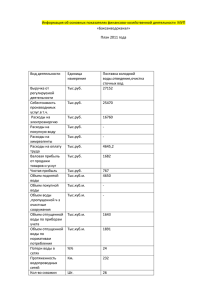
реклама

Гильбертов куб
(гильбертов кирпич, параллелепипед,…) -
иньективно универсальный объект в
классе метрических компактов.
П. В. Семенов,
.
Дубна, 22 июля 2015
Гильбертов куб -1
Имеются три модели (варианта определения)
Q1. Множество всех последовательностей чисел из
отрезка [0; 1] (иногда [-1; 1]). Расстояние:
d (( x1 , x2 , x3 ,...); (y1 , y 2 , y3 ,...)) x1 y1
x2 y2
2
x3 y3
4
... 2
Q2. Подмножество гильбертова пространства
(квадратично суммируемых последовательностей),
состоящее из тех векторов, у которых n-я координата
принадлежит отрезку [0;1/n]. Расстояние (евклидово):
(( x1 , x2 , x3 ,...); (y1 , y2 , y3 ,...)) (x1 y1 ) (x 2 y 2 ) (x 3 y3 ) ...
6
2
2
2
Q3. Декартово произведение [0; 1] х [0; 1] х [0; 1] х…
с (тихоновской) топологией.
Гильбертов куб -2
Счетное число попарно перпендикулярных базисных
векторов. Длина (=расстояние до (0,0,0,…))
первого = 1, длина второго = ½, третьего = ¼, …..
Гильбертов куб -3
Гильбертов куб Q содержит все конечномерные кубы
[0; 1],
[0; 1] х [0; 1],
[0; 1] х [0; 1] х [0; 1], …
и значит содержит (гомотетичные) копии всех компактов
лежащих на прямой, на плоскости, в пространстве,…
Оказывается, что гильбертов куб Q содержит
(гомеоморфные) копии вообще всех метрических
компактов.
Теорема. Для любого метрического компакта Х
найдется подкомпакт X ' Q и гомеоморфизм
h
(=непрерывная в обе стороны биекция) X
X '
h1
h
1
X
Y
,
h
непрерывно
?
?
h
гомеоморфизм
(
h
непрерывно)
h 1
Ответ: нет, но да для компактного Х,
тогда к тому же Y = h(X) будет компактом.
Гильбертов куб -4
Ф1. (Топология поточечной сходимости.)
An A0 An сходится к А0 покоординатно
Док-во. , а трив
n
0
x
x
k
k
1
1
j
j
d (A n ; A0 ) j 1 j 1 j 1... j k 1... j 1 j 1 k 1
2
2
2
Ф2. У Q – континуум «вершин». Точнее, множество
вершин биективно (и гомеоморфно) КМ К.
Док-во.
Множество «вершин» – это множество всех
последовательностей из 0 и 1. Биективность очевидна, а
непрерывность – из-за поточечной сходимости.
! В любой окрестности любой вершины есть еще вершины
101111…, 100111…., 10001111…., ….. 10000….
Гильбертов куб -5
Ф3. Множество всех граней всюду плотно в Q (в любой
окрестности любой точки есть точки из граней).
Док-во.
1
d (( x1 , x2 ,..., xn , x n 1 ,...); ( x1 , x2 ,..., xn , 0, 0, 0...)) n
2
Множество всех последовательностей чисел из (0; 1) –
псевдовнутренность P гильбертова куба Q.
Ф4. Q – компакт
(Б-В: в любой последовательности есть сход. под-ть)
Док-во. В модели Q3 – теорема Тихонова. В модели Q2 –
полнота гильбертова пространства + замкнутость Q +
наличие конечных сетей.
Гильбертов куб -6
Док-во. В модели Q1 – через Б-В для отрезка.
A1 Q
опр
A2 Q
A3 Q
опр
опр
... ? выбрать сход. подп ть
...
x11
x12
x13
...
числа из [0;1]
x12
x22
x23
...
числа из [0;1]
x31
x32
x33
...
числа из [0;1]
...
x10- первую координату нужного предела
1) Чтобы найти
применим Б-В к последовательности первых координат
x1n1 , x1m2 , x1m3 ,.... x10 [0;1]
An ;
а в качестве первого члена сход.подп-ти возьмем
Все остальные точки будут выбираться из мест
m2 , m3 , m4 ,...
и сходимость первых координат сохранится
1
Гильбертов куб -7
0
x
2) Чтобы найти 2 - вторую координату нужного предела
применим Б-В к последовательности вторых координат
точек подпоследовательности, выбранной на шаге 1)
x2m2 , x2m3 , x2m4 ,.... x2n2 , x2p3 , x2p4 ,.... x20 [0;1]
а в качестве второго члена сход.подп-ти возьмем An ; при
этом в первых координатах мы «перешли» к под-ти, от
чего сходимость к x10 сохранится.
3) Далее аналогично,
2
x3p3 , x3p4 , x3p5 ,.... x3n3 , x3s4 , x3s5 ,.... x30 [0;1]
и т.д. Получим точку A0 Q и подп-ть An , An , An ,......
которая сходится к A0 поточечно и, значит, сходится в Q.
1
2
3
Гильбертов куб -8
Ф 5. Декартово произведение счетного числа
метрических компактов – метрический компакт.
Док-во. Уже.
Ф 6. Q – непрерывный образ К.
Док-во.
Множество натуральных индексов 1,2,3,4,… разобьем на
попарно непересекающиеся бесконечные подмножества.
Каждая точка из К, т.е. последовательность из 0 и 2 задаст
тогда счетное число последовательностей из 0 и 2, т.е.
последовательность элементов из К.
Это биекция и непрерывность проверяется. Значит,
K
h
1
h
K
"на"
[0;1]
K
K
...
"на"
"на" ....
[0;1] [0;1] ..... Q
Гильбертов куб -9
Док-во теоремы об универсальности.
Сначала повторим то, что было в «КМ»
Для любого 0 в метрическом компакте ( X , ) есть
конечная сеть. Строим конечные сети для
1, 1/ 2, 1/ 3,.... . Выписываем поочередно все сети
друг за другом. Получаем последовательность {s1 ,s2 ,...}
плотную в X. Можно считать, что всегда (x, y) 1
Отображение h : X Q определяем равенством
h( x) ( x, s1 ), ( x, s2 ), ( x, s3 ),....
Если x y, то есть точка sn , которая к х ближе, чем к y.
Тогда n-е координаты h(x) и h(y) – разные, т.е. h- иньекция
h
X ' . Покоординатная непр-ть:
X
Если h( X ) X ', то
h
( x; sn ) ( y; sn ) ( x; y). Значит, h – непрерывно и
X' - компакт. Поэтому и h 1 непрерывно.
1
Гильбертов куб -10
У гильбертова куба есть свойства похожие на свойства
конечномерных кубов, но есть и совсем не похожие.
Например, все выпуклые компакты на прямой – отрезки,
все выпуклые компакты на плоскости (в пространстве,…)
гомеоморфны квадрату (трехмерному кубу,….)
Теорема Келлера (1931) Любой бесконечномерный
выпуклый компакт в гильбертовом пространстве
гомеоморфен Q.
Факт удивительный и сложный: нет никакой «почти
гомотетии» так как нет внутренних точек
Гильбертов куб -11
Гомеоморфизм пространства на себя – автогомеоморфизм
При автогомеоморфизме конечномерного куба внутренние
точки переходят во внутренние, а граничные - в граничные.
h
[0;1] , 0 h(0) 1
Например, от противного, пусть [0;1]
1
h
гомеом
Тогда h : (0;1] [0;1] \{h(0)}, но слева множество связное,
а справа – нет.
Для больших размерностей – гомотопические группы…..
Итак, конечномерные кубы топологически неоднородны.
А вот Q – топологически однороден: локально между его
точками нет «никакой разницы».
Теорема Для любых двух точек гильбертова куба
существует автогомеоморфизм куба, переводящий одну
точку в другую.
Mix
Если Х – бесконечный компакт, то множество Р(Х)
всех вероятностный мер на Х (с «интегральной»
метрикой) гомеоморфно Q.
Если Х – пеановский континуум (=непрерывный
образ отрезка), то его компактная экспонента expX
(множество всех подкомпактов) гомеоморфно Q.
Всякое компактное
гомеоморфно Q.
стягиваемое
Q-многообразие
Спасибо за внимание.