Геометрическая алгебра и понятие бесконечности

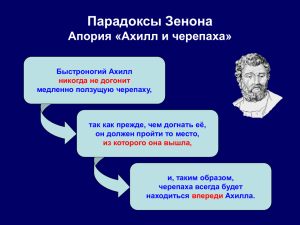
ОГОУ СПО «БИТ»
Геометрическая алгебра
и понятие бесконечности
Подготовил:
студент 16К группы
Щербаков Денис
Преподаватель: Горячева А.О.
2011 – 2012 уч. г.
Математика в древности
В странах-современниках
Эллады математика
использовалась
• либо для обыденных нужд
(подсчёты, измерения),
• либо, наоборот, для
магических ритуалов, имевших
целью выяснить волю богов
(астрология, нумерология
и т. п.).
Греки считали:
• «Числа правят миром»
или
• «Природа разговаривает с
нами на языке математики».
Вавилоняне
• рассматривали, для наглядности, неизвестные числа
как длину линии или площадь фигуры, но
последние всё же всегда оставались числами.
• Это проявлялось уже в том, что с неизвестными
величинами, по названию имеющими различные
измерения, обращались как с однородными:
“площадь” складывали со “стороной”, от “объема”
отнимали “площадь”
Вавилоняне
• при решении уравнений с двумя неизвестными,
одно неизвестное называли “длиной”, другое ”шириной”.
• произведение неизвестных называли “площадью”.
• в задачах, приводящих к кубическому уравнению,
встречалась третья неизвестная величина “глубина”, а произведение трех неизвестных
именовали “объемом”.
Геометрическая алгебра
• В Древней Греции пифагорейцы
открыли несоизмеримые величины,
чертежи из средства наглядности
превратились в основной элемент
алгебры. Чертежи стали основным
элементом алгебры.
Евклид
• Результаты такого подхода нашли
отражение во второй книге “Начал”
Евклид. Новое исчисление
получило впоследствии название
“геометрической алгебры”.
Геометрическая алгебра
• В этом исчислении величины стали изображаться с
помощью отрезков и прямоугольников, а любые
утверждения и доказательства имели право на
существование только в том случае, если они давались на
геометрическом языке.
• Древнегреческие математики работали не с числами, а с
отрезками. Поэтому найти неизвестное для них означало
построить искомый отрезок.
• В геометрической алгебре величины стали изображать с
помощью отрезков и прямоугольников.
Геометрическая алгебра
• Сложение отрезков осуществлялось путем
приставления одного из них к другому вдоль
прямой.
b
a
a
+
b
Геометрическая алгебра
• Вычитание - путем отсечения от большего
отрезка части, равной меньшему отрезку.
b
a
a-b
Геометрическая алгебра
• Умножение осуществлялось путем
построения прямоугольника на
соответствующих отрезках.
b
a
a*b
Геометрическая алгебра
• Деление приводило к понижению
размерности и выполнялось с помощью все
того же “приложения площадей”.
Найти ab : с
Доказательство распределительного
(дистрибутивного) закона умножения
ab = (a1+a2+…+an)b = a1b+a2b+…anb
a
b
a1
…
an
Доказательство тождества
(a+b)2 = a2+2ab+b2
a
a2
b
ab
b ab
b2
a
Задачи о «приложении площадей»
1) преобразовать данный прямоугольник в квадрат,
т.е. решить уравнение x2=ab (параболическая
задача);
2) приложить к данному отрезку а прямоугольник
заданной площади S так, чтобы «недостаток» был
квадратом: x(a-x)=S (эллиптическая задача);
3) приложить к данному отрезку а прямоугольник
заданной площади S так, чтобы «избыток» был
квадратом: x(a+x)=S (гиперболическая задача);
Задачи о «приложении площадей»
• С помощью циркуля и линейки можно
решать задачи, эквивалентные квадратным
уравнениям, имеющим действительный
положительный корень.
Задачи о «приложении площадей»
Очень скоро появились и другие задачи:
• об удвоении куба,
2V
V
• о трисекции угла,
• о квадратуре круга.
S
S
Зенон Элейский
•
•
•
•
Самые известные
апории Зенона:
«Дихотомия»
«Ахиллес и черепаха»
«Стрела»
«Стадион»
Апории Зенона
Дихотомия (рассечение пополам).
• Движущееся тело никогда не достигнет конца
пути, поскольку сначала оно должно дойти
до середины пути, потом – до середины
остатка и так далее. Значит, прежде чем
дойти до конца, оно должно «отсчитать»
бесконечное число середин, а следовательно,
до конца дойти ему не удастся.
Апории Зенона
Ахиллес и черепаха.
• Быстроногий Ахиллес никогда не догонит
черепаху, если даст ей хотя бы маленькую
фору. Ведь пока он пробежит расстояние
форы, черепаха уползет на другое
расстояние, и пока Ахиллес добежит до того
места, она уползет еще дальше, и так до
бесконечности.
Спор Зенона и Диогена
Движенья нет, сказал мудрец брадатый.
Другой смолчал и стал пред ним ходить.
Сильнее бы не мог он возразить;
Хвалили все ответ замысловатый.
Но, господа, забавный случай сей
Другой пример на память мне приводит:
Ведь каждый день пред нами солнце ходит,
Однако ж прав упрямый Галилей.
А.С. Пушкин
Своим апориям Зенон придал ярко
выраженный физический смысл: он направил их
против возможности движения. Но ведь движение
тел происходит ежедневно на наших глазах! В чём
же дело?
Понятие бесконечности в древней
математике
• В Древней Греции развитие математики
протекало в сотрудничестве с
философией. Идея бесконечности
возникла в связи с представлениями о
Вселенной.
• В сочинении «О природе» Анаксагор
(около 500 – 428 гг. до н. э.), в котором он
вводит понятие бесконечности, говорит
так: «Среди малых величин не существует
наименьшей, но уменьшение идет
непрерывно. Всегда имеется нечто
большее, чем то, что большее».
Анаксагор
Анаксагор (V в. до н. э.)
В сочинении «О природе»
провозгласил, что «в малом не
существует наименьшего, но
всегда есть ещё меньшее».
В результате деления
отрезка всегда будут
получаться отрезки, которые
по-прежнему остаются
делимыми величинами, и таким
путём мы никогда не дойдём до
неделимых частиц.
Это означает, что отрезок
не состоит из точек, а есть
«геометрическое место» точек.